Книга: Песни о Паскале
Глава 47 Системы счисления
Разделы на этой странице:
- Из тьмы веков
- Число и его изображение
- Рис.103 – Способы изображения числа 12
- Десятичная система
- Рис.104 – Выделение отдельных цифр десятичного числа
- Рис.105 – Сборка числа из строки десятичных цифр
- Двоичная система
- Рис.106 – Изображение числа 12 в двоичной системе
- Шестнадцатеричная система
- Рис.107 – Преобразование двоичного числа в шестнадцатеричное
- Другие системы счисления
- Изображение числа в заданной системе счисления
- Обратное преобразование
- Итоги
- А слабо?
Глава 47
Системы счисления

Эта глава промчит нас дорогой, по которой человечество брело несколько тысячелетий, – мы научимся изображать числа.
Из тьмы веков
Когда явилась потребность в счете? – никто не помнит этого, но мудрецы всех времен упорно искали удобные способы изображения чисел. Поиск систем счисления – так их теперь называют – это захватывающая история! Трудно поверить, но античные математики ещё не знали десятичной системы! И как они решали свои замысловатые задачи?
Первой системой счисления была, очевидно, единичная. Тогда некоторому количеству одних предметов сопоставляли такое же количество других (камушков, ракушек или зарубок на дереве). Что тут скажешь? – каменный век! Изображать большие числа в этой системе немыслимо.
Потребовались века, чтобы индийцы додумались до цифр. Их цифры были похожи на современные «1», «2», «3» и так далее. Но истинную революцию в арифметике содеяла цифра «0». Тот, кто её придумал, поставил все на свои места, причем в буквальном смысле. Ведь ноль породил позиционную десятичную систему счисления, где «вес» цифры определяется её позицией внутри числа. Странно, что в просвещенной Европе удобная десятичная система приживалась непросто и вытеснила неудобную римскую только в 15-16 веках!
Наконец пробил час немецкого математика Лейбница, в голову которого пришла здравая мысль: «Зачем так много цифр? – изумился он, взглянув на циферблат своих часов, – когда вполне достаточно двух!». Так была изобретена двоичная система счисления, – «родная» для нынешних компьютеров.
Число и его изображение
Пора прояснить, что же такое системы счисления? Числа – это плод нашего воображения, в природе их никто не видел, они существуют лишь в наших головах. Не потому ли с числами связаны порой курьезные заблуждения? Иные полагают, что перевод числа из одной системы счисления в другую меняет это число. Вам смешно? Взгляните на рис. 103, где устроилась дюжина попугаев. Дюжина – это двенадцать, я написал это по-русски, а мог бы на другом языке. Или обозначил бы китайским иероглифом, – количество попугаев от этого не изменится. Как в поговорке: хоть горшком назови, только в печь не сажай!
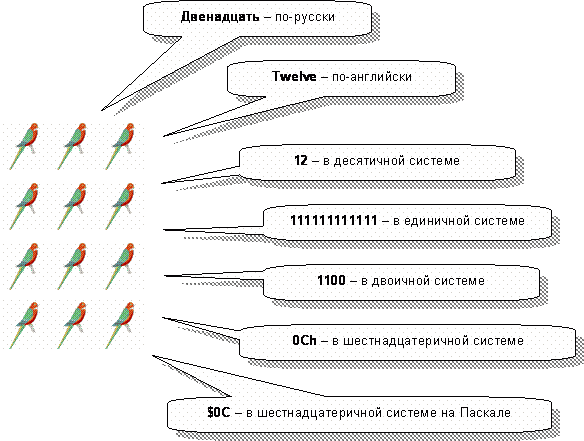
Рис.103 – Способы изображения числа 12
Итак, что ни скажи, но на картинке все те же двенадцать попугаев. Это число изображено рядом в нескольких системах счисления: единичной, десятичной, двоичной и шестнадцатеричной. И, хотя изображения не схожи меж собой, все они относятся к двенадцати попугаям. Стало быть, число и его изображение – не одно и то же!
Мы изображаем числа строками символов – цифрами. Поручив процедуре Writeln напечатать число, мы не задумываемся, как она делает это, – число превращается в строку цифр неведомым нам образом. Допустим на минуту, что процедура Writeln этого не умеет, и тогда явится потребность сделать такое преобразование самим. Итак, ставим себе первую задачу: преобразовать число в строку, то есть получить символьное изображение числа.
Справившись с первой задачей, займемся обратным преобразованием – строки в число. Это умеет процедура Readln, но мы пока забудем об этом. Дело в том, что упомянутые стандартные процедуры понимают лишь десятичную систему счисления. Мы же добиваемся большего, – мы хотим изображать числа в любой системе счисления (двоичной, троичной и так далее). А начнем, разумеется, с родной десятичной системы.
Десятичная система
Десятичную систему знает всякий: здесь крайняя правая цифра числа означает единицы, а последующие – десятки, сотни и так далее. Например, число 2048 представляется так:
2048 = 2 • 1000 + 0 • 100 + 4 • 10 + 8 • 1
Или так:
2048 = 2 • 103 + 0 • 102 + 4 • 101 + 8 • 100
То есть, позиция цифры в числе равна показателю степени при десятке, если счет позиций вести справа налево, начиная с нуля.
Повторю нашу цель: мы хотим превратить нечто цельное – число – в цепочку символов. Как это сделать? Есть мысли? Я предлагаю «откалывать» от числа цифру за цифрой, превращая их в символы и складывая в строку. Из опыта известно, что легче всего «отгрызть» от числа младшую цифру, вычисляя остаток от деления на десять, вот так:
младшая_цифра := число MOD 10
Тогда старшая часть числа отделится от младшей цифры делением на десять. При этом остаток будет отброшен, но он теперь и не нужен, поскольку сохранен в младшей цифре.
старшая_часть := число DIV 10
Так прояснилась схема дробления числа, показанная на рис. 104.
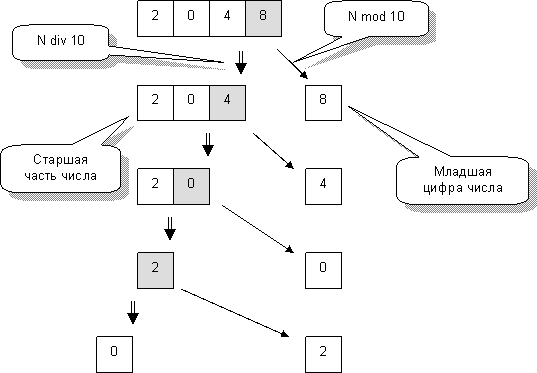
Рис.104 – Выделение отдельных цифр десятичного числа
Число дробится, пока в старшей части не окажется ноль. Осталось лишь организовать цикл, условием выхода из которого будет равенство нулю старшей части. Эта несложная программа перед вами.
var N : integer; S : string;
begin { Преобразование числа в строку десятичных цифр }
Write('N= '); Readln(N);
S:='';
repeat
S:= Char((N mod 10)+Ord('0')) + S; { выделение очередной цифры }
N:= N div 10; { отделение старшей части }
until N=0;
Writeln(S); Readln;
end.
Теперь, когда мы смогли превратить число в строку, займемся обратным превращением – соберем число из символов строки. Откуда подступиться к этой сборке? Запишем разложение числа с помощью скобок следующим образом:
2048 = 2 • 1000 + 0 • 100 + 4 • 10 + 8 • 1 = (((0 •10+2) •10+0) •10+4) •10+8
Правила действий со скобками требуют начать вычисление с внутренних, самых глубоких скобок. Следовательно, сборку числа из отдельных цифр начнем со старших разрядов, последовательно умножая накопленную сумму на 10. Внутри самых глубоких скобок добавлено слагаемое 0•10. Не влияя на результат вычислений, оно придает общность алгоритму сборки, который показан на рис. 105.
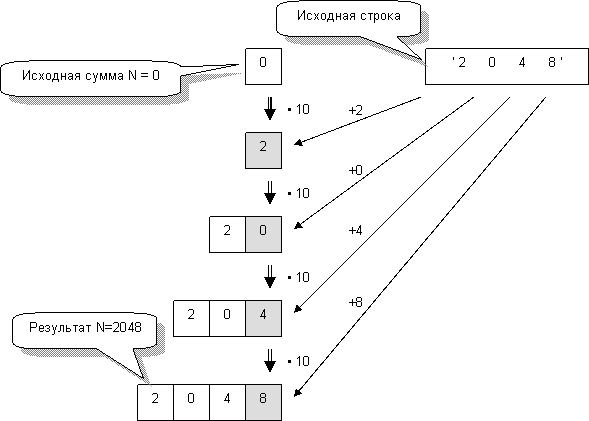
Рис.105 – Сборка числа из строки десятичных цифр
Например, для числа 2048 сборка пойдет в таком порядке:
N = 0 – исходное значение
N = 0 • 10 + 2 = 2
N = 2 • 10 + 0 = 20
N = 20 • 10 + 4 = 204
N = 204 • 10 + 8 = 2048
А вот программа, работающая по этому алгоритму.
var N : integer; i : integer; S : string;
begin
Write('S= '); Readln(S);
N:=0;
for i:=1 to Length(S) do N:= 10*N + Ord(S[i]) – Ord ('0');
Writeln(N); Readln;
end.
Разобравшись со сборкой-разборкой десятичных чисел, замахнемся теперь на процедуры, пригодные для любых систем счисления. Но прежде ознакомимся с устройством этих систем.
Двоичная система
«Отец» двоичной системы Лейбниц не помышлял о великом будущем своей придумки, и на долгие годы о ней забыли. Но изобретатели компьютеров вспомнили. Все компьютеры – от первых моделей до самых современных – строятся из простейших элементов памяти – триггеров. Триггер – это электронная схема с двумя устойчивыми состояниями. Подобие триггера – комнатный выключатель, что может (если исправен) находиться в двух устойчивых состояниях: «включен» и «отключен». То есть, выключатель «помнит» состояние, в которое его привели в последний раз, и является элементом памяти.
Итак, элементы памяти с двумя состояниями – триггеры – составляют основу компьютеров (и почему их не назвали «дваггерами»?). Одно из состояний инженеры обозначили числом 0, а другое – 1. Стало быть, триггер способен «помнить» одно из этих чисел. Маловато для серьезного счета, не так ли? Тогда и вспомнили о двоичной системе Лейбница. Инженеры соединили несколько триггеров в цепочку и назвали эту «гирлянду» регистром. Каждый триггер в регистре, подобно цифрам в десятичном числе, обладает своим весом. В зависимости от позиции в регистре, вес триггера может составлять 1, 2, 4, 8 и так далее, – это степени числа 2. Например, число 12 изображается в двоичной системе так (рис. 106).
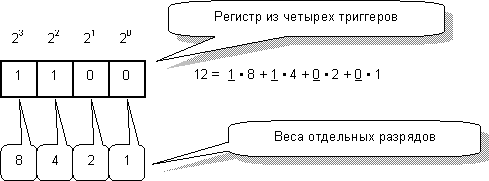
Рис.106 – Изображение числа 12 в двоичной системе
Сравните эту кодировку с десятичной системой, – принцип тот же, только веса разрядов другие. Если в десятичной системе вес очередного разряда вдесятеро больше предыдущего, то в двоичной системе – вдвое. Числа, хранящиеся в триггерах (0 или 1) служат множителями этих весов. Таким образом, при достаточной длине регистра в двоичной системе можно изобразить сколь угодно большое число.
Договоримся о форме записи двоичных чисел, иначе путаницы не избежать. У программистов приняты две формы: к символам двоичного изображения добавляют либо суффикс «B» (от Binary – «двоичный»), либо маленькую двоечку. Например, число 12 в двоичной системе записывается так:
1100B или 1100b или 11002
А иначе эту запись можно понять как «тысяча сто» в десятичной системе.
Шестнадцатеричная система
Компьютеры никогда не жаловались на двоичную систему, она их вполне устраивает. Сетовать стали программисты, – уж очень громоздкой получалась запись сравнительно небольших чисел, например:
4005 = 1111101001012
А если программистам несподручно, они что-нибудь придумают. Придумка была простой: двоичную запись разбили на группы по четыре двоичных цифры в каждой – тетрады (от греческого слова Tetra – «четыре»). И каждую тетраду записали в привычной для людей десятичной системе, разделяя тетрады точками. Например, десятичное число 4005 преобразили так:
4005 = 1111101001012 –> 1111.1010.01012 –> 15.10.05
Тетрады могут содержать числа от 0 до 15 – всего получается 16 значений, потому систему назвали шестнадцатеричной. Со временем запись сделали ещё короче, заменив числа от 10 до 15 буквами латинского алфавита:
A=10
B=11
C=12
D=13
E=14
F=15
Тогда показанная выше запись преобразилась так: 15.10.05 –> FA5
Рис. 107 показывает это наглядней.
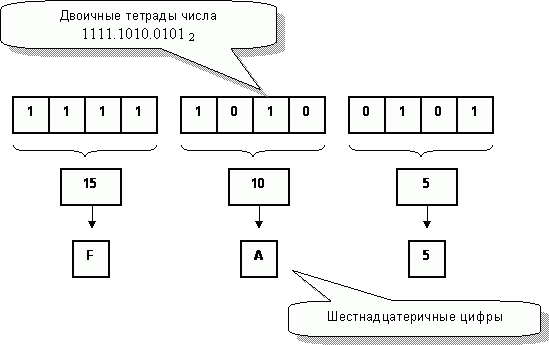
Рис.107 – Преобразование двоичного числа в шестнадцатеричное
Шестнадцатеричную запись можно спутать с десятичной, и даже принять за слово, поскольку в ней встречаются буквы. Потому для таких чисел учредили свои правила: шестнадцатеричная запись числа должна начинаться с цифры, а завершаться суффиксом «H» (от Hexadecimal, Hex – «шестнадцатеричный»). Значит, изобразить число FA5 правильней так:
0FA5H или 0FA5h
Применяют и другие формы записи шестнадцатеричных чисел. Так, в языке Си принята приставка «0x» (0xFA5), а в Паскале начинают с приставки «$» – это знак доллара ($FA5). В таких записях лидирующий ноль не требуется, но для лучшего восприятия указывают обычно две, четыре, либо восемь цифр (в зависимости от величины числа или разрядности данных), например:
12 = 0x0C = $0C <– байт (byte)
4005 = 0x0FA5 = $0FA5 <– слово (word)
4005 = 0x00000FA5 = $00000FA5 <– длинное слово (longint)
Чем хороша шестнадцатеричная система? Легкостью перевода чисел в двоичную систему и обратно. После небольшой тренировки любой может сделать это в уме. При переводе в двоичную систему заменяем каждую шестнадцатеричную цифру четырьмя двоичными и «склеиваем» эти тетрады между собой. И, хотя компьютеры по-прежнему работают в двоичной системе, программисты дружно перешли на шестнадцатеричную. Вот таблица для перевода небольших чисел из одной системы в другую.
Табл. 11 – Изображения чисел в различных системах счисления
| Десятичная | Двоичная | 16-ричная | Десятичная | Двоичная | 16-ричная |
| 0 | 0000 | 0 | 8 | 1000 | 8 |
| 1 | 0001 | 1 | 9 | 1001 | 9 |
| 2 | 0010 | 2 | 10 | 1010 | A |
| 3 | 0011 | 3 | 11 | 1011 | B |
| 4 | 0100 | 4 | 12 | 1100 | C |
| 5 | 0101 | 5 | 13 | 1101 | D |
| 6 | 0110 | 6 | 14 | 1110 | E |
| 7 | 0111 | 7 | 15 | 1111 | F |
Другие системы счисления
Итак, мы познакомились с тремя позиционными системами счислений: десятичной, двоичной и шестнадцатеричной. Существуют ли другие системы? Конечно! Во всех позиционных системах вес цифры определяется её положением в числе, сравните.
2048 = 2 • 103 + 0 • 102 + 4 • 101 + 8 • 100 - десятичная;
12 = 11002 = 1 • 23 + 1 • 22 + 0 • 21 + 0 • 10 - двоичная;
4000 = $FA0 = F • 162 + A • 161 + 0 • 160 - шестнадцатеричная.
Число, на котором построена система, называют её основанием. Можно выдумать столько систем счисления, сколько существует чисел, то есть, бесконечно много. Пока нам достаточно тех, что придуманы. А если с других планет прилетят существа с семью пальцами на руках? Для них, вероятно, «родной» будет семеричная система, и мы должны быть готовы к этому!
Так мы подошли к задаче по настоящему серьезной: изобразить число в некоторой системе счисления (основания систем ограничим числами от 2 до 16).
Изображение числа в заданной системе счисления
Преобразуя числа в десятичную систему, мы «отгрызали» цифры, начиная с младших разрядов, операциями деления и получения остатка. Точно так же преобразуют числа и в другие системы, только откалывают куски иного размера. Поскольку в двоичной системе есть только две цифры, то для неё младшая цифра отсекается операцией MOD 2, а старшая часть – операцией DIV 2. Для шестнадцатеричной системы – соответственно операциями MOD 16 и DIV 16. Отсюда следует правило: для преобразования числа в N–ричную систему счисления младшую цифру отделяют операцией MOD N, а старшую часть числа – операцией DIV N.
В программе «P_47_1» функция ConvertFromNumber – «преобразовать из числа» – делает именно то, о чем сказано выше. Обратите внимание на строковую константу.
const CDigits : string = '0123456789ABCDEF';
Она служит для изящного преобразования чисел 0–15 в шестнадцатеричные цифры «0»–«F». Константы, для которых явно указан тип, называют типизированными, – это пример такой константы.
{ P_47_1 – Преобразование в произвольную систему счисления }
{ Функция преобразования десятичного числа в другие системы счисления }
function ConvertFromNumber(aBase, aNumber : integer): string;
const CDigits : string = '0123456789ABCDEF';
var n : integer; c : char; S : string;
begin
S:=''; { Накопитель цифр }
repeat
n:= aNumber mod aBase; { остаток от деления на основание }
aNumber:= aNumber div aBase; { частное от деления на основание }
c:= CDigits[1+n]; { выбираем цифру из строки }
S:= c + S; { вставляем цифру в результат }
until aNumber=0;
ConvertFromNumber:= S; { готово! }
end;
var B, N : integer; { B – основание системы, N – число }
begin {=== Главная программа ===}
repeat
Write('Основание системы= '); Readln(B);
if B in [2..16] then begin
Write('Преобразуемое число= '); Readln(N);
Writeln(ConvertFromNumber(B, N));
end
until not (B in [2..16]);
end.
Эта простая программа подарит вам счастье наблюдать знакомые десятичные числа в экзотических системах счисления, например, в троичной или пятеричной.
Обратное преобразование
Теперь займемся обратной задачей: пусть дана строка символов, изображающая некое число в известной системе счисления; требуется преобразовать эту строку в число и напечатать в десятичной системе.
Сборка числа из десятичных цифр нами освоена. Она выполнялась умножением накопленной суммы на десять с прибавлением очередной цифры, начиная со старшей. Надо ли объяснять, что сборка в других системах выполняется точно так же? Только умножать будем не на десять, а на основание системы счисления. В следующей ниже программе сборка выполняется функцией ConvertToNumber – «преобразовать в число».
{ P_47_2 – Преобразование из других систем счисления }
function ConvertToNumber(aBase: integer; aNumber: string): integer;
var i,n, Sum : integer;
c : char;
begin
Sum:=0; { Накопитель результата }
for i:=1 to Length(aNumber) do begin
c:= Upcase(aNumber[i]);
if c in ['0'..'9']
then n:= Ord(c)-Ord('0') {0..9}
else n:= 10+Ord(c)-Ord('A'); {10..15}
Sum:= aBase*Sum + n; { Накопление суммы }
end;
ConvertToNumber:= Sum; { готово! }
end;
var B : integer; { Основание системы }
N : string; { Изображение числа в виде строки }
begin {=== Главная программа ===}
repeat
Write('Основание системы= '); Readln(B);
if B in [2..16] then begin
Write('Преобразуемое число= '); Readln(N);
Writeln(ConvertToNumber(B, N));
end
until not (B in [2..16]);
end.
Как обычно, здесь выделены операторы, стоящие внимания. Функция UpCase преобразует строчные латинские буквы в заглавные. Ведь шестнадцатеричные цифры от «A» до «F» могут быть введены пользователем в любом регистре, а последующие операторы преобразования цифры в число предполагают заглавные буквы – вот потому и понадобилась функция UpCase.
Теперь о превращении символов в числа. Цифры от «0» до «9» преобразуются вычитанием из кода цифры кода символа «0». Для цифр от «A» до «F» после вычитания кода буквы «A» к разности прибавляем число 10. Все сказанное относится к следующему условному оператору.
if c in ['0'..'9']
then n:= Ord(c)- Ord('0') {0..9}
else n:= 10 + Ord(c)- Ord('A'); {10..15}
Вот, пожалуй, и вся премудрость. Испытание этой программы убедит вас в том, что волшебства случаются не только в сказках!
Итоги
• Способ изображения чисел посредством знаков называется системой счисления.
• Одно и то же число может быть изображено в разных системах счисления.
• Все современные системы счисления – позиционные. Это значит, что вес цифры определяется позицией в числе.
• Преобразование числа в любую систему счисления (строку цифр) начинается с младших разрядов, а обратная сборка – со старших.
А слабо?
А) Напишите функцию для преобразования числа из одной системы счисления в другую. Функция должна принимать три параметра:
• строку в исходной системе счисления;
• основание исходной системы;
• основание конечной системы счисления.
Воспользуйтесь вызовами готовых функций ConvertToNumber и ConvertFromNumber.
Б) У программиста Ника была привычка запоминать сумму цифр в номерах автомобилей, попадавшихся ему на глаза. Однажды он стал свидетелем аварии, виновник которой скрылся. Ник сообщил полицейским только сумму цифр в номере нарушителя (сам номер Ник не помнил). Помогите полиции, и напишите программу, выводящую все трехзначные номера (от 001 до 999), сумма цифр которых равна N (значение N вводит пользователь).
В) Напишите функцию для представления чисел словами. Например, число 45 должно быть преобразовано в строку «сорок пять». Решайте задачу постепенно: сначала для однозначных и двузначных чисел, затем для более крупных. Или слабо?
Г) В романе «Евгений Онегин» есть такие строки: «Все предрассудки истребя, мы почитаем всех нулями, а единицами – себя». О какой системе счисления упомянул Александр Сергеевич?
Д) В функцию передаются три параметра: 1) число, 2) основание системы счисления, 3) символ цифры. Функция должна возвратить количество вхождений этой цифры в представление числа для указанной системы счисления.
Е) Напечатать все трехзначные числа, цифры которых (в десятичном представлении) различны, например: 123, 702.
Ж) Найти все шестизначные счастливые билеты. Счастливыми называют билеты, у которых сумма первых 3-х цифр равна сумме следующих 3-х. Например: 123 411. Напишите булеву функцию, определяющую «счастливость» билета.
З) В заморской стране обращались денежные купюры достоинством в 1, 2, 5, 10 и 25 пиастров. Напишите программу для кассового аппарата, определяющую наименьший набор купюр, необходимый для выдачи сдачи на указанную сумму. Например, для сдачи 33 пиастров программа напечатает: 25 + 5 + 2 + 1.
И) Программа шифрования текстового файла заменяет каждый символ двумя шестнадцатеричными цифрами его кода. Например, три символа ‘405’ заменяются на шесть символов ‘343035’. Символы разбивки строк не затрагиваются. Напишите программу для зашифровки и расшифровки файла по этой системе.
К) Чтобы усилить шифр предыдущей задачи, выполните вращение преобразованной строки на несколько позиций: влево – при зашифровке, и вправо – при расшифровке (смотрите задачи к главе 44).
Л) Напечатайте все числа, не превышающие 1000, такие, что делятся без остатка на каждую из своих цифр. Например: 24, 36, 184, 612. Определите количество таких чисел.
- Только для взрослых
- Детям до 16–ти
- Глава 1 Путь далек у нас с тобою…
- Глава 2 Вместо теории
- Глава 3 Консольный интерфейс
- Глава 4 Оружие – к бою!
- Глава 5 Программа номер один
- Глава 6 Подготовка к следующему штурму
- Глава 7 Развиваем успех
- Глава 8 Постоянные и переменные
- Глава 9 Переменные: продолжение знакомства
- Глава 10 Условный оператор
- Глава 11 Операторный блок
- Глава 12 Цикл с проверкой в конце
- Глава 13 Правда и кривда
- Глава 14 Дважды два – четыре
- Глава 15 Айда в Монте-Карло!
- Глава 16 Делу время, а потехе час
- Глава 17 И вновь за парту
- Глава 18 Аз, Буки
- Глава 19 Процедуры и функции: разделяй и властвуй
- Глава 20 Процедуры: первый опыт
- Глава 21 Отладка
- Глава 22 О передаче параметров
- Глава 23 Функции
- Глава 24 Криптография
- Глава 25 Текстовые файлы
- Глава 26 Я не читатель, – я писатель!
- Глава 27 Дайте кораблю минутный отдых!
- Глава 28 Редактор и справочная система
- Глава 29 Читайте по-новому
- Глава 30 Журнальная история
- Глава 31 Финал журнальной истории
- Глава 32 Порядковые типы данных
- Глава 33 Вещественные числа
- Глава 34 Структура программы
- Глава 35 Множества
- Глава 36 Множества в Паскале
- Глава 37 Ввод и вывод множеств
- Глава 38 Множества в «бою»
- Глава 39 Командная игра (массивы)
- Глава 40 Пристрелка на знакомых мишенях
- Глава 41 По порядку, становись!
- Глава 42 Кто ищет, тот всегда найдет
- Глава 43 Сортировка по-взрослому
- Глава 44 Строки
- Глава 45 Очереди и стеки
- Глава 46 Огромные числа
- Глава 47 Системы счисления
- Глава 48 Железная логика
- Глава 49 Сложные массивы
- Глава 50 Неспортивные рекорды (записи)
- Глава 51 Указатели в море памяти
- Глава 52 Динамические переменные
- Глава 53 Массив указателей
- Глава 54 Односвязные списки
- Глава 55 Слова, слова, слова…
- Глава 56 И снова очереди, и снова стеки…
- Глава 57 Графомания
- Глава 58 По графу шагом марш!
- Глава 59 Крупные проекты
- Глава 60 Мелкие хитрости
- Глава 61 «Кубики» программиста (ООП)
- Глава 62 Самое интересное только начинается!
- Приложение А Установка и настройка IDE Borland Pascal
- Приложение Б Консольная программа в среде Delphi
- Приложение В Особенности IDE Pascal ABCNet
- Приложение Г Зарезервированные слова
- Приложение Д Ошибки компиляции
- Приложение Е Ошибки исполнения
- Приложение Ж Директивы управления компиляцией
- Приложение З Назначение пунктов меню
- Приложение И Стандартная кодировка символов MS–DOS
- Приложение К Некоторые встроенные процедуры и функции
- Приложение Л Перечень программ
- Приложение М Пример олимпиадной задачи
- Библиография
- Содержание книги
- Популярные страницы
- 1.3. Системы счисления
- 2.2. Арифметические операции над числами, представленными в различных системах счисления
- СИСТЕМЫ СЧИСЛЕНИЯ
- 2.1. Системы счисления
- Пример 12-33. Перевод чисел из одной системы счисления в другую
- Другие основания системы счисления
- 5.18. Преобразование системы счисления
- Перевод в различные системы счисления
- Упражнения для самостоятельного выполнения
- Контрольные вопросы




