Книга: Песни о Паскале
Глава 35 Множества
Разделы на этой странице:
- В директорском кабинете
- Первым делом, первым делом – оцифровка
- Множества глазами математика
- Рис. 80 – Множества точек черного (B) и белого (W) кругов
- Рис. 81 – Объединение непересекающихся множеств G = B + W
- Рис.82 – Объединение пересекающихся множеств G < B + W
- Рис.83 – Пересечение множеств G = B * W
- Рис.84 – Вычитание множеств
- Рис.85 Надмножество (B) и подмножество (W)
- Числовые множества
- Рис.86 – Множества чисел
- Мощность множества, полные и неполные множества
- Итоги
- А слабо?
Глава 35
Множества

С малых лет я завидовал обладателям волшебных палочек, ковров-самолетов и прочих волшебных штучек! Смел ли я мечтать о таких игрушках? И вот познакомился с Паскалем… Мы приступаем к мощнейшим средствам этого языка – сложным типам данных. Овладейте ими, и мудреные задачи разрешатся сказочно просто!
В директорском кабинете
Редкий смельчак сунется в директорский кабинет. Но чтобы вникнуть в предстоящую задачу, нам надо тайно проникнуть к директору школы. Вот вам шапка-невидимка (ещё одна волшебная штуковина), вдохните глубже и ступайте на цыпочках за мной.
Мы находим усталого Семена Семеновича перед кипой исчерканных листков с фамилиями учеников. Чем озабочен директор? Сейчас объясню. В начале учебного года Семен Семенович распорядился, чтобы все ученики вступили в какой-либо кружок или спортивную секцию – по желанию. А теперь, спустя пару месяцев, он проверяет исполнение приказа. Директор намерен наказать тех, кто не исполнил распоряжения, и поощрить состоящих в нескольких кружках или секциях. Но, промучившись неделю со списками кружков, он готов уж отказаться от своей затеи, – задача не поместилась в директорской голове. Судите сами: ведь в школе двести пятьдесят учеников! Спасайте Семена Семеновича!
Первым делом, первым делом – оцифровка
Директорскую задачу поручим компьютеру, а тому сподручней орудовать с числами. Заменим фамилии учеников числами, назначив каждому ученику уникальный, несовпадающий с другими, номер. Переход от фамилий к номерам и обратно – простая задачка, её мы оставим Семену Семеновичу. Таким образом, наш входной файл со списками учеников будет содержать по одной строке для каждого кружка, где перечисляются через пробел номера учеников, состоящих в этом кружке. Вот пример входного файла для трех кружков.
2 11 4 13
9 17 12 11 3 5 18
14 2 13 15 20
Здесь в первый кружок записались 4 школьника, во второй – 7, а в третий – 5 учеников. Как видите, их номера перечислены в произвольном порядке, что затрудняет ручную обработку таких списков. От компьютера требуется выявить номера учеников (от 1 до 250), которых нет в таком файле. Хочется найти простое решение, а оно возможно лишь с применением нового для нас типа данных – множества.
Множества глазами математика
Слово «множество» намекает на большое количество чего-либо. Чего именно? А все равно! Множества придумали математики, а им безразлично, что считать. Так подать сюда математика, и пусть ответит за всех! Скоро явился математик, взял два кружочка – черный и белый – и, протерев свои толстые очки, стал объяснять. Вот суть его речи.

Рис. 80 – Множества точек черного (B) и белого (W) кругов
Вы полагаете, что это кружочки? Нет, друзья, это два множества точек, – одно принадлежит черному кругу, другое – белому. Обозначим первое из них латинской буквой B (от Black – «черный»), а второе буквой W (от White – «белый»). Итак, черные и белые точки этих кружков назовём элементами множеств. Сколько там этих точек? Доказано, что бесконечно много, но к свойствам множеств это не имеет отношения. Что же это за свойства?
Добавление к множеству существующих элементов
Покройте черный круг таким же или меньшим черным кругом, или почеркайте его углем, – заметите разницу? Если на белый круг наложить такой же, или почеркать его мелом, – тоже не увидите изменений. Значит, множество не изменится при добавлении к нему элементов, уже входящих в это множество. На языке математики это свойство выразится так:
B + B = B
или так:
W + W + W = W
Не правда ли, странная арифметика?
Объединение множеств
Продолжим наши мысленные опыты и перекрасим оба круга в серый цвет. Будем считать их теперь одной фигурой, разорванной на части.

Рис. 81 – Объединение непересекающихся множеств G = B + W
Так мы получили новое множество, представляющее сумму или объединение двух предыдущих. Обозначим это новое множество буквой G (от Gray – «серый») и выразим то, что сделали, формулой.
G = B + W
Очевидно, что число точек во вновь образованном множестве равно их сумме в двух исходных. Пока в этом нет ничего интересного, – ведь исходные множества B и W, как говорят математики, не пересекаются. Сблизим круги так, чтобы добиться их частичного перекрытия (рис. 82).

Рис.82 – Объединение пересекающихся множеств G < B + W
Теперь количество точек в объединенном множестве будет меньше, чем в двух исходных по отдельности.
G < B + W
В общем случае при объединении множеств (как пересекающихся, так и не пересекающихся) соблюдается правило.
G ? B + W
Пересечение множеств
Иногда математиков (и не только их) интересует область пересечения множеств, отметим её серым цветом (рис. 83).
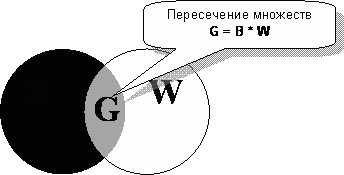
Рис.83 – Пересечение множеств G = B * W
Операцию пересечения множеств обозначают знаком умножения.
G = B • W
Количество точек в пересечении, как понимаете, не может быть больше, чем в любом из исходных множеств B и W. Для этого случая справедливо утверждение: пересечение множеств не больше любого из них.
B • W ? B и B • W ? W
Вычитание множеств
О солнечных и лунных затмениях слышали все, а кто-то и наблюдал их. Для математика это зримые примеры вычитания множеств; взгляните на рис. 84 – чем не затмения? Серую область можно трактовать как результат вычитания одного круга из другого. На левом рисунке белый круг «отгрыз» часть черного, превратив его в серую область, а на правом – наоборот. Подобающие этим случаям формулы будут таковы.
G = B – W или G = W – B

Рис.84 – Вычитание множеств
А если вычитаемый круг окажется больше того, из которого вычитают, и полностью поглотит его? В алгебре разность получится отрицательной, а здесь? Ничего подобного! При вычитании большего множества из меньшего или равного ему получается пустое множество, оно обозначается символом ?. Из пустого множества тоже можно вычитать, и результатом опять будет пустое множество.
(B – B) – B = ?
(? – W) – B = ?
Вот такими интересными свойствами обладают множества!
Подмножества и надмножества
На рис. 85 белый круг полностью поглощен черным. Тогда говорят, что множество точек белого круга составляет подмножество точек черного. Или так: множество точек черного круга является надмножеством точек белого. Математик выразит это формулой:
B > W

Рис.85 Надмножество (B) и подмножество (W)
А если круги совпадают и полностью перекрывают друг друга? Тогда говорят, что множества равны, и любое из них является и подмножеством, и надмножеством другого. В общем случае:
если B ? W, то B является надмножеством W;
если B ? W, то B является подмножеством W.
Числовые множества
Мы рассмотрели несметные множества бесконечно маленьких точек. Но компьютеры ещё не умеют работать с бесконечностями. Так умерим свой аппетит и перейдем к множествам с конечным числом элементов. Поступим так: вместо раскраски кругов расставим на них ряд жирных точек и пронумеруем их числами от 1 до 9 (рис. 86). В ходе последующих опытов нас будут интересовать лишь эти избранные точки (то есть, числа).
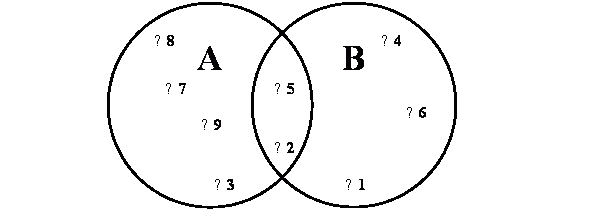
Рис.86 – Множества чисел
Так мы получили два конечных множества чисел. Одно из них, обозначенное буквой A, содержит числа 8, 7, 9, 3, 5, 2. Другое обозначено буквой B и включает числа 5, 4, 6, 1, 2. Эти множества математики записали бы так:
A = { 8, 7, 9, 3, 5, 2 }
B = { 5, 4, 6, 1, 2 }
Для записи множеств они используют фигурные скобки. Обратите внимание: числа в скобках следуют в произвольном порядке. Это значит, что порядок перечисления элементов множества не важен. Учтите также, что числа 2 и 5 входят в оба множества.
Подобно точкам на круге, каждый элемент числового множества уникален, иными словами, может входить в множество лишь единожды. Вспомните нашу попытку покрасить углем черный круг, – добавление к множеству существующих в нём элементов не изменяет его. Этим же свойством обладают и числовые множества. Например, для нашего случая справедливо следующее.
A + { 8, 7 } = A
Множество A после объединения с множеством {8,7} не изменилось, поскольку уже содержало эти числа.
С числовыми множествами поступают так же, как и с бесконечными: объединяют, пересекают, вычитают и сравнивают. Вот примеры этих операций для нашего случая.
Объединение множеств содержит все числа исходных множеств, при этом повторения (дубликаты) отбрасывают:
G = A + B = { 8, 7, 9, 3, 5, 2 } + { 5, 4, 6, 1, 2 } = { 8, 7, 9, 3, 5, 2, 4, 6, 1 }
Хотя числа 2 и 5 входили в оба исходных множества, в объединении они встречаются по разу.
Пересечение множеств содержит только числа, входящие в оба множества:
A * B = { 8, 7, 9, 3, 5, 2 } * { 5, 4, 6, 1, 2 } = { 5, 2 }
Разность множеств A–B содержит числа, состоящие в множестве A, но отсутствующие в множестве B:
A – B = { 8, 7, 9, 3, 5, 2 } – { 5, 4, 6, 1, 2 } = { 8, 7, 9, 3 }
Разность множеств B–A содержит числа, состоящие в множестве B, но отсутствующие в множестве A:
B – A = { 5, 4, 6, 1, 2 } – { 8, 7, 9, 3, 5, 2 } = { 4, 6, 1 }
Эти «вычисления» легко проверить по рис. 86.
Мощность множества, полные и неполные множества
Мощность множества – это наибольшее количество элементов, которое может содержаться в нём. В нашем числовом примере мощность множества равна девяти.
Множество, содержащее все возможные свои элементы, называют полным. В нашем случае полным является объединение множеств A+B.
Множество, содержащее не все возможные элементы, является неполным. Так, множества A и B по отдельности – неполные.
Все это рассказал нам математик. А что же Семен Семенович, или мы забыли о директоре? Нет, конечно, но к директорской задаче мы вернемся после ознакомления с «паскалевскими» множествами.
Итоги
• Множество – это совокупность различимых объектов (точек, чисел, предметов), которую мы воспринимаем как нечто целое. Отдельные объекты множества называют его элементами.
• К множествам применим ряд операций: объединение, пересечение, вычитание, сравнение.
• Объединение двух множеств содержит по одному элементу из каждого исходного множества.
• Пересечение двух множеств содержит только общие их элементы. Если таких элементов нет, пересечение будет пустым.
• Разность множеств содержит элементы уменьшаемого множества за исключением элементов вычитаемого множества.
• Первое множество является подмножеством второго, если все элементы первого принадлежат второму. И тогда второе множество будет надмножеством первого. Множества совпадают, если содержат одни и те же элементы.
А слабо?
А) Полицейская база данных некоторого государства содержит номера всех автомобилей, сгруппированные в ряд множеств. Три множества составлены по типам автомобилей: легковые, грузовые, автобусы. Шесть множеств образованы по цвету автомобилей: множества белых, черных, желтых, красных, синих и зеленых.
• Пересекается ли множество легковых автомобилей с множеством грузовых? А множество желтых автомобилей с множеством черных?
• Может ли быть непустым пересечение множества желтых автомобилей с множеством автобусов?
• Свидетель дорожно-транспортного происшествия сообщил, что с места преступления скрылся грузовой автомобиль синего цвета. Как вычислить группу подозреваемых автомобилей?
• На улице висит знак: грузовым проезд запрещен. Как определить множество автомобилей, въезд которым разрешен?
Б) Два государства, назовем их A и B, спорят о некой территории, – каждое считает ее своей. Нарисуйте на листочке предполагаемую карту, заштрихуйте спорную область, а затем объясните:
• Как вычислить спорную область государств?
• Как вычислить бесспорную область, включая оба государства?
• Заштрихуйте область, отвечающую формуле G = (A-B) + (B-A).
• Заштрихуйте область, отвечающую формуле G = A+B – A•B. Совпадает ли она с той, что вычислена по предыдущей формуле?
В) Дайте ответы на следующие вопросы.
• Является ли множество ваших одноклассников подмножеством учеников вашей школы?
• Пересекается ли множество ваших друзей с множеством ваших одноклассников?
• Является ли множество ваших друзей подмножеством ваших одноклассников?
- Только для взрослых
- Детям до 16–ти
- Глава 1 Путь далек у нас с тобою…
- Глава 2 Вместо теории
- Глава 3 Консольный интерфейс
- Глава 4 Оружие – к бою!
- Глава 5 Программа номер один
- Глава 6 Подготовка к следующему штурму
- Глава 7 Развиваем успех
- Глава 8 Постоянные и переменные
- Глава 9 Переменные: продолжение знакомства
- Глава 10 Условный оператор
- Глава 11 Операторный блок
- Глава 12 Цикл с проверкой в конце
- Глава 13 Правда и кривда
- Глава 14 Дважды два – четыре
- Глава 15 Айда в Монте-Карло!
- Глава 16 Делу время, а потехе час
- Глава 17 И вновь за парту
- Глава 18 Аз, Буки
- Глава 19 Процедуры и функции: разделяй и властвуй
- Глава 20 Процедуры: первый опыт
- Глава 21 Отладка
- Глава 22 О передаче параметров
- Глава 23 Функции
- Глава 24 Криптография
- Глава 25 Текстовые файлы
- Глава 26 Я не читатель, – я писатель!
- Глава 27 Дайте кораблю минутный отдых!
- Глава 28 Редактор и справочная система
- Глава 29 Читайте по-новому
- Глава 30 Журнальная история
- Глава 31 Финал журнальной истории
- Глава 32 Порядковые типы данных
- Глава 33 Вещественные числа
- Глава 34 Структура программы
- Глава 35 Множества
- Глава 36 Множества в Паскале
- Глава 37 Ввод и вывод множеств
- Глава 38 Множества в «бою»
- Глава 39 Командная игра (массивы)
- Глава 40 Пристрелка на знакомых мишенях
- Глава 41 По порядку, становись!
- Глава 42 Кто ищет, тот всегда найдет
- Глава 43 Сортировка по-взрослому
- Глава 44 Строки
- Глава 45 Очереди и стеки
- Глава 46 Огромные числа
- Глава 47 Системы счисления
- Глава 48 Железная логика
- Глава 49 Сложные массивы
- Глава 50 Неспортивные рекорды (записи)
- Глава 51 Указатели в море памяти
- Глава 52 Динамические переменные
- Глава 53 Массив указателей
- Глава 54 Односвязные списки
- Глава 55 Слова, слова, слова…
- Глава 56 И снова очереди, и снова стеки…
- Глава 57 Графомания
- Глава 58 По графу шагом марш!
- Глава 59 Крупные проекты
- Глава 60 Мелкие хитрости
- Глава 61 «Кубики» программиста (ООП)
- Глава 62 Самое интересное только начинается!
- Приложение А Установка и настройка IDE Borland Pascal
- Приложение Б Консольная программа в среде Delphi
- Приложение В Особенности IDE Pascal ABCNet
- Приложение Г Зарезервированные слова
- Приложение Д Ошибки компиляции
- Приложение Е Ошибки исполнения
- Приложение Ж Директивы управления компиляцией
- Приложение З Назначение пунктов меню
- Приложение И Стандартная кодировка символов MS–DOS
- Приложение К Некоторые встроенные процедуры и функции
- Приложение Л Перечень программ
- Приложение М Пример олимпиадной задачи
- Библиография
- Содержание книги
- Популярные страницы
- Операции с множествами узлов
- 8.1.22. Чередование массивов
- 2. Реляционные базы данных
- 3. Схемы отношений. Именованные значения кортежей
- 4. Полнота системы правил Армстронга
- Размытые функции
- 9.7.4. Иерархии классов и абстрактные классы
- Листинг 9.3. Пример JavaScript-файла, закрывающего всплывающее окно
- Глава 12 Краткий курс JavaScript
- 9.7.1. Определение подкласса
- IBPP для разработки C++
- Пример 1




