Книга: Песни о Паскале
Глава 38 Множества в «бою»
Разделы на этой странице:
Глава 38
Множества в «бою»
Множества, множества… – заполучив столь острое оружие, удержимся ли не пустить его в ход? Вот ещё несколько задач, – мы изрубим их в капусту!
Активисты, шаг вперед!
Прежде всего, отдадим долги Семену Семеновичу. Мы обещали директору выявить разгильдяев, что отлынивают от кружков, и сдержали слово. Теперь найдем активистов, состоящих в нескольких кружках. Откуда подступиться к этой задаче?
Положим для простоты, что в школе лишь три кружка, их списки представлены множествами S1, S2 и S3. Выявить тех, кто состоит одновременно в кружках S1 и S2 легко, – достаточно найти пересечение S1*S2. Точно так же поступим с другими парами: S1 и S3, S2 и S3. Объединив все три пересечения, мы выявим интересующих нас школяров. Итак, решение задачи выразится формулой.
R := S1*S2 + S1*S3 + S2*S3;
Попадут ли в это множество ученики, состоящие во всех трех кружках? Если да, то, как их отделить от прочих? Придумайте, как выявить тех, кто состоит:
• в трех кружках:
• в двух кружках и не более;
• только в одном из кружков.
Надеюсь, что с этим проектом, назовем его «P_38_1», вы справитесь сами, желаю успеха!
Подвиг контрразведчика
Контрразведка некоторого государства обнаружила утечку информации из лабораторий секретного учреждения. Для поимки шпиона позвали сыщика Шерлока Ивановича Холмского. Первым делом, он попросил списки сотрудников лабораторий. Лаборатории именовались латинскими буквами: «A», «B», «C» и так далее, причем некоторые сотрудники допускались в несколько лабораторий. Шерлок Иванович оцифровал списки, заменив фамилии сотрудников их табельными номерами, то есть, уникальными числами. Затем сгруппировал эти числа по лабораториям и составил табл. 6.
Табл. 6 – Исходные данные для «вычисления» завербованного сотрудника
| Лабо–ратория | Номера сотрудников, допущенных в лабораторию |
| A | 1 2 4 5 9 11 13 15 22 23 24 25 27 30 31 37 41 42 43 44 45 46 48 50 51 56 64 70 72 73 74 75 76 77 82 84 86 87 89 92 95 97 98 101 102 103 104 105 106 107 108 111 113 116 117 118 124 125 127 130 132 133 134 138 143 144 145 147 149 150 |
| B | 16 21 22 23 24 25 26 27 28 29 31 33 35 37 39 41 44 47 49 50 51 52 54 55 56 57 59 61 62 65 66 69 70 71 72 77 78 79 81 83 84 85 91 92 93 94 95 96 98 100 101 103 107 108 109 112 113 115 117 118 119 121 122 124 129 |
| C | 1 3 5 9 12 19 22 25 33 34 41 42 46 50 52 55 56 57 58 59 61 66 69 72 80 81 82 84 87 88 94 97 99 100 101 102 112 119 121 123 125 129 134 137 138 139 149 152 153 154 155 157 158 165 166 168 171 172 180 184 185 190 193 194 198 199 205 213 216 220 |
| D | 5 6 7 8 9 10 11 12 13 14 16 18 21 22 23 24 27 28 29 30 31 32 34 35 38 40 41 42 43 44 45 46 47 48 51 52 53 54 55 57 58 59 60 61 62 63 64 65 66 67 70 71 73 74 75 76 78 79 80 81 82 84 85 86 88 89 91 92 93 94 95 96 97 98 99 100 104 105 106 107 108 111 112 113 115 116 117 118 119 120 |
| E | 10 15 16 26 33 40 42 44 50 53 65 67 74 79 82 83 85 87 90 91 93 99 106 108 110 120 121 124 125 132 135 146 148 149 151 156 157 158 163 166 168 169 171 175 183 184 189 195 197 205 206 207 216 220 221 225 226 227 241 244 |
| F | 8 12 21 25 26 29 30 31 34 48 49 50 52 55 59 60 62 70 71 73 83 85 90 91 92 93 94 96 97 99 100 102 103 104 105 106 108 119 121 122 124 127 128 130 132 141 142 144 156 160 165 166 169 171 173 176 179 191 192 195 199 200 207 209 220 221 222 224 226 229 233 234 236 239 240 |
| G | 23 24 26 27 29 30 35 36 41 42 44 45 46 49 52 55 56 58 60 61 63 64 65 68 72 74 76 77 81 82 86 87 88 90 93 94 95 96 97 98 100 101 102 107 108 109 112 113 114 115 117 120 123 127 132 133 135 137 138 143 145 146 147 150 152 155 156 159 161 162 163 164 165 168 170 172 177 178 179 180 |
| H | 15 17 19 20 21 22 23 26 28 29 30 32 33 34 36 38 41 42 44 45 46 48 49 52 57 60 62 65 66 68 73 74 77 78 83 84 85 88 89 90 91 92 95 96 97 98 99 100 101 102 103 104 107 108 115 116 118 127 128 129 130 131 134 135 136 137 139 145 146 150 151 152 154 157 160 161 164 166 167 172 173 177 178 179 180 182 185 188 189 190 193 195 197 204 207 |
Дальнейшее разбирательство показало, что утечка секретов случалась только из лабораторий «A», «D», «G» и «H» (в таблице они выделены серым цветом). При этом секреты остальных лабораторий («B», «C», «E» и «F») остались нетронутыми. Это направило дедуктивную мысль в правильное русло.
«Очевидно, – рассуждал Шерлок Иванович, – шпионить может тот, кто допущен в «дырявые» лаборатории. Из этого круга исключим тех, кто работает в нетронутых лабораториях, иначе их секреты тоже стали бы известны». Рассудив так, Шерлок Иванович достал ноутбук, и через 30 минут агент был вычислен, – подозреваемым оказался сотрудник с номером 45. Установленная за ним слежка подтвердила подозрение, и шпион был задержан.
Слабо ли вам повторить подвиг контрразведчика? Воспроизведите программу, написанную Шерлоком Ивановичем, я подскажу вам только её первую строку.
{ P_38_2 – подвиг контрразведчика }
В тридевятом царстве
Это случилось на затерянном в океане материке, что носил на себе несколько царств-государств. Жители материка – те ещё скряги – тратили для названий своих стран всего по одной букве: «A», «B», «C» и так далее. И мы будем их так называть. Границами стран служили каналы, специально для того прорытые; каналы были пронумерованы. Некоторые страны выходили к океану, берега которого тоже были пронумерованы и служили границами.
Самым могущественным было царство «A». Однако, ввиду его обширности и частых политических перемен, тамошний государь никак не мог уяснить точные границы своей страны. Он толком не знал даже ближайших соседей, – сведения были самыми разноречивыми. Когда терпение монарха лопнуло, он повелел своим инженерам запустить спутник, который бы исследовал границы и внес ясность в этот вопрос.
Слово царя – закон, и вскоре спутник кружился на орбите. С высоты ясно наблюдались берега океана и каналы, составлявшие границы царств. Рис. 87 показывает то, что «увидел» спутник. Буквами обозначены названия стран, а числами – участки границ. В центре континента темным цветом выделено обширное царство «A». К нему примыкают несколько стран, отмеченные серым, – это его соседи. Страны, примыкающие к царству «A» уголками своих границ, соседями не считаются. Они и все прочие «не соседи» отмечены белым цветом, а вокруг – океан.
К сожалению, примитивная техника тех лет не смогла отправить на землю эту фотографию. Спутник передал лишь номера границ каждого государства в виде текстового файла, содержащего строчки чисел.
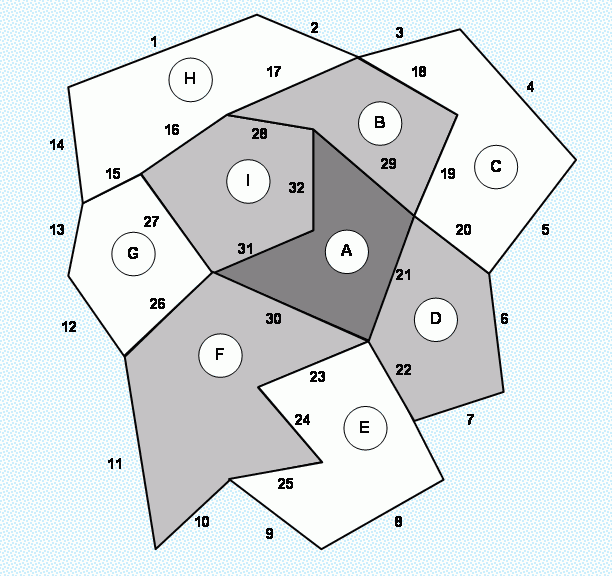
Рис.87 – Вид на материк из космоса
Выдернув из принтера ещё теплую распечатку файла, первый министр примчался во дворец, протянул листок монарху и покорно припал к подножию трона. Царь встрепенулся, стал разглядывать бумажку, вертеть её так и сяк, и даже на зуб попробовал. Наконец терпение государя иссякло: «Болван, – обратился он к министру, – покажи тут наших соседей. Что? Не можешь? Так проваливай с глаз долой!». И смятая распечатка угодила в лицо министра. «А ведь хотел, как лучше…» — стучало в башке убегающего премьера. «А получилось, как всегда!» — догнал его вопль взбешённого монарха.
Куда податься бедолаге? Разумеется, к самому умному, – к придворному программисту. «Выручай, браток, я тебе премию выпишу!». Инженеры, создавшие спутник, тоже не остались в стороне и растолковали программисту суть проблемы. Расправив скомканную царской рукой бумагу, Ник – так звали придворного программиста – увидел вот что.
29 21 30 31 32
17 18 19 29 28
3 4 5 20 19 18
6 7 22 21 20
8 9 25 24 23 22
10 11 26 30 23 24 25
12 13 15 27 26
14 1 2 17 16 15
16 28 32 31 27
Каждая строка этого файла, – объяснили инженеры, – перечисляет границы некоторого царства: первая строка – царства «A», вторая – царства «B» и так далее. Имена стран в файле не указаны, но подразумевается их алфавитный порядок. Надо составить список стран, которые соседствуют с нашей страной «A» – первой в этом списке.
Друзья, отложите книгу и попытайтесь решить эту интересную задачу. В случае успеха, я похлопочу за вас при дворе!
А пока вы раздумываете, я исполню свой долг перед историей и покажу решение заморского коллеги. Ник сразу понял, что имеет дело с двумя видами множеств: множеством границ, обозначенных числами, и множеством стран, обозначенных буквами (вы помните, что страны именовались буквами?). Парень смекнул, что две страны соседствуют тогда, когда пересечение множеств их границ не пусто (это значит, что у них есть общие границы). Дальше его мысли устремились так быстро, что пальцы едва успевали тыкать по клавишам. Вот плод его труда.
{ P_38_3 – поиск стран–соседей }
type TBoundSet = set of byte; { множество границ }
TStateSet = set of Char; { множество стран }
{––––– Распечатка множества стран (символов) –––––}
procedure WriteCharSet(var aFile: text; const aSet : TStateSet);
var c : char;
begin
for c:='A' to 'Z' do if c in aSet then Write(aFile, c:2);
Writeln(aFile);
end;
{––––– Ввод множества границ (чисел) –––––}
procedure ReadSet(var aFile: text; var aSet : TBoundSet);
var k : integer;
begin
While not Eoln(aFile) do begin
Read(aFile, K); aSet:= aSet+[K];
end;
Readln (aFile);
end;
var FileIn, FileOut: text;
R: TStateSet; { множество соседей (результат) }
SA, S : TBoundSet; { границы царства «A» и прочих }
State: char; { буква с названием очередной страны }
begin {––––– Главная программа –––––}
Assign(FileIn, 'P_38_3.in'); Reset(FileIn);
Assign(FileOut, ''); Rewrite(FileOut);
R:= []; SA:=[]; State:='A'; { начнем с царства «A» }
ReadSet(FileIn, SA); { из первой строки читаем границы для «A»}
while not Eof (FileIn) do begin { цикл по странам }
State:= Succ(State); { буква следующей страны }
S:=[]; ReadSet(FileIn, S); { читаем границы страны }
{ если граничит с царством «A», добавляем к результату }
if S*SA <> [] then R:= R + [State];
end;
WriteCharSet(FileOut, R); Readln; { вывод результата }
Close(FileIn); Close(FileOut);
end.
Программа Ника вычислила, что царство «A» соседствует с царствами «B», «D», «F», «I». Со временем проверка на местности это подтвердила.
Царь щедро наградил программиста, но история на этом не закончилась. О великом научном успехе скоро знала и последняя собака на материке. Но больше других этот успех заинтересовал купцов, плативших пошлины при пересечении границ. Они явились к Нику с предложением, от которого тот не смог отказаться. Хотите продолжения сказки? – оно ждёт вас в главах 49, 57 и 58.
Решето Эратосфена
Древние греки не знали, что они древние. И компьютеров тоже не знали, зато дышали бодрящим морским воздухом, коротая досуг в философских и математических размышлениях. Греческий досуг оказался не таким уж пустым, – иные задачки, придуманные под ласковый шепот волн, не решены по сию пору! Одна из них – вычисление простых чисел.
Прежде всего, выясним, что это за числа? Простым называют число, которое делится без остатка лишь на само себя и единицу. Все прочие числа являются составными. Возьмем, к примеру, числа от 1 до 10 и выделим среди них составные.
1 2 3 4 5 6 7 8 9 10
Здесь отмечены составные числа 4, 6, 8, 9 и 10, – они делятся без остатка либо на 2, либо на 3. Оставшиеся числа 1, 2, 3, 5 и 7 являются простыми.
Кто-то из греков задался вопросом: можно ли вычислить очередное простое число, если известны все предыдущие? Например, исходя из того, что числа 1, 2, 3 и 5 простые, определить следующее простое число (7). Как ни мудрили мудрецы, такой формулы или алгоритма пока не придумали! Но усилия в этом направлении породили целые отрасли математики, – вот такой полезный неуспех!
Размышлял над задачей и грек Эратосфен. Он тоже не решил её, однако нашел остроумный способ отсеивать простые числа, не превышающие некоторого числа N. Вот суть его идеи.
Положим, мы ищем простые числа не превышающие 20. Выпишем на морском песочке в ряд числа с 1 до 20. Первые два числа – 1 и 2 – простые, их не тронем, а среди остальных сотрем каждое второе, то есть 4, 6, 8 и так далее.
Затем находим первое нестертое число – это три. Сотрем каждое третье после тройки: 6, 9, 12, 15 и 18 (хотя часть из них уже стерта, лишний раз это сделать не повредит). Повторяя процедуру, находим следующее нестертое число – это пять. Стираем каждое пятое после пятерки: 10, 15, 20 (хотя все они уже стерты). Достигнув середины этого списка – числа 11, остановимся. Дальше двигаться нет смысла, поскольку на песке остались лишь простые числа.
Примечание. Если говорить точнее, лучше остановиться на числе, которое составляет корень квадратный из числа N, в данном случае это 5. Но для упрощения задачи мы будем обрабатывать больше чисел – половину ряда.
Вот результат этой пляжной математики, где стираемые числа выделены, а стертые обозначены звездочками. Здесь хватило всего двух просевов.
1-й отсев чисел, кратных 2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2-й отсев чисел, кратных 3:
1 2 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 *
Результат – простые числа:
1 2 3 * 5 * 7 * * * 11 * 13 * * * 17 * 19 *
А если бы Эратосфен жил в наше время? Стал бы он царапать на песке? Конечно, нет, – на что ж тогда компьютеры? Программа «P_38_4» находит все простые числа, не превышающие 255, – роль песка исполняет множество чисел.
program P_38_4; { Решето Эратосфена }
var Simples : set of byte; { множество чисел }
n, m : integer;
F : text;
begin
Assign(F, 'P_38_4.out'); Rewrite(F);
Simples:= [2..255]; { Сначала множество полное }
{ Цикл вычеркивания составных чисел }
for n:=2 to (255 div 2) do begin
{ если число ещё не вычеркнуто }
if n in Simples then
{ проверяем на кратность ему все последующие }
for m:=2*n to 255 do
{ если остаток(m/n) равен нулю, то m – составное }
if (m mod n)=0
{ и его надо вычеркнуть из множества}
then Simples:= Simples – [m];
end;
{ Распечатка множества простых чисел }
for n:=2 to 255 do if n in Simples then Writeln(F,n);
Close(F); Readln;
end.
Мелочь, а приятно
Одну из первых своих программ мы снабдили разумом попугая, научив повторять имя пользователя. После ввода имени в переменную S программа печатала.
Writeln (’Здравствуй, ’+ S);
Сделаем её чуть умнее, научив отличать мальчиков от девочек. По крайней мере, для русских имен. Русские женские имена оканчиваются на буквы «а» или «я» (Анна, Светлана, Мария и так далее), чего не скажешь о мужских. Последнюю букву имени можно «выдернуть» в символьную переменную C таким оператором.
C:= S[Length(S)];
И теперь приветствовать пользователя можно так:
if (C=’А’) or (C=’а’) or (C=’Я’) or (C=’я’)
then Writeln (’Здравствуй, девочка ’+ S)
else Writeln (’Здравствуй, мальчик ’+ S);
Здесь проверяется совпадение переменной C с буквами верхнего и нижнего регистров, поскольку нельзя предсказать, в каком регистре будет введено имя. Условный оператор выглядит громоздко, но, призвав на помощь множество, мы упростим его.
if C in [’А’, ’а’, ’Я’, ’я’]
then Writeln (’Здравствуй, девочка ’+ S)
else Writeln (’Здравствуй, мальчик ’+ S);
Переменную C проверяем на попадание в множество символов. Согласитесь, этот вариант читается приятней.
Итоги
Если вовремя смекнуть, что имеете дело с множествами, сложные задачи, как по волшебству, превратятся в простые!
А слабо?
А) Напишите программу для решения директорских задач и повторите подвиг контрразведчика. Или слабо?
Б) На острове действовали забавные законы по части транспортных средств – автобусов, грузовиков и легковушек. Во-первых, общее количество автомобилей на острове не должно было превышать 256. Автомобилям назначались номера с 0 до 255, при этом соблюдались следующие правила.
Номера, делившиеся без остатка на 7, назначались автобусам. Те, что делились без остатка на 5, назначались грузовикам, а все прочие – легковушкам. Например, номера 35 и 70 (они делятся и на 7, и на 5) доставались автобусам, а не грузовикам.
Схожие правила применялись и к окраске автомобилей, а именно: если номер авто делился на 4, его красили красным, если на 3 – желтым, если на 2 – белым, а остальные автомобили красили черным.
• Сформируйте три множества по классам автомобилей – автобусы, грузовики и легковушки. Вычислите количество машин каждого класса (Ответ: 37, 44, 175).
• Сформируйте четыре множества по цвету автомобилей – красные, желтые, белые и черные. Определите количество машин каждого цвета (Ответ: 64, 64, 43, 85).
• Столица того государства – деревня Кокосовка – страдала от пробок. Для их устранения ввели ограничение на въезд транспорта. Так, в один из дней недели в столицу пускали только красные легковушки, белые грузовики и все автобусы. Найдите номера всех этих машин. Сколько всего автомобилей могло въехать в столицу в тот день?
В) Полицейская база островного государства содержала номера угнанных автомобилей – числа от 1 до 255. Это был текстовый файл такого, например, вида:
120 31 16 25
То есть, номера перечислялись через пробел и следовали в произвольном порядке, что неудобно при поиске вручную. Ваша программа должна создать файл с номерами, упорядоченными по возрастанию. Подсказка: примените множество чисел.
Г) Генерация пароля длиной не менее восьми символов. В пароль входят символы трёх сортов: цифры, маленькие и большие латинские буквы, например: «7UpJ7rsT», «PasCal701». Сделайте четыре варианта так, чтобы соблюдались следующие условия:
• символ каждого сорта входит в пароль не менее двух раз, некоторые символы могут повторяться;
• все символы пароля уникальны (примените множество);
• символы одного сорта не соседствуют, например: «Pa7sCaL5», уникальность символов не требуется;
• символы одного сорта не соседствуют и все символы уникальны.
Д) Напишите четыре булевы функции, проверяющие, является ли введенная пользователем строка правильно сформированным паролем согласно условиям предыдущей задачи.
- Только для взрослых
- Детям до 16–ти
- Глава 1 Путь далек у нас с тобою…
- Глава 2 Вместо теории
- Глава 3 Консольный интерфейс
- Глава 4 Оружие – к бою!
- Глава 5 Программа номер один
- Глава 6 Подготовка к следующему штурму
- Глава 7 Развиваем успех
- Глава 8 Постоянные и переменные
- Глава 9 Переменные: продолжение знакомства
- Глава 10 Условный оператор
- Глава 11 Операторный блок
- Глава 12 Цикл с проверкой в конце
- Глава 13 Правда и кривда
- Глава 14 Дважды два – четыре
- Глава 15 Айда в Монте-Карло!
- Глава 16 Делу время, а потехе час
- Глава 17 И вновь за парту
- Глава 18 Аз, Буки
- Глава 19 Процедуры и функции: разделяй и властвуй
- Глава 20 Процедуры: первый опыт
- Глава 21 Отладка
- Глава 22 О передаче параметров
- Глава 23 Функции
- Глава 24 Криптография
- Глава 25 Текстовые файлы
- Глава 26 Я не читатель, – я писатель!
- Глава 27 Дайте кораблю минутный отдых!
- Глава 28 Редактор и справочная система
- Глава 29 Читайте по-новому
- Глава 30 Журнальная история
- Глава 31 Финал журнальной истории
- Глава 32 Порядковые типы данных
- Глава 33 Вещественные числа
- Глава 34 Структура программы
- Глава 35 Множества
- Глава 36 Множества в Паскале
- Глава 37 Ввод и вывод множеств
- Глава 38 Множества в «бою»
- Глава 39 Командная игра (массивы)
- Глава 40 Пристрелка на знакомых мишенях
- Глава 41 По порядку, становись!
- Глава 42 Кто ищет, тот всегда найдет
- Глава 43 Сортировка по-взрослому
- Глава 44 Строки
- Глава 45 Очереди и стеки
- Глава 46 Огромные числа
- Глава 47 Системы счисления
- Глава 48 Железная логика
- Глава 49 Сложные массивы
- Глава 50 Неспортивные рекорды (записи)
- Глава 51 Указатели в море памяти
- Глава 52 Динамические переменные
- Глава 53 Массив указателей
- Глава 54 Односвязные списки
- Глава 55 Слова, слова, слова…
- Глава 56 И снова очереди, и снова стеки…
- Глава 57 Графомания
- Глава 58 По графу шагом марш!
- Глава 59 Крупные проекты
- Глава 60 Мелкие хитрости
- Глава 61 «Кубики» программиста (ООП)
- Глава 62 Самое интересное только начинается!
- Приложение А Установка и настройка IDE Borland Pascal
- Приложение Б Консольная программа в среде Delphi
- Приложение В Особенности IDE Pascal ABCNet
- Приложение Г Зарезервированные слова
- Приложение Д Ошибки компиляции
- Приложение Е Ошибки исполнения
- Приложение Ж Директивы управления компиляцией
- Приложение З Назначение пунктов меню
- Приложение И Стандартная кодировка символов MS–DOS
- Приложение К Некоторые встроенные процедуры и функции
- Приложение Л Перечень программ
- Приложение М Пример олимпиадной задачи
- Библиография
- Содержание книги
- Популярные страницы
- Глава 1 Путь далек у нас с тобою…
- 42. «Разделение доходов» Обоюдный выигрыш через симбиоз
- Песни о Паскале
- Операции с множествами узлов
- Использование возможностей множества транзакций
- Множества объектов kset
- Этап 6 - выделение множества дизъюнктов
- 9.1. Множества
- 9.1.1. Простые операции над множествами
- 9.6.1. Пример: класс множества
- Получение множества наборов результатов с помощью объектов чтения данных
- 2.1.3. Подмножества модели и сохраняемые отображения




