Книга: Песни о Паскале
Глава 42 Кто ищет, тот всегда найдет
Разделы на этой странице:
- Где эта улица, где этот дом?
- Последовательный поиск
- Двоичный поиск
- Рис.90 – Поимка зайца шестью сетями
- Рис.91 – Двоичный поиск в отсортированном массиве
- Исследование двоичного поиска
- Рис.92 – Блок-схема алгоритма двоичного поиска
- Ах, время, время!
- Логарифмы? Это просто!
- Рис.93 – Сравнение времени линейного и двоичного поискаИтоги
- А слабо?
Глава 42
Кто ищет, тот всегда найдет

Все кругом ищут что-то: Карабас-Барабас – золотой ключик, Лиса с Котом – дураков, а Буратино – Страну Дураков. И я ищу: то ключи в карманах, то тапочки под диваном. А сколько всего таится в Интернете! Благо, искать информацию там помогают компьютеры.
Где эта улица, где этот дом?
В 40-й главе мы смастерили программу для поиска угнанных автомобилей. Испытаем её вон на той легковушке. Вводим номер машины и… оп! Вот так удача! Автомобильчик-то в розыске, – надо вернуть его владельцу. Однако, кто он? Где живет? А телефончик не подскажете? К сожалению, в нашей базе данных этих сведений нет, – её следует дополнить.
Добавим в программу поиска автомобилей массив строк, где будем хранить сведения о владельце: его имя, фамилию и телефон.
const CNumbers = 100; { размер массивов }
type TNumbers = array[1..CNumbers] of integer;
TNames = array[1..CNumbers] of string;
var Numbers : TNumbers; { массив номеров автомобилей }
Names : TNames; { массив сведений о владельце }
Здесь добавлен массив Names (имена), содержащий столько же строк, сколько номеров в базе данных. Эти строки соответствуют элементам массива номеров Numbers. Так, если элемент Numbers[7] содержит число 123, а элемент Names[7] – строку «Горбунков С.С., тел. 11-22-33», то значит, гражданин Горбунков владеет автомобилем с номером 123.
Что связывает массивы Names и Numbers? Ответ очевиден – общий индекс. Определив индекс автомобиля в массиве номеров, мы получим доступ и к сведениям о его владельце в строковом массиве.
Последовательный поиск
Напомню, что в полицейской базе данных из 40-й главы заголовок функции поиска был таким.
function FindNumber(aNum: integer): boolean;
Функция FindNumber выясняет, существует ли искомый номер в массиве Numbers, то есть она дает булев результат. Теперь этого мало, – хочется получить индекс элемента, где хранится искомый номер. А если такого номера в массиве нет? Пусть тогда функция вернет некоторое условное значение, например, минус единицу.
С учетом этих пожеланий, напишем новую функцию поиска и дадим ей имя FindSeq (от слов Find – «искать», Sequence – «последовательно»).
{ Функция поиска в массиве Numbers позиции числа aNum }
function FindSeq (aNum: integer): integer;
var i: integer;
begin
FindSeq:= -1; { если не найдем, то результат будет -1 }
for i:=1 to Fact do
if aNum=Numbers[i] then begin
FindSeq:= i; { нашли, возвращаем индекс }
Break; { выход из цикла }
end
end;
Новая функция сравнивает искомое число с элементами массива, перебирая их последовательно до тех пор, пока не найдет подходящий элемент или не уткнется в конец массива. В случае успеха она вернет индекс элемента в массиве, а иначе – минус единицу.
Этот способ называют поиском прямым перебором или линейным поиском. Линейный поиск прост, но крайне медлителен. Если бы библиотекарь искал заказанную книгу прямым перебором, клиент дремал бы в ожидании заказа месяцами! Но библиотекарь справляется с поиском, живо находя нужное среди сотен тысяч томов. Как ему удается это?
Все дело в порядке. Там, где порядок, искать проще и быстрей. Вы ищите ложку в кухонном шкафу, а ботинки – на обувной полке, но не обшариваете весь дом. Есть свой порядок и в библиотеке, потому персонал и справляется с работой. Компьютер ищет куда быстрее человека, и все же понуждать его к линейному поиску – проявление крайней жестокости. Впрочем, пострадает не столько компьютер, сколько уснувший в томлении пользователь.
Двоичный поиск
Один удачливый зверолов в минуту откровенности поделился секретом своих успехов. «Вначале я делю лес своей огромной сетью примерно пополам, и выясняю, в которой из двух половин очутился нужный мне зверь – пояснил охотник. – Затем половину со зверем опять делю пополам и гляжу, где он теперь. И так поступаю, пока животное не окажется в тесном загоне». И зверолов нацарапал на песке рис. 90.
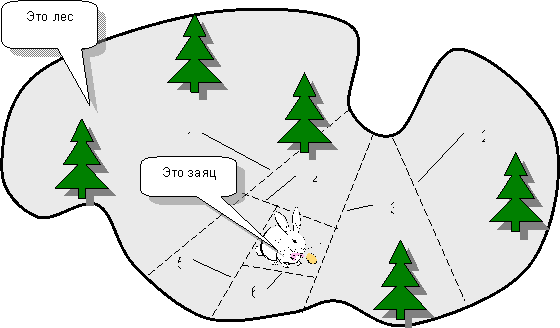
Рис.90 – Поимка зайца шестью сетями
Здесь показано, как шестью сетями (они обозначены цифрами) был изловлен несчастный заяц. Обратите внимание на нумерацию сетей, – они расставлялись в этом порядке.
Не воспользоваться ли уловкой зверолова для поиска в массиве? Ускорит ли это дело? Конечно! Но массив должен быть заранее отсортирован. На рис. 91 показан отсортированный по возрастанию массив, содержащий 12 чисел. Для наглядности числа изображены столбиками. Среди них я выбрал наугад число 32, и прямым перебором нашел его позицию (индекс) в массиве. Очевидно, что я выполнил 8 шагов поиска, поскольку число 32 хранится в 8-м элементе массива.
А теперь применим метод зверолова. Обратимся к среднему элементу массива, индекс которого равен полу-сумме первого и последнего индексов, то есть:
(1+12)/2 = 6
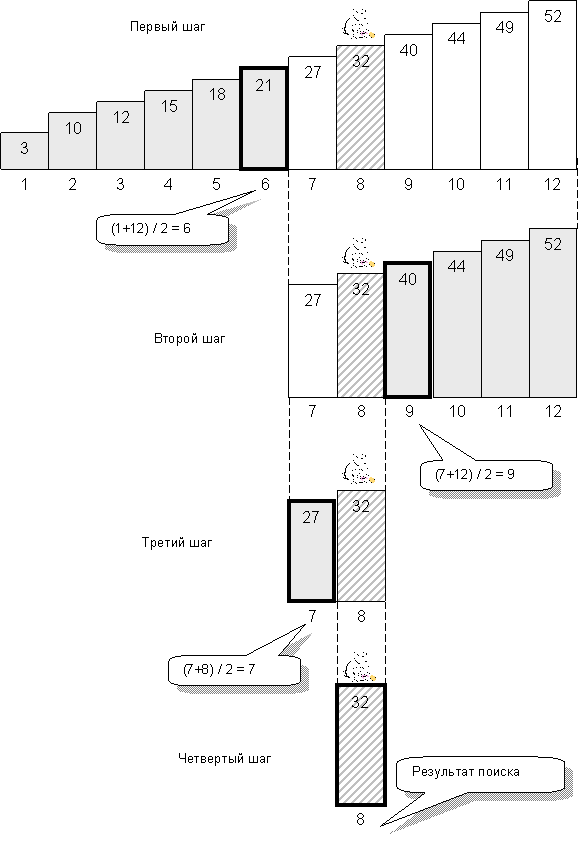
Рис.91 – Двоичный поиск в отсортированном массиве
Поскольку индекс – это целое число, дробную часть при делении отбросим. Итак, в позиции 6 оказалось число 21, которое меньше искомого числа 32. Это значит, что «зверь притаился» где-то правее. Раз так, элементы массива, расположенные левее, нас уже не интересуют, – мысленно отбросим их.
С оставшейся частью массива поступим точно так же, то есть, исследуем средний его элемент с индексом
(7+12)/2 = 9
Сравним «живущее» там число 40 с искомым числом 32. На этот раз оно оказалось больше искомого, а значит, искать надо левее, а все, что справа, отбросить. Так, на третьем шаге поиска из 12 элементов массива остались лишь два. Рассуждая тем же порядком, выделяем элемент с индексом
(7+8)/2 = 7
и отбрасываем на этот раз число 27. И вот на последнем четвертом шаге остался лишь один элемент с искомым числом 32.
Подведем итог: вместо 8 шагов последовательного поиска, метод зверолова сделал то же самое за 4 шага. Скажете: всего-то? Восемь шагов или четыре – разница невелика. Так проверим оба метода на большом наборе данных, – поищем в массиве из тысячи чисел. Только избавьте меня от ручной работы, – этот эксперимент поручим компьютеру, для чего соорудим несложную программу.
Исследование двоичного поиска
Частью этой программы будет функция двоичного поиска, алгоритм которой раскрыл зверолов. Но не худо привести и блок-схему этого чудесного изобретения. На блок-схеме (рис. 92), как и в программе, индексы элементов обозначены начальными буквами соответствующих английских слов: L – левый индекс (Left), R – правый индекс (Right), и M – средний индекс (Middle).
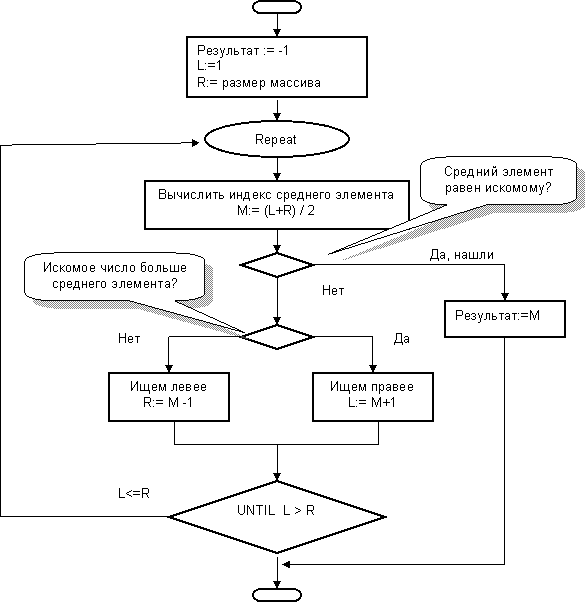
Рис.92 – Блок-схема алгоритма двоичного поиска
Функцию, работающую по этому алгоритму, я назвал FindBin (Find – «поиск», Binary – «двоичный»), она показана ниже. Полагаю, что приведенных в ней комментариев будет достаточно.
{ Функция двоичного поиска }
function FindBin (aNum: integer): integer;
var L, M, R : integer; { левый, правый и средний индексы }
begin
FindBin:= -1; { результат на случай неудачи }
L:= 1; R:= CSize; { начальные значения индексов }
repeat
M:= (L+R) div 2; { индекс среднего элемента }
if aNum= ArrSort[M] then begin
FindBin:= M; { нашли ! }
Break; { успешный выход из цикла }
end;
if aNum > ArrSort[M] { где искать дальше? }
then L:= M+1 { ищем правее }
else R:= M–1; { ищем левее }
until L > R; { выход при неудачном поиске }
end;
Теперь мы готовы создать исследовательскую программу, которая будет сравнивать два способа поиска.
Поступим так. Объявим два массива по 1000 чисел в каждом. Заполним их случайным образом и один из них отсортируем. Затем сделаем ряд экспериментов, каждый из которых состоит в следующем. Выбрав наугад одно из чисел массива, программа вызовет по очереди две функции: сначала последовательно найдет число в несортированном массиве, а затем двоичным поиском – в сортированном. Поскольку искомое число выбрано из массива, то поиск всегда будет успешным. Затраченные на поиск шаги подсчитаем, и результаты запишем в текстовый файл. После каждого такого эксперимента программа будет ожидать команды пользователя: приняв число ноль, она завершится, а иначе повторит эксперимент.
Подсчет шагов будем вести в глобальной переменной Steps (шаги). Перед вызовом функций поиска она обнуляется, а внутри функций наращивается (эти операторы внутри функций выделены курсивом). Вот и все, полюбуйтесь на эту «экспериментальную установку», введите в компьютер и запустите на выполнение.
{ P_42_1 – Исследование методов поиска }
const CSize = 1000; { размер массива }
{ объявление типа для массива }
Type TNumbers = array [1..CSize] of integer;
Var ArrRand : TNumbers; { несортированный массив }
ArrSort : TNumbers; { сортированный массив }
Steps : integer; { для подсчета числа шагов поиска }
{ Процедура "пузырьковой" сортировки чисел в порядке возрастания }
procedure BubbleSort(var arg: TNumbers);
var i, j, t: Integer;
begin
for i:= 1 to CSize-1 do { внешний цикл }
for j:= 1 to CSize-i do { внутренний цикл }
if arg[j] > arg[j+1] then begin { обмен местами }
t:= arg[j]; arg[j]:= arg[j+1]; arg[j+1]:= t;
end;
end;
{ Функция последовательного поиска (Find Sequence) }
function FindSeq (aNum: integer): integer;
var i: integer;
begin
FindSeq:= -1; { если не найдем, результат будет -1 }
for i:=1 to CSize do begin
Steps:= Steps+1; { подсчет шагов поиска }
if aNum= ArrRand[i] then begin
FindSeq:= i; { нашли, возвращаем позицию }
Break; { выход из цикла }
end;
end;
end;
{ Функция двоичного поиска (Find Binary) }
function FindBin (aNum: integer): integer;
var L, M, R : integer;
begin
FindBin:= -1;
L:= 1; R:= CSize;
repeat
Steps:= Steps+1; { подсчет шагов поиска }
M:= (L+R) div 2;
if aNum= ArrSort[M] then begin
FindBin:= M; { нашли ! }
Break; { выход из цикла }
end;
if aNum > ArrSort[M]
then L:= M+1
else R:= M-1;
until L > R;
end;
{--- Главная программа ---}
Var i, n, p : integer; { вспомогательные переменные }
F: text; { файл результатов }
begin
Assign(F,'P_42_1.OUT'); Rewrite(F);
{ Заполняем массив случайными числами }
for i:=1 to CSize do ArrRand[i]:=1+Random(10000);
ArrSort:= ArrRand; { копируем один массив в другой }
BubbleSort(ArrSort); { сортируем второй массив }
repeat { цикл с экспериментами }
i:= 1+ Random(CSize); { индекс в пределах массива }
n:= ArrRand[i]; { случайное число из массива }
Writeln(F,'Искомое число= ', n);
Steps:=0; { обнуляем счетчик шагов поиска }
p:= FindSeq(n); { последовательный поиск }
Writeln(F,'Последовательный: ', 'Позиция= ',
p:3, ' Шагов= ', Steps);
Steps:=0; { обнуляем счетчик шагов поиска }
p:= FindBin(n); { двоичный поиск }
Writeln(F,'Двоичный поиск: ', 'Позиция= ',
p:3, ' Шагов= ', Steps);
Write('Введите 0 для выхода из цикла '); Readln(n);
until n=0;
Close(F);
end.
Вот результаты трех экспериментов.
Искомое число= 5026
Последовательный: Позиция= 544 Шагов= 544
Двоичный поиск: Позиция= 518 Шагов= 10
Искомое число= 8528
Последовательный: Позиция= 828 Шагов= 828
Двоичный поиск: Позиция= 854 Шагов= 10
Искомое число= 7397
Последовательный: Позиция= 100 Шагов= 100
Двоичный поиск: Позиция= 748 Шагов= 9
Я не поленился проделать 20 опытов, результаты которых занес в табл. 7. Среднее число шагов поиска для каждого из методов посчитано мною на калькуляторе и внесено в последнюю строку таблицы.
Табл. 7- Результаты исследования алгоритмов поиска
| Экспе-римент | Искомое число | Количество шагов поиска | |
| Последовательный поиск | Двоичный поиск | ||
| 1 | 5026 | 544 | 10 |
| 2 | 8528 | 828 | 10 |
| 3 | 7397 | 100 | 9 |
| 4 | 2061 | 52 | 9 |
| 5 | 8227 | 634 | 9 |
| 6 | 9043 | 177 | 10 |
| 7 | 4257 | 10 | 10 |
| 8 | 3397 | 704 | 5 |
| 9 | 4021 | 887 | 10 |
| 10 | 8715 | 815 | 9 |
| 11 | 6811 | 53 | 9 |
| 12 | 5959 | 141 | 10 |
| 13 | 928 | 859 | 7 |
| 14 | 3295 | 26 | 10 |
| 15 | 9534 | 935 | 10 |
| 16 | 1618 | 8 | 6 |
| 17 | 1066 | 105 | 8 |
| 18 | 7081 | 989 | 10 |
| 19 | 218 | 290 | 9 |
| 20 | 6927 | 952 | 10 |
| Среднее количество шагов | 455 | 9 | |
Что вы скажете об этом? Двоичный поиск дал превосходный результат, – любое число находится не более чем за 10 шагов! Это любопытно, и побуждает разобраться в алгоритме глубже.
Ах, время, время!
Принимаясь за что-либо, мы прикидываем, сколько времени займет то или иное дело. Поиск может отнять уйму времени, вот почему важно оценить его трудоемкость. Сравним алгоритмы поиска по затратам времени. Только время будем измерять не секундами, а особыми единицами – шагами поиска. Почему? Да потому, что у нас с вами разные компьютеры. Поскольку ваш «станок» мощнее, ту же работу он выполнит быстрее моего, а это нечестно! Мы ведь алгоритмы сравниваем, а не процессоры.
Если улыбнется удача, поиск завершится на первом шаге. Иногда – по закону подлости – тратится максимальное число шагов. Но эти крайние случаи – редкость; обычно поиск занимает какое-то промежуточное время, и наш эксперимент подтвердил это. Программистов интересует время поиска в двух случаях: в худшем, и в среднем (то есть, усредненное по многим случаям).
Начнем с линейного поиска. Очевидно, что в массиве из N элементов худшее время поиска составит N шагов. Что касается среднего времени, то чутье подсказывает, что оно составит половину максимального времени, то есть N/2. Судите сами: искомое число с равной вероятностью может оказаться и ближе и дальше середины массива. Табл. 7 подтверждает эту догадку, – среднее количество шагов там составило 455, что очень близко к значению 1000/2.
Теперь рассмотрим двоичный поиск. Вначале оценим худшее время. Рассудим так. Сколько шагов поиска нужно в массиве из одного элемента? Правильно, один. А теперь вспомним, что при двоичном поиске всякий раз отбрасывается половина оставшегося массива. Значит, посчитав, сколько раз число N делится пополам для получения единицы, мы определим максимальное число шагов. Так и поступим; следите, честно ли я «распилил» нашу тысячу.
1. 1000 / 2 = 500
2. 500 / 2 = 250
3. 250 / 2 = 125
4. 125 / 2 = 62
5. 62 / 2 = 31
6. 31 / 2 = 15
7. 15 / 2 = 7
8. 7 / 2 = 3
9. 3 / 2 = 1
При делении я отбрасывал дробную часть, поскольку в двоичном алгоритме так и делается. Всего потребовалось 9 операций деления. Это значит, что максимальное число шагов поиска равно 10 (с учетом поиска в одном оставшемся элементе). Удивительная прозорливость, – ведь наш эксперимент (табл. 7) показал то же самое!
Теперь оценим среднее время двоичного поиска. Думаете, что оно составит 10/2 = 5 шагов? Как бы ни так! Дело в том, что любой алгоритм поиска в среднем исследует половину массива. Двоичный поиск отбрасывает половину массива на первом же шаге. А это значит, что в среднем число шагов будет всего лишь на единицу меньше худшего, то есть 9. Смотрим в табл. 7, – точно! Наша догадка подтвердилась! Таким образом, двоичный поиск не только быстрее линейного, но и более предсказуем: его худшее время почти не отличается от среднего.
Логарифмы? Это просто!
Разобравшись с тысячей элементов, оценим трудоемкость двоичного поиска при других размерах массива. Метод оценки остается тем же: делим размер массива пополам до получения единицы.
Для таких вычислений математики придумали особую функцию – логарифм (не путайте её с рифмой, ритмом и алгоритмом!). Логарифмы бывают разные: десятичные, натуральные и прочие. Нам интересен двоичный логарифм, который по-научному называется так: «логарифм числа N по основанию два». Математики записывают его следующим образом:
Log2 N
Связь между числом N и его двоичным логарифмом легко проследить на следующих примерах. Слева представлено разложение на множители нескольких чисел, а справа – двоичные логарифмы этих же чисел.
4 = 2 • 2 Log2 4 = 2
16 = 2 • 2 • 2 • 2 Log2 16 = 4
64 = 2 • 2 • 2 • 2 • 2 • 2 Log2 64 = 6
Итак, двоичный логарифм числа равен количеству двоек (ой, нехорошее слово!), перемножаемых для получения этого числа. Например, для получения числа 8 надо перемножить три двойки, и его логарифм равен трем. Кстати, для получения единицы из восьмерки, её тоже «пилят» пополам трижды. Значит, оба способа вычисления логарифма – через умножение, и через деление – равноценны.
Если вы завтра же не забросите программирование, то табл. 8 с логарифмами нескольких чисел ещё пригодится вам.
Табл. 8 – двоичные логарифмы некоторых чисел
| N | Log2 N | N | Log2 N | N | Log2 N | N | Log2 N |
| 2 | 1 | 32 | 5 | 512 | 9 | 8192 | 13 |
| 4 | 2 | 64 | 6 | 1024 | 10 | 16384 | 14 |
| 8 | 3 | 128 | 7 | 2048 | 11 | 32768 | 15 |
| 16 | 4 | 256 | 8 | 4096 | 12 | 65536 | 16 |
По таблице можно оценить как среднее, так и худшее время двоичного поиска: среднее время равно двоичному логарифму от размера массива, а худшее – на единицу больше.
А как определить логарифмы других чисел, например, числа 50? Поскольку оно лежит между 32 и 64, его логарифм должен быть где-то между 5 и 6? Так оно и есть: логарифм 50 равен приблизительно 5,64 (это я на калькуляторе посчитал). Но, поскольку мы применяем логарифмы для подсчета шагов поиска, то погрешностью в доли шага можно пренебречь. К чему мелочиться? Будем считать, что логарифм числа 50 тоже равен 6. Мало того, назначим это значение логарифма всем числам в промежутке от 33 до 64.
На рис. 93 сопоставлен рост числа с ростом его логарифма. Когда число увеличивается вдвое, его логарифм возрастает лишь на единицу. Вот почему с ростом размера массива время двоичного поиска растет так медленно (что очень радует нас!).

Рис.93 – Сравнение времени линейного и двоичного поиска
Итоги
• Компьютерные базы данных (БД) содержат разнородную информацию, отдельные элементы которой связаны общим индексом.
• Поиск в массиве состоит в определении индекса искомого элемента; зная индекс, можно извлечь всю прочую информацию о нужном объекте.
• Для поиска применяют два способа: последовательный перебор и двоичный поиск.
• Последовательный перебор (линейный поиск) очень прост, но время поиска пропорционально размеру массива, что для больших объёмов данных бывает неприемлемо.
• Двоичный поиск очень быстр, – с ростом размера массива затраты времени на поиск растут по логарифмическому закону. Однако, двоичный поиск работает только в отсортированных массивах.
А слабо?
А). Будет ли линейный поиск работать быстрее в сортированном массиве? Проверьте на практике.
Б) Сколько шагов двоичного поиска потребуется в массиве из миллиона элементов? А из миллиарда? Сравните с трудоемкостью линейного поиска.
В) Напишите полицейскую базу данных, содержащую номера автомобилей и сведения о владельцах. Данные должны вводиться из файла, каждая строка которого содержит номер автомобиля и сведения о владельце, например:
123 Горбунков С.С., ул. Тепличная, д. 21, тел. 11-22-33
35 Стелькин И.Н., ул. Тенистая, д. 5, тел. 33-22-11
Примените массивы и учтите опыт обработки классного журнала.
Г) Отсортируйте полицейскую базу данных и напишите программу для двоичного поиска в ней.
Д) Папа Карло опасался Буратино, и прятал спички в сейфе. Код замка из четырех цифр он доверил лишь своему приятелю – честному малому Джузеппе, который не поддавался ни на какие уговоры деревянного мальчишки. Тогда тот пустился на хитрость. Ладно, – предложил Буратино, – не можешь открыть мне код, – не надо. Давай тогда в игру сыграем: я буду спрашивать, а ты отвечай только «да» или «нет». Первый вопрос был таким: код замка больше 5000? Через несколько минут Буратино уже рылся в папином сейфе. Сделайте программу для быстрого угадывания числа методом Буратино. Роль Буратино (угадывающего) должен исполнять компьютер.
- Только для взрослых
- Детям до 16–ти
- Глава 1 Путь далек у нас с тобою…
- Глава 2 Вместо теории
- Глава 3 Консольный интерфейс
- Глава 4 Оружие – к бою!
- Глава 5 Программа номер один
- Глава 6 Подготовка к следующему штурму
- Глава 7 Развиваем успех
- Глава 8 Постоянные и переменные
- Глава 9 Переменные: продолжение знакомства
- Глава 10 Условный оператор
- Глава 11 Операторный блок
- Глава 12 Цикл с проверкой в конце
- Глава 13 Правда и кривда
- Глава 14 Дважды два – четыре
- Глава 15 Айда в Монте-Карло!
- Глава 16 Делу время, а потехе час
- Глава 17 И вновь за парту
- Глава 18 Аз, Буки
- Глава 19 Процедуры и функции: разделяй и властвуй
- Глава 20 Процедуры: первый опыт
- Глава 21 Отладка
- Глава 22 О передаче параметров
- Глава 23 Функции
- Глава 24 Криптография
- Глава 25 Текстовые файлы
- Глава 26 Я не читатель, – я писатель!
- Глава 27 Дайте кораблю минутный отдых!
- Глава 28 Редактор и справочная система
- Глава 29 Читайте по-новому
- Глава 30 Журнальная история
- Глава 31 Финал журнальной истории
- Глава 32 Порядковые типы данных
- Глава 33 Вещественные числа
- Глава 34 Структура программы
- Глава 35 Множества
- Глава 36 Множества в Паскале
- Глава 37 Ввод и вывод множеств
- Глава 38 Множества в «бою»
- Глава 39 Командная игра (массивы)
- Глава 40 Пристрелка на знакомых мишенях
- Глава 41 По порядку, становись!
- Глава 42 Кто ищет, тот всегда найдет
- Глава 43 Сортировка по-взрослому
- Глава 44 Строки
- Глава 45 Очереди и стеки
- Глава 46 Огромные числа
- Глава 47 Системы счисления
- Глава 48 Железная логика
- Глава 49 Сложные массивы
- Глава 50 Неспортивные рекорды (записи)
- Глава 51 Указатели в море памяти
- Глава 52 Динамические переменные
- Глава 53 Массив указателей
- Глава 54 Односвязные списки
- Глава 55 Слова, слова, слова…
- Глава 56 И снова очереди, и снова стеки…
- Глава 57 Графомания
- Глава 58 По графу шагом марш!
- Глава 59 Крупные проекты
- Глава 60 Мелкие хитрости
- Глава 61 «Кубики» программиста (ООП)
- Глава 62 Самое интересное только начинается!
- Приложение А Установка и настройка IDE Borland Pascal
- Приложение Б Консольная программа в среде Delphi
- Приложение В Особенности IDE Pascal ABCNet
- Приложение Г Зарезервированные слова
- Приложение Д Ошибки компиляции
- Приложение Е Ошибки исполнения
- Приложение Ж Директивы управления компиляцией
- Приложение З Назначение пунктов меню
- Приложение И Стандартная кодировка символов MS–DOS
- Приложение К Некоторые встроенные процедуры и функции
- Приложение Л Перечень программ
- Приложение М Пример олимпиадной задачи
- Библиография
- Содержание книги
- Популярные страницы
- Профессиональная терминология не всегда уместна
- Пример 12-8. Частота встречаемости отдельных слов
- Домашняя мастерская: вы всегда на работе
- 9.1. Классы и прототипы
- Этот изменчивый мир
- Покупатель на крючке. Руководство по созданию продуктов, формирующих привычки
- Кто такой тест-менеджер
- Факторы выгоды
- Иерархия объектов в InterBase
- Кто сказал: «Яндекс»?
- Жизненные циклы продуктов
- Имена объектов длиной 68 символов




