Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Гильбертово пространство
Гильбертово пространство
Напомним, что в главе 5 для описания классической системы было введено понятие фазового пространства. Каждая точка фазового пространства используется для представления (классического) состояния физической системы как целого. В квантовой теории соответствующим аналогичным понятием является гильбертово пространство[147]. Одна точка гильбертова пространства представляет квантовое состояние системы как целого. Нам необходимо бросить хотя бы беглый взгляд на математическую структуру гильбертова пространства. Надеюсь, что читателя не устрашит такая перспектива. В том, что я намереваюсь сказать, нет ничего математически очень сложного, хотя некоторые идеи могут показаться непривычными.
Наиболее фундаментальное свойство гильбертова пространства заключается в том, что оно представляет собой так называемое векторное пространство, а фактически комплексное векторное пространство. Это означает, что, сложив любые два элемента гильбертова пространства, мы получим элемент, также принадлежащий этому же пространству. Кроме того, когда мы производим сложение элементов гильбертова пространства, их разрешается умножать на комплекснозначные веса. Мы должны уметь делать такие операции, ибо они входят в состав только что рассмотренной квантовой линейной суперпозиции, а именно операции, ранее давшие нам фотонные состояния ?t + ?b, ?t — ?b, ?t + i?b и т. д. По существу, все что мы имеем в виду, используя термин «комплексное векторное пространство», сводится к разрешению образовывать взвешенные суммы указанного типа[148].
Удобно принять систему обозначений (предложенную главным образом Дираком), согласно которой элементы гильбертова пространства называются векторами состояния и обозначаются угловыми скобками |?)[149] (важное примечание),
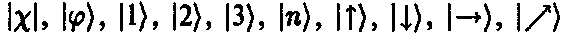
Теперь эти символы обозначают квантовые состояния. Операцию сложения двух векторов состояния мы записываем в виде
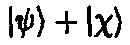
или с комплексными весами ? и z
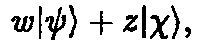
где ?|?) означает ? х |?) и т. д. Соответствующим образом мы можем записать приведенные выше комбинации ?t + ?b, ?t — ?b, ?t + i?b в виде
|?t) + |?b), |?t) — |?b), |?t) + i|?b), и т. д.
Мы можем также просто умножить одно состояние |?) на комплексное число ? и получить
?|?)
(в действительности это — частный случай приведенной выше комбинации состояний с комплексными весами при z = 0).
Напомним, что нам разрешается рассматривать комбинации с комплекснозначными весами ? и z и в том случае, когда ? и z — не являются амплитудами вероятности, а лишь им пропорциональны. Соответственно, мы принимаем правило, согласно которому весь вектор состояния можно умножить на отличное от нуля комплексное число, и физическое состояние от этого не изменится. (В результате такого умножения изменились бы значения весов ? и z, но отношение ?: z осталось бы неизменным.) Каждый из векторов
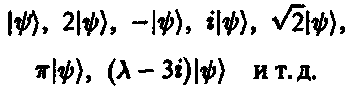
представляет одно и то же физическое состояние, как и любой вектор z |?), где z ? 0. Единственный элемент гильбертова пространства, не допускающий интерпретацию как физическое состояние, есть нулевой вектор 0 (начало координат гильбертова пространства).
Чтобы получить некоторое геометрическое представление этой картины, рассмотрим сначала более привычное понятие «вещественного» вектора. Такой вектор принято изображать просто как стрелку, проведенную на плоскости или в трехмерном пространстве. Сложение двух таких векторов производится по правилу параллелограмма (рис. 6.19).
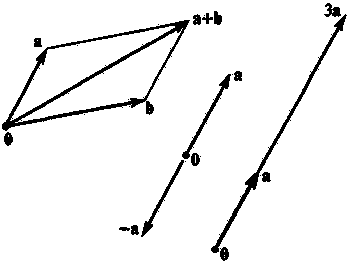
Рис. 6.19. Сложение и умножение на скаляры векторов в гильбертовом пространстве можно наглядно представить как соответствующие операции для векторов в обычном пространстве
Операция умножения вектора на положительное (вещественное) число сводится в таком представлении просто к умножению длины рассматриваемой стрелки на заданное число (направление стрелки при этом остается неизменным). Если же мы умножаем стрелку на отрицательное число, то направление стрелки изменяется на противоположное. Если число, на которое требуется умножить стрелку, равно 0, то мы получаем нулевой вектор 0, который не имеет направления. (Вектор 0 представлен «нулевой стрелкой», имеющей нулевую длину.) Одним из примеров векторной величины может служить сила, действующая на частицу. Другими примерами могут служить классические скорости, ускорения и импульсы. Существуют также 4-векторы импульса, которые мы рассматривали в конце предыдущей главы. Это — векторы не в двумерном и не в трехмерном пространстве, а в четырехмерном. Но для гильбертова пространства нам понадобятся векторы с гораздо большим числом измерений (в действительности, часто даже бесконечномерные, но для нас это обстоятельство сейчас несущественно). Напомним, что мы всегда использовали стрелки, чтобы изобразить векторы в классическом фазовом пространстве, которое могло иметь очень высокую размерность. Говоря об «измерениях» фазового пространства, как и об «измерениях» гильбертова пространства, мы не имеем в виду обычные пространственные направления. Отнюдь! Каждое измерение гильбертова пространства соответствует одному из различных независимых физических состояний квантовой системы.
Вследствие эквивалентности между |?) и z|?), физическое состояние в действительности соответствует целой прямой, проходящей через начало координат 0, (или лучу) в гильбертовом пространстве (описываемом всеми кратными некоторого вектора), а не просто каким-то конкретным вектором, лежащим на этой прямой. Луч состоит из всех возможных кратных некоторого конкретного вектора состояния |?). (Следует иметь в виду, что речь идет о комплексных кратных, поэтому прямая в действительности представляет собой комплексную прямую, но об этом пока лучше не беспокоиться!) (См. рис. 6.20.)
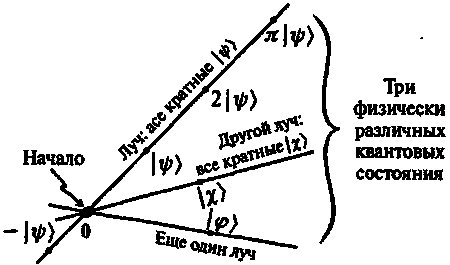
Рис. 6.20. Физические квантовые состояния описываются лучами в гильбертовом пространстве
Скоро пред нами предстанет весьма изящная картина такого пространства лучей для случая двумерного гильбертова пространства. Другой предельный случай — бесконечномерное гильбертово пространство. Бесконечномерное гильбертово пространство возникает даже в простой ситуации локализации одной частицы. Тогда для каждого возможного положения, которое могла бы занимать частица, существует целое измерение! Каждое положение частицы определяет в гильбертовом пространстве целую «координатную ось», поэтому с учетом бесконечно многих различных положений частицы мы имеем бесконечно много различных независимых направлений (или «измерений») в гильбертовом пространстве. Импульсные состояния также могут быть представлены в том же самом гильбертовом пространстве. Поскольку импульсные состояния представимы в виде комбинаций конфигурационных состояний, то они соответствуют осям, идущим «по диагонали» — наклоненным относительно осей в конфигурационном пространстве. Совокупность всех импульсных состояний дает нам новую систему осей, и переход от осей конфигурационного пространства состояний к осям импульсного пространства состояний сводится к повороту в гильбертовом пространстве.
Не следует пытаться наглядно представить себе это сколько-нибудь точно. Такая попытка была бы неразумной! Однако некоторые идеи, почерпнутые из обычной евклидовой геометрии, могут оказаться очень полезными. В частности, рассматриваемые нами оси (либо все оси в конфигурационном пространстве состояний, либо все оси в импульсном пространстве состояний) следует считать взаимно ортогональными, т. е. расположенными под «прямыми» углами друг к другу. «Ортогональность» лучей — понятие, важное для квантовой механики. Ортогональные лучи соответствуют состояниям, которые независимы друг от друга. Различные возможные конфигурационные состояния частицы все взаимноортогональны, как и все различные возможные импульсные состояния. Но конфигурационные состояния не ортогональны импульсным состояниям. Весьма схематично эта ситуация представлена на рис. 6.21.
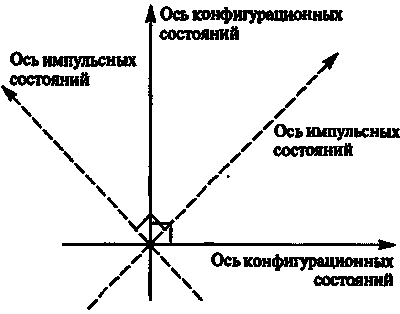
Рис. 6.21. Конфигурационные состояния и импульсные состояния приводят к различному выбору ортогональных осей в одном и том же гильбертовом пространстве
- Нужна ли философам квантовая теория?
- Проблемы с классической теорией
- Начало квантовой теории
- Эксперимент с двумя щелями
- Амплитуды вероятностей
- Квантовое состояние частицы
- Принцип неопределенности
- Эволюционные процедуры U и R
- Одна частица — сразу в двух местах?
- Гильбертово пространство
- Измерения
- Спин и сфера Римана состояний
- Объективность и измеримость квантовых состояний
- Копирование квантового состояния
- Спин фотона
- Объекты с большим спином
- Многочастичные системы
- «Парадокс» Эйнштейна, Подольского и Розена
- Эксперименты с фотонами: проблема для специальной теории относительности?
- Уравнение Шредингера; уравнение Дирака
- Квантовая теория поля
- Кошка Шредингера
- Различные точки зрения на существующую квантовую теорию
- К чему мы пришли после всего сказанного?
- 6.3 Пространство имен устройств
- Временное пространство сортировки
- Адресное пространство процесса
- 3.1. Адресное пространство Linux
- 20.3. Rinda: пространство кортежей в Ruby
- Глава 14 Адресное пространство процесса
- Пространство пользователя и параметр HZ
- Отображение файла на адресное пространство процесса
- Включение и отключение "использовать все пространство"
- 7 Контент-платформа: пространство, где контент живет и работает
- Глава 1 Пространство мифа
- Пространство или время




