Книга: Новый ум короля: О компьютерах, мышлении и законах физики

Многочастичные системы

Многочастичные системы

Квантовомеханические описания многочастичных состояний, к сожалению, очень сложны. В действительности такие описания чрезвычайно сложны. О них необходимо думать в терминах суперпозиций всех различных возможных расположений всех отдельных частиц! Это приводит к огромному числу возможных состояний — гораздо большему, чем в случае поля в классической теории. Мы уже видели, что квантовое состояние даже одной частицы, а именно волновая функция, обладает сложностями такого рода, которые характерны для всего классического поля. Эта картина (требующая для своего задания бесконечно большого числа параметров) гораздо сложнее, чем классическая картина одной частицы (для задания состояния которой требуется всего лишь небольшое число параметров — точнее, шесть параметров, если частица не обладает внутренними степенями свободы, например, спином; см. главу 5, «Гамильтонова механика»). Такая ситуация может показаться достаточно плохой, и можно было бы думать, что для описания квантового состояния двух частиц понадобится два поля, каждое из которых описывало бы состояние каждой частицы. Ничего подобного! Как мы увидим далее, в случае двух и более частиц описание квантового состояния становится гораздо сложнее.

Квантовое состояние одной (бесспиновой) частицы определяется комплексным числом (амплитудой) для каждого возможного положения, которое может занимать частица. Частица обладает амплитудой, чтобы находиться в точке А, и амплитудой, чтобы находиться в точке В, и амплитудой, чтобы находиться в точке С, и т. д. Подумаем теперь о двух частицах. Первая частица может находиться в точке А, а вторая, например, — в точке В. Возможность такого события должна была бы иметь некоторую амплитуду. С другой стороны, первая частица могла бы находиться в точке В, а вторая — в точке А, и такое расположение частиц также должно иметь некоторую амплитуду; возможно, что первая частица могла бы находиться в точке В, а вторая — в точке С или, может быть, обе частицы могли бы находиться в точке А. Каждый из этих возможных вариантов должен иметь некоторую амплитуду. Следовательно, волновая функция должна быть не просто парой функций положения (т. е. парой полей), а одной функцией двух положений!

Чтобы получить некоторое представление о том, насколько сложнее задать функцию двух положений по сравнению с двумя функциями положения, представим себе ситуацию, в которой существует лишь конечный набор допустимых положений. Предположим, что разрешены ровно 10 положений, заданных (ортонормированными) состояниями

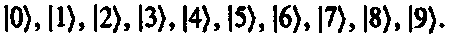
Тогда состояние |?) одной частицы было бы какой-то линейной комбинацией

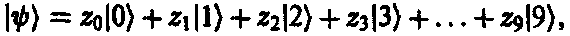
где различные коэффициенты z₀, z₁, z₂,…., z₉ дают, соответственно, амплитуды того, что частица находится попеременно в каждой из 10 точек. Десять комплексных чисел задают состояние одной частицы. В случае двухчастичного состояния нам понадобилось бы по одной амплитуде для каждой пары положений. Всего существуют

10² = 100

различных (упорядоченных) пар положений, поэтому нам потребовались бы 100 комплексных чисел! А если бы у нас были только два одночастичных состояния (т. е. «две функции положения», а не «одна функция двух положений», как в приведенном выше примере), то нам понадобилось бы всего лишь 20 комплексных чисел.

Пронумеруем эти 100 комплексных чисел следующим образом

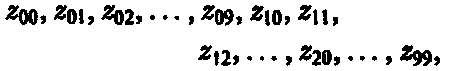
а соответствующие (ортонормированные) базисные векторы[162]

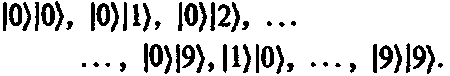
Тогда общее двухчастичное состояние можно было бы представить в виде

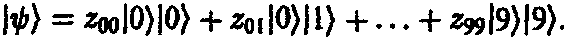
Такое обозначение состояний в виде «произведения» имеет следующий смысл: если |?) — возможное состояние первой частицы (не обязательно состояние с определенным положением) и если |?) — возможное состояние второй частицы, то состояние, в котором первая частица находится в состоянии |?), а вторая — в состоянии |?), можно представить в виде

|?) |?).

«Произведения» можно также брать между любыми другими парами квантовых состояний, а не обязательно между парами одночастичных состояний. Таким образом, мы всегда интерпретируем состояние-произведение |?) |?) (не обязательно состояний отдельных частиц) как конъюнкцию

«первая система находится в состоянии |?)» и

«вторая система находится в состоянии |?)»

(Аналогичная интерпретация справедлива и относительно |?) |?) |?) и т. д.; см. далее.) Однако общее двухчастичное состояние в действительности не имеет вид «произведения». Например, оно может быть представимо в виде

|?)|?) + |?)|?),

где |?) — еще одно возможное состояние первой системы,

а |?) — еще одно возможное состояние второй системы. Это состояние представляет собой линейную суперпозицию, а именно: суперпозицию первой конъюнкции состояний |?) и |?)плюс вторая конъюнкция состояний |?) и |?), и не может быть представлено в виде простого произведения (т. е. как конъюнкция двух состояний). Еще один пример — состояние |?)|?) — |?)|?) описывало бы другую такую линейную суперпозицию. Заметим, что квантовая механика требует проведения четкого различия между смыслом слов «плюс» и «и». И в обращении с этими словами нам следует быть более осторожными!

В случае трех частиц ситуация во многом аналогична. Чтобы задать общее трехчастичное состояние в приведенном выше примере, где имеются только 10 возможных положений, нам потребовалось бы теперь 1000 комплексных чисел! Полный базис для трехчастичных состояний состоял бы из следующих элементов:

|0)|0)|0), |0)|0)|1), |0)|0)|2), …, |9)|9)|9).

Частные трехчастичные состояния имели бы вид произведений трех сомножителей

|?)|?)|?)

(где |?), |?) и |?) — не обязательно состояния с определенным положением), но для общего трехчастичного состояния нам понадобилось бы построить суперпозицию большого числа состояний типа этих простых «произведений». Соответствующая схема получения общего состояния для четырех и более частиц должна быть очевидна.

До сих пор мы рассматривали случай различимых частиц, когда все частицы: «первая», «вторая», «третья» и т. д. принадлежат к разным типам. Одна из поразительных особенностей квантовой механики заключается в том, что в случае «тождественных» частиц правила коренным образом меняются. Действительно, правила становятся такими, что в самом прямом смысле частицы определенного типа должны быть не просто почти тождественными, а в точности тождественными. Это относится ко всем электронам и ко всем фотонам. Но оказывается, что все электроны тождественны друг другу совсем не так, как тождественны все фотоны! Различие заключается в том, что электроны принадлежат к так называемым фермионам, тогда как фотоны принадлежат к бозонам. Эти два класса частиц надлежит рассматривать весьма различным образом.

Прежде чем я окончательно запутаю читателя этими словесными несуразностями, позвольте мне попытаться объяснить, как действительно следует характеризовать фермионные и бозонные состояния. Правило состоит в следующем. Если |?) — состояние, содержащее некоторое число фермионов определенного типа, то при перестановке любых двух фермионов |?) должно перейти в — |?):

|?) ? — |?)

Если состояние |?) содержит некоторое число бозонов определенного типа, то при перестановке любых двух бозонов |?) должно перейти в |?):

|?) ? |?)

Отсюда следует, что никакие два фермиона не могут находиться в одном и том же состоянии. Действительно, если бы какие-нибудь два фермиона находились в одном и том же состоянии, то их перестановка вообще никак не сказывалась бы на полном состоянии системы, следовательно должно было бы выполняться — |?)=|?) т. е. |?)=0, что не допустимо для квантового состояния. Это свойство известно как принцип запрета Паули[163], а его следствия для структуры вещества имеют фундаментальный характер. Действительно, все главные составляющие вещества: электроны, протоны и нейтроны принадлежат к числу фермионов. Не будь принципа запрета, вещество бы просто сколлапсировало!

Вернемся к нашему примеру с 10 положениями и предположим теперь, что у нас есть состояние, состоящее из двух тождественных фермионов. Состояние |0)|0) исключается в силу принципа Паули (при перестановке первого множителя со вторым оно переходит в себя вместо того, чтобы переходить в себя со знаком минус). Кроме того, состояние |0)|1) также само по себе должно быть исключено, так как при перестановке множителей знак минус не появляется; но это легко можно исправить, если заменить произведение |0)|1) комбинацией

|0)|1) — |0)|1).

(Для нормировки оба члена можно было бы умножить на общий множитель 1/?2.) Это состояние правильно изменяет знак при перестановке первой частицы со второй, но теперь состояния |0)|1) и |0)|1) уже не независимы. Вместо этих двух состояний нам теперь разрешается иметь только одно состояние! Всего существует

1/2 (10 х 9) = 45

состояний такого рода — по одному на каждую неупорядоченную пару различных состояний из |0), |1)…., |9). Таким образом, для задания двухфермионного состояния в нашей системе необходимы 45 комплексных чисел. В случае трех фермионов нам требуются 3 различные позиции, и базисные состояния выглядят следующим образом

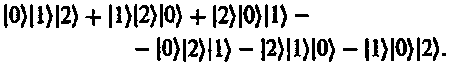
Всего таких состояний (10 х 9 х 8)/6 = 120, поэтому для задания трехфермионного состояния необходимы 120 комплексных чисел.

Для пары тождественных бозонов независимые базисные состояния бывают двоякого рода, а именно такие, как

|0)|1) + |1)|0),

и такие, как

|0)|0)

(которое теперь разрешается), что дает всего 10 х 11/2 = 55 базисных состояний. Таким образом, для задания двухбозонных состояний требуется 55 комплексных чисел. Для трех бозонов существуют базисные состояния трех различных типов и для задания каждого из них требуются (10 х 11 х 12)/6 = 220 комплексных чисел, и так далее.

Разумеется, для того, чтобы донести до читателя основные идеи, я рассматривал упрощенную ситуацию. Более реалистическое описание потребовало бы целый континуум состояний с определенным положением, но существенные идеи остаются такими же. Еще одно небольшое осложнение связано с наличием спина. Для каждой частицы со спином 1/2 (такая частица с необходимостью является фермионом) в каждом положении существовало бы 2 возможных состояния. Обозначим их «?» (спин «вверх») и «?» (спин «вниз»). Тогда в рассматриваемой нами упрощенной ситуации мы получаем не 10, а 20 базисных состояний

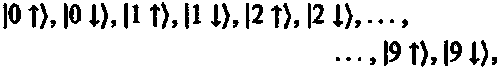
а в остальном рассуждать следует так же, как было сделано только что (таким образом, для двух таких фермионов необходимо взять (20 х 19)/2 = 190 чисел, для трех — (20 х 19 х 18)/6 = 1140 и т. д.).

В главе 1 я упоминал о том, что согласно современной теории, если частицу из тела человека поменять местами с аналогичной частицей из кирпича в стене его жилища, то ничего не произойдет. Если бы эта частица была бозоном, то, как мы знаем, состояние |?) действительно осталось бы совершенно не изменившимся. Если бы эта частица была фермионом, то состояние |?) в результате обмена частиц перешло бы в — |?) физически тождественное состоянию |?). (В случае необходимости изменение знака можно устранить с помощью простой меры предосторожности, а именно: при замене одной частицы на другую, повернуть одну из двух частиц на 360° вокруг ее оси. Напомним, что фермионы изменяют знак при таком повороте, а состояние бозонов остается неизменным!) Современная теория (существующая примерно с 1926 года) действительно сообщает нам нечто глубокое относительно индивидуального тождества мельчайших «кирпичиков» физической материи. Строго говоря, мы не можем говорить об «этом конкретном электроне» или об «индивидуальном фотоне». Утверждать, что «первый электрон находится здесь, а второй — там», означает утверждать, что состояние имеет вид |0)|1), что, как мы уже знаем, недопустимо, если речь идет о фермионном состоянии! Однако вполне допустимо утверждение о том, что «существует пара электронов, один из которых находится здесь, а другой — там». Вполне «законно» говорить о множестве всех электронов или всех протонов, или всех фотонов (хотя даже такое утверждение игнорирует взаимодействия между различными типами частиц). Индивидуальные электроны являются неким приближением такой полной картине, как, впрочем, и индивидуальные протоны или индивидуальные фотоны. Для большинства целей этого приближения вполне достаточно, но существуют различные ситуации, при которых оно не срабатывает — убедительными контрпримерами могут служить сверхпроводимость, сверхтекучесть и излучение лазера.

Картина физического мира, которую представила нам квантовая механика, — совсем не то, к чему мы привыкли в классической физике. Но придержите вашу шляпу — в квантовом мире есть гораздо более странные вещи!

Оглавление книги