Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Эксперимент с двумя щелями
Эксперимент с двумя щелями
Рассмотрим «архетипичный» квантовомеханический эксперимент, в котором пучок электронов, света или любых других «волн-частиц» направляется сквозь две узкие щели на расположенный позади них экран (рис. 6.3).
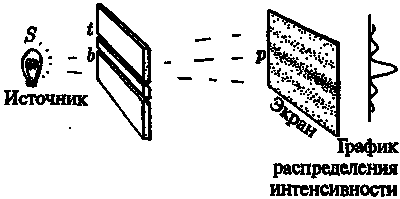
Рис. 6.З. Эксперимент с двумя щелями и монохроматическим светом (Обозначения на рисунке: S (англ. sourse) — источник, t (англ. top) — верхняя [щель], b (англ. bottom) — нижняя [щель]. — Прим. ред.)
Для большей конкретности выберем свет и условимся называть квант света «фотоном» согласно принятой терминологии. Наиболее очевидное проявление света как потока частиц (фотонов) наблюдается на экране. Свет достигает экрана в виде дискретных точечных порций энергии, которые всегда связаны с частотой света формулой Планка: Е = hv. Энергия никогда не передается в виде «половинки» (или иной доли) фотона. Регистрация фотонов представляет собой явление типа «все или ничего». Всегда наблюдается только целое число фотонов.
Но при прохождении через две щели фотоны обнаруживают волновое поведение. Предположим, что сначала открыта только одна щель (а вторая — наглухо закрыта). Пройдя через эту щель, пучок света «рассеивается» (это явление называется дифракцией и является характерным для распространения волн). Пока еще можно придерживаться корпускулярной точки зрения и считать, что расширение пучка обусловлено влиянием краев щели, заставляющем фотоны отклоняться на случайную величину в обе стороны. Когда свет, проходящий через щель, обладает достаточной интенсивностью (число фотонов велико), то освещенность экрана кажется равномерной. Но если интенсивность света уменьшить, то можно с уверенностью утверждать, что освещенность экрана распадется на отдельные пятна — в согласии с корпускулярной теорией. Яркие пятна располагаются там, где отдельные фотоны достигают экрана. Кажущееся равномерным распределение освещенности представляет собой статистический эффект, обусловленный очень большим числом участвующих в явлении фотонов (рис. 6.4).
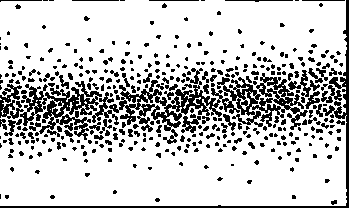
Рис. 6.4. Картина распределения интенсивности на экране, когда открыта только одна щель: наблюдается распределение дискретных крохотных пятнышек
(Для сравнения, 60-ваттная электрическая лампа излучает около 100 000 000 000 000 000 000 фотонов в секунду!) При прохождении через щель фотоны действительно отклоняются случайным образом. Причем отклонения на различные углы имеют различные вероятности, что и порождает наблюдаемое распределение освещенности на экране.
Но главная трудность для корпускулярной картины возникает, когда мы открываем вторую щель! Предположим, что свет излучается желтой натриевой лампой, это значит, что он имеет чистый цвет без примеси, или, если воспользоваться физическим термином, свет монохроматический, т. е. имеет одну определенную частоту, или, на языке корпускулярной картины, все фотоны имеют одну и ту же энергию. Длина волны в данном случае составляет около 5 х 10-7 м. Предположим, что щели имеют в ширину около 0,001 мм и отстоят друг от друга на расстояние около 0,15 мм, а экран находится от них на расстоянии около 1 м. При достаточно большой интенсивности света распределение освещенности все еще выглядит равномерным, но теперь в нем имеется некое подобие волнообразности, называемое интерференционной картиной — на экране примерно в 3 мм от центра наблюдаются полосы (рис. 6.5).

Рис. 6.5. Картина распределения интенсивности, когда открыты обе щели: наблюдается волнообразное распределение дискретных пятнышек
Открывая вторую щель, мы надеялись увидеть вдвое бо?льшую освещенность экрана (и это, действительно, было бы верно, если рассматривать полную освещенность экрана). Но оказалось, что теперь детальная картина освещенности полностью отлична от той, которая имела место при одной открытой щели. В тех точках экрана, где освещенность максимальна, его интенсивность оказывается не в два, а в четыре раза больше той, что была прежде. В других же точках, где освещенность минимальна, — интенсивность падает до нуля. Точки с нулевой интенсивностью, возможно, и представляют наибольшую загадку для корпускулярной точки зрения. Это те точки, которых фотон мог бы благополучно достичь, если бы открыта была только одна щель. Теперь же, когда мы открыли и вторую щель, неожиданно оказалось, что нечто помешало фотону попасть туда, куда он мог бы попасть прежде. Как могло случиться, что, предоставив фотону альтернативный маршрут, мы в действительности воспрепятствовали его прохождению по любому из маршрутов?
Если в качестве «размера» фотона принять длину его волны, то в масштабе фотона вторая щель находится от первой на расстоянии около 300 «размеров фотона» (а ширина каждой щели составляет около двух длин волн фотона) (рис. 6.6).
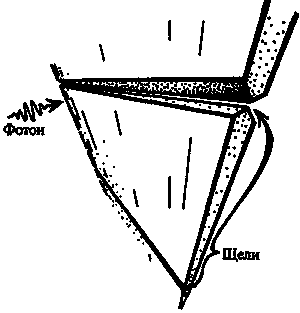
Рис. 6.6. Щели «с точки зрения» фотона! Разве может быть важно фотону, открыта или закрыта вторая щель, находящаяся на расстоянии около 300 «размеров фотона»?
Каким образом фотон, проходя через одну из щелей, «узнает» о том, открыта или закрыта другая щель? На самом деле, в принципе не существует предела для расстояния, на которое могут быть разнесены щели, для того, чтобы произошло явление «гашения или усиления».
Создается впечатление, что когда свет проходит через одну или две щели, он ведет себя как волна, а не как корпускула (частица)! Такое гашение — деструктивная интерференция — хорошо известное свойство обычных волн. Если каждый из двух маршрутов порознь может быть пройден волной, то когда для нее открыты оба маршрута, может оказаться, что они взаимно погасят друг друга. На рис. 6.7 показано, как это происходит.
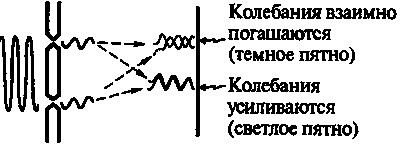
Рис. 6.7. Чисто волновая картина позволяет нам осмыслить распределение светлых и темных полос на экране (но не дискретность) на языке интерференции волн
Когда какая-то часть волны, пройдя через одну из щелей, встречает часть волны, прошедшую через другую щель, то они усиливают друг друга, если находятся «в фазе» (т. е. если встречаются два гребня или две впадины), или гасят друг друга, если они находятся «в противофазе» (т. е. гребень одной части встречается с впадиной другой). В эксперименте с двумя щелями яркие места на экране возникают там, где расстояния до щелей отличаются на целое число длин волн так, что гребни приходятся на гребни, а впадины — на впадины, а темные места возникают там, где разность этих расстояний равна полуцелому числу длин волн так, что гребни встречаются с впадинами, а впадины — с гребнями.
Нет ничего загадочного в поведении обычной макроскопической классической волны, проходящей одновременно через две щели. Волна в конечном счете представляет собой всего лишь «возмущение» либо некоторой непрерывной среды (поля), либо некоторого вещества, состоящего из мириад крохотных точечных частиц. Возмущение может частично пройти через одну щель, частично через другую щель. Но в корпускулярной картине ситуация иная: каждый отдельный фотон сам по себе ведет себя, как волна! В некотором смысле каждая частица проходит сразу через обе щели и интерферирует сама с собой! Ибо, если значительно уменьшить полную интенсивность света, то можно гарантировать, что вблизи щелей будет находиться не более одного фотона одновременно. Явление деструктивной интерференции, когда два альтернативных маршрута каким-то образом «ухитряются» исключить друг друга из числа реализованных возможностей, есть нечто, применимое к одному фотону. Если для фотона открыт только один из двух маршрутов, то фотон может пройти по нему. Если открыт другой маршрут, то фотон может пройти второй вместо первого маршрута. Но если перед фотоном открыты оба маршрута, то эти две возможности чудесным образом исключают друг друга, и оказывается, что фотон не может пройти ни по одному из маршрутов!
Настоятельно советую читателю остановиться и вдуматься в смысл этого необычного факта. Дело не в том, что свет ведет себя в одних случаях как волны, а в других как частицы. Каждая частица в отдельности сама по себе ведет себя, как волна; и различные альтернативные возможности, открывающиеся перед частицей, иногда могут полностью уничтожать друг друга!
Действительно ли фотон расщепляется на два и частично проходит через одну щель, а частично — через другую? Большинство физиков будут возражать против такой постановки вопроса. По их мнению оба маршрута, открытых перед частицей, должны вносить вклад в конечный результат, они — всего лишь дополнительные способы движения, и не следует думать, будто частица должна расщепиться на две, чтобы пройти через щели. В подтверждение той точки зрения, что частица не проходит частично через одну щель и частично — через другую, можно рассмотреть видоизмененную ситуацию, в которой около одной из щелей помещен детектор частиц. В этом случае фотон (или любая другая частица) всегда появляется как единое целое, а не как некоторая доля целого: ведь наш детектор регистрирует либо целый фотон, либо полное отсутствие фотонов. Однако, если детектор расположен достаточно близко к одной из щелей, чтобы наблюдатель мог различить, через какую из них прошел фотон, то интерференционная картина на экране исчезает. Для того, чтобы имела место интерференция, по-видимому, необходимо «отсутствие знания» относительно того, через какую из щелей «действительно» прошла частица.
Чтобы получить интерференцию, обе альтернативы должны дать свой вклад, иногда «суммируясь», усиливая друг друга в два раза больше, чем можно было бы ожидать, а иногда «вычитаясь», чтобы загадочным образом погасить друг друга. Фактически же согласно правилам квантовой механики в действительности происходит нечто еще более загадочное! Конечно, альтернативы могут суммироваться (самые яркие точки на экране), альтернативы могут вычитаться (темные точки), но они также могут образовывать и такие странные комбинации, как:
альтернатива А + i х альтернатива В,
где i — «квадратный корень из минус единицы» (i = ?-1), с которым мы уже встречались в главе 3 (в точках на экране с промежуточной интенсивностью освещенности). В сущности любое комплексное число может играть роль коэффициента в «комбинации альтернатив»!
Возможно, читатель уже вспомнил высказанное мной в главе 3 предупреждение о том, что комплексные числа играют «абсолютно фундаментальную роль в структуре квантовой механики». Комплексные числа — не просто математические диковинки. Физиков вынудили обратить на них внимание убедительные и неожиданные экспериментальные факты. Чтобы понять квантовую механику, мы должны поближе познакомиться с языком комплекснозначных весовых коэффициентов. Давайте же рассмотрим, к каким это приводит последствиям.
- Нужна ли философам квантовая теория?
- Проблемы с классической теорией
- Начало квантовой теории
- Эксперимент с двумя щелями
- Амплитуды вероятностей
- Квантовое состояние частицы
- Принцип неопределенности
- Эволюционные процедуры U и R
- Одна частица — сразу в двух местах?
- Гильбертово пространство
- Измерения
- Спин и сфера Римана состояний
- Объективность и измеримость квантовых состояний
- Копирование квантового состояния
- Спин фотона
- Объекты с большим спином
- Многочастичные системы
- «Парадокс» Эйнштейна, Подольского и Розена
- Эксперименты с фотонами: проблема для специальной теории относительности?
- Уравнение Шредингера; уравнение Дирака
- Квантовая теория поля
- Кошка Шредингера
- Различные точки зрения на существующую квантовую теорию
- К чему мы пришли после всего сказанного?
- Глава 6 Квантовая магия и квантовое таинство
- Как быстро переключаться между двумя пользователями, не закрывая их программ?
- В ходе экспериментов отключил Internet Explorer, теперь не могу его включить
- Как в документе Microsoft Word изменить расстояние между двумя словами?
- Основа для экспериментов
- Эксперименты с числовыми типами данных
- Выражения с двумя цифрами
- Экспериментаторские способности
- Глава 4 Эксперименты с диаграммами
- Система для шифрования с двумя ключами.
- Глава 7. Создание прототипов для экспериментов
- 7. Эксперимент. Как найти причины путем вмешательства в действия людей и систем




