Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Спин фотона
Спин фотона
Рассмотрим теперь «спин» фотона и его связь со сферой Римана. Фотоны действительно обладают спином, но поскольку они всегда движутся со скоростью света, их спин нельзя рассматривать как вращение вокруг какой-то неподвижной точки; ось спина фотона всегда совпадает с направлением движения. Спин фотона называется поляризацией. Поляризация — это явление, на котором основано действие «поляроидных» солнцезащитных очков. Возьмите два фрагмента поляроида, наложите их один на другой и посмотрите сквозь них. В общем случае вы увидите, что через них проходит некоторое количество света. Держа один из фрагментов неподвижно, поворачивайте другой фрагмент. Количество света, проходящего сквозь поляроиды, будет изменяться. При одной ориентации, когда проходит максимальное количество света, второй поляроид практически ничего не вычитает из светового потока, проходящего сквозь первый поляроид. Но при ориентации, выбранной под прямым углом к первой, свет практически вообще не проходит сквозь поляроиды.
Это явление легче всего понять в терминах волновой картины света. Здесь нам понадобится предложенный Максвеллом способ рассмотрения света как комбинации осциллирующих электрического и магнитного полей. На рис. 6.26 изображен плоскополяризованный свет. Электрическое поле осциллирует в плоскости, называемой плоскостью поляризации, а магнитное поле осциллирует в такт с электрическим, но в ортогональной плоскости.

Рис. 6.26. Плоскополяризованная электромагнитная волна
Каждый фрагмент поляроида пропускает свет, плоскость поляризации которого направлена вдоль структуры поляроида. Когда структура второго поляроида ориентирована так же, как структура первого, то весь свет, прошедший сквозь первый поляроид, проходит и сквозь второй. Но когда структуры двух поляроидов образуют прямой угол, то второй поляроид отсекает весь свет, прошедший сквозь первый поляроид. Если же два поляроида ориентированы друг относительно друга под некоторым углом ?, то второй поляроид пропускает долю, равную
cos2?,
света, прошедшего сквозь первый поляроид.
В корпускулярной картине мы должны считать, что каждый индивидуальный фотон обладает поляризацией. Первый поляроид действует как измеритель поляризации, давая ответ ДА, если фотон действительно поляризован в соответствующем направлении. В этом случае фотону разрешается пройти сквозь поляроид. Если же фотон поляризован в ортогональном направлении, то измерение первым поляроидом даст ответ НЕТ, и фотон будет поглощен. (В данном случае «ортогональность» в гильбертовом пространстве соответствует прямому углу между направлениями в обычном пространстве!) Предположим, что фотон проходит сквозь первый поляроид, после чего второй поляроид задает ему соответствующий вопрос, но уже относительно некоторого другого направления. Угол между этими двумя направлениями равен ?, как в упомянутом выше случае. Тогда мы имеем cos2? в качестве вероятности того, что фотон пройдет сквозь второй поляроид при условии, что он уже прошел сквозь первый поляроид.
Где же здесь появляется сфера Римана? Чтобы получить полный набор состояний поляризации, описываемый комплексными числами, нам необходимо рассмотреть круговую и эллиптическую поляризацию. Для классической волны эти разновидности поляризации представлены на рис. 6.27.
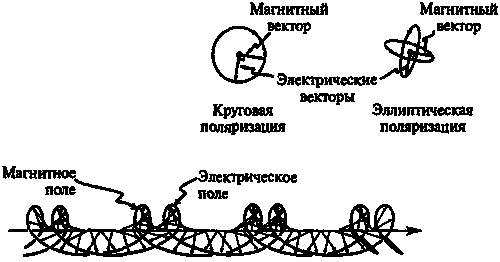
Рис. 6.27. Электромагнитная волна с круговой поляризацией. (Эллиптическая поляризация занимает промежуточное положение между плоской (рис. 6.26) и круговой (рис. 6.27) поляризацией.)
При круговой поляризации электрическое и магнитное поля не осциллируют, а согласованно вращаются, по-прежнему образуя между собой прямой угол. При эллиптической поляризации существует некоторая комбинация вращательного и колебательного движений, а вектор электрического поля «вычерчивает» в пространстве эллипс. В квантовом описании каждому индивидуальному фотону разрешается находиться в любом из спиновых состояний, т. е. быть поляризованным любым из названных выше способов.
Чтобы понять, как набор возможных поляризаций снова образует сферу Римана, представим себе фотон, который движется вертикально вверх. Северный полюс теперь представляет состояние |R) — правовинтовой спин. Это означает, что электрический вектор движущегося фотона вращается против часовой стрелки относительно вертикали (если смотреть сверху). Южный полюс представляет состояние |L) — левовинтовой спин. (Фотоны можно представлять вращающимися наподобие ружейной пули, либо слева направо, либо справа налево.) Общее спиновое состояние |R) + q|L) представляет собой комплексную линейную комбинацию двух состояний |R) и |L) и соответствует точке на сфере Римана, помеченной значением q. Чтобы установить связь между значением q и эллипсом поляризации, мы прежде всего извлечем из q квадратный корень и получим другое комплексное число р:
р = ?q
Затем нанесем р вместо q на сферу Римана и рассмотрим плоскость, проходящую через центр сферы перпендикулярно прямой, соединяющей центр сферы с точкой р. Эта плоскость пересекает сферу по окружности, проектируя которую на горизонталь, мы получаем эллипс поляризации (рис. 6.28)[160].
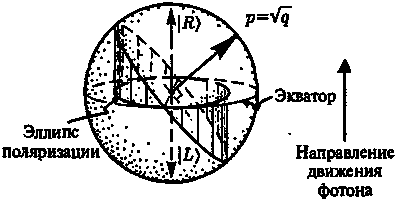
Рис. 6.28. Сфера Римана (но теперь со значениями ?q) также описывает состояния поляризации фотона. (Вектор, направленный в точку ?q, называется вектором Стока.)
Сфера Римана со значениями q по-прежнему описывает совокупность поляризованных состояний фотона, но квадратный корень р из q дает нам ее пространственную реализацию.
Чтобы вычислить вероятности, мы можем воспользоваться той же самой формулой 1/2(1 + cos v), которой мы пользовались для электрона, применив ее к q, а не к р. Рассмотрим плоскую поляризацию. Мы измеряем поляризацию фотона сначала в одном направлении, затем в другом направлении, образующем с первым угол ?. Эти два направления соответствуют двум значениям р на экваторе сферы, стягивающим угол ? в центре сферы. Так как величины р — квадратные корни из величин q, угол v, под которым из центра видны q-точки, вдвое больше угла, под которым из центра видны p-точки: v = 2?. Таким образом, вероятность получения ответа ДА после второго измерения при условии, что после первого измерения был получен ответ ДА (т. е. вероятность прохождения фотона через второй поляроид при условии, что он прошел сквозь первый поляроид) равна 1/2(1 + cos ?), что, как показывают несложные тригонометрические преобразования, в точности совпадает с cos2? и утверждалось выше.
- Нужна ли философам квантовая теория?
- Проблемы с классической теорией
- Начало квантовой теории
- Эксперимент с двумя щелями
- Амплитуды вероятностей
- Квантовое состояние частицы
- Принцип неопределенности
- Эволюционные процедуры U и R
- Одна частица — сразу в двух местах?
- Гильбертово пространство
- Измерения
- Спин и сфера Римана состояний
- Объективность и измеримость квантовых состояний
- Копирование квантового состояния
- Спин фотона
- Объекты с большим спином
- Многочастичные системы
- «Парадокс» Эйнштейна, Подольского и Розена
- Эксперименты с фотонами: проблема для специальной теории относительности?
- Уравнение Шредингера; уравнение Дирака
- Квантовая теория поля
- Кошка Шредингера
- Различные точки зрения на существующую квантовую теорию
- К чему мы пришли после всего сказанного?
- Эксперименты с фотонами: проблема для специальной теории относительности?
- Установка значений спин-счетчиков
- Спин-блокировки
- Другие средства работы со спин-блокировками
- Спин-блокировки и обработчики нижних половин
- Спин-блокировки чтения-записи
- Сравнение спин-блокировок и семафоров
- Настройка спин-счетчика
- Настройка производительности SMP-систем с помощью спин-счетчиков
- Приемы софистики и спин-контроля
- Объекты с большим спином
- Эффект спинового эха




