Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Спин и сфера Римана состояний
Спин и сфера Римана состояний
Величину, которую в квантовой механике принято называть «спином», иногда считают самой «квантовомеханической» из всех физических величин, поэтому мы поступим разумно, уделив ей некоторое внимание. Что такое спин? По существу, спин — это мера, характеризующая вращение частицы. Термин «спин»[153] действительно наводит на мысль о чем-то, напоминающем вращение крикетного шара или бейсбольного мяча. Вспомним понятие углового момента, который, подобно энергии и импульсу, является сохраняющейся величиной (см. главу 5 «Динамика Галилея и Ньютона», а также Главу 6 «Начало квантовой теории»). Угловой момент тела остается постоянным во времени до тех пор, пока движение тела не возмущает трение или какие-нибудь другие силы. Он и есть то, чем на самом деле является квантовомеханический спин, но сейчас нас интересует «вращение» отдельной частицы самой по себе, а не обращение по орбитам мириад частиц вокруг общего центра масс (как это было бы в случае крикетного шара). Замечательный физический факт состоит в том, что большинство частиц, обнаруживаемых в Природе, действительно совершают «вращение» в только что указанном смысле, причем каждая частица обладает спином, величина которого специфична только для нее[154]. Но, как мы увидим дальше, спин отдельной квантовомеханической частицы обладает некоторыми весьма экстравагантными свойствами, — совсем не теми, которые мы могли бы ожидать, исходя из своего опыта обращения с закрученным крикетными шарами.
Прежде всего, для частиц определенного типа величина спина всегда одна и та же. Изменяться (причем очень странным образом, о чем мы вскоре узнаем) может только направление спина. Это резко контрастирует с крикетным шаром, который может быть закручен всеми возможными способами как угодно сильно или слабо в зависимости от того, как он был запущен! Для электрона, протона или нейтрона величина спина всегда равна ?/2, т. е. ровно половине наименьшего положительного значения, которое по Бору было изначально допустимым для квантованной величины углового момента атомов. (Напомним, что допустимыми значениями были 0, ?, 2?, 3? ….) Здесь же нам требуется половина фундаментальной единицы ?, и, в некотором смысле, ?/2 сама по себе есть даже более фундаментальная единица. Такая величина углового момента не была бы допустима для объекта, состоящего только из орбитальных частиц, не вращающихся самих по себе. Такая величина может возникнуть только потому, что спин — это внутренне присущее свойство самой частицы (т. е. он не является результатом орбитального движения ее «частей» вокруг некоторого центра).
Частица со спином, равным нечетному кратному ?/2 (т. е. ?/2, 3?/2 или 5?/2 и т. д.) называется фермионом и обладает любопытной квантовомеханической особенностью: полный поворот на 360° переводит ее вектор состояния не в себя, а в себя со знаком минус! Многие частицы, встречающиеся в природе, относятся к числу фермионов, и мы еще узнаем позднее о них и их необычных свойствах, столь жизненно важных для нашего существования. Остальные частицы со спином, равным четному кратному ?/2, т. е. целому кратному ? (а именно 0, ?, 2?, 3?…), называются бозонами. При повороте на 360° вектор состояния бозона переходит точно в себя.
Рассмотрим частицу с половинным спином, т. е. со значением спина ?/2. Для определенности я буду называть такую частицу электроном, но ею с таким же успехом мог бы быть протон или нейтрон, а также атом подходящего вида. («Частица» может состоять из отдельных частей, если ее можно рассматривать квантовомеханически как единое целое с вполне определенным полным угловым моментом.) Предположим, что наш электрон покоится, и рассмотрим только его спиновое состояние. Пространство квантовомеханических состояний (гильбертово пространство) оказывается в этом случае двумерным, поэтому мы можем выбрать базис, состоящий всего лишь из двух состояний. Я обозначу их |?) и |?), чтобы указать, что в состоянии |?) спин вращается слева направо относительно вертикального направления снизу вверх, в то время как в состоянии |?) спин вращается слева направо относительно вертикального направления сверху вниз (рис. 6.24).
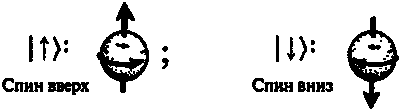
Рис. 6.24. Базис спиновых состояний электрона состоит всего лишь из двух состояний. В качестве них принято выбирать состояния спин вверх и спин вниз
Состояния |?) и |?) взаимно ортогональны, и мы считаем их нормализованными (|?|2 и |?|2 = 1). Любое возможное состояние спина электрона представимо в виде линейной суперпозиции, например, ?|?) + z|?), именно этих двух ортонормированных состояний |?) и |?), т. е. состояний спин вверх и спин вниз.
Нужно сказать, что в состояниях спин вверх и спин вниз нет ничего особенного. С тем же успехом мы могли бы описывать спин, вращающийся слева направо вокруг любого другого направления, например, слева-направо |?) и противоположного ему справа-налево |?). Тогда (при подходящем выборе комплексных весов) мы получили бы для |?) и |?) [155]:
|?) = |?) + |?) и |?) = |?) — |?).
Это позволяет нам по-новому взглянуть на ситуацию. Любое спиновое состояние электрона есть линейная суперпозиция двух ортогональных состояний |?) и |?),т. е. спинов направо и налево. Можно выбрать какое-нибудь совершенно произвольное направление, например, вектор состояния.

Он также является линейной комбинацией спинов |?) и |?) с некоторыми комплексными коэффициентами, скажем,
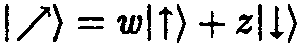
а любое спиновое состояние было бы представимо в виде линейной комбинации этого состояния

и ортогонального ему[156] состояния
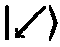
(Заметим, что понятие «ортогональный» в гильбертовом пространстве не обязательно означает «образующий прямой угол с…» в обычном пространстве. Ортогональные вектора состояния в гильбертовом пространстве в данном случае соответствуют диаметрально противоположным направлениям, а не образующим друг с другом прямой угол.)
Каково геометрическое соотношение между направлением в пространстве, определяемым спином

и двумя комплексными числами ? и z? Так как физическое состояние, задаваемое спином

останется неизменным, если мы умножим

на любое ненулевое комплексное число, то значение имеет только отношение числа z к числу ?. Обозначим это отношение через
q = z/? .
Тогда q будет обычным комплексным числом за исключением того, что теперь ему разрешено принимать значение q = ?, чтобы не упускать из рассмотрения ситуацию с ? = 0, т. е. когда спин направлен вертикально вниз. Если q ? ?, то мы можем представить q как точку на плоскости Аргана, как мы делали это в главе 3. Представим себе, что эта плоскость Аргана расположена горизонтально в пространстве, причем действительная ось направлена вправо в вышеуказанном смысле (т. е. в направлении спинового состояния |?) ). Представим теперь сферу единичного радиуса, центр которой совпадает с началом координат плоскости Аргана, а точки 1, i, — 1, -i лежат на экваторе этой сферы. Рассмотрим точку, совпадающую с южным полюсом этой сферы, который мы обозначим ?. Осуществляя проекцию из южного полюса, мы отобразим всю плоскость Аргана на нашу единичную сферу. В результате любая точка q на плоскости Аргана окажется поставленной в соответствие единственной точке q на этой сфере, лежащей на прямой, соединяющей эти две точки с южным полюсом (рис. 6.25).
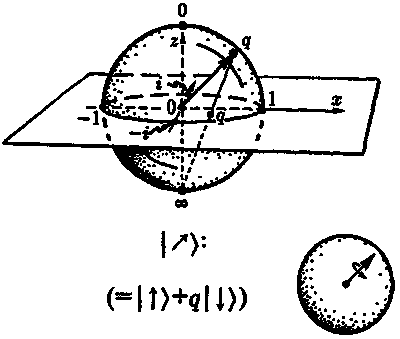
Рис. 6.25. Сфера Римана, представленная как пространство физически различных спиновых состояний частицы со спином 1/2. Сфера Римана стереографически спроецирована из ее южного полюса (?) на плоскость Аргана, проходящую через экватор сферы
Такое соответствие называется стереографической проекцией и обладает многими красивыми геометрическими свойствами (например, сохраняет углы и отображает окружности в окружности). Такая проекция позволяет нам параметризовать точки сферы комплексными числами вместе с ?, т. е. множеством возможных комплексных отношений q. Сфера, параметризованная таким образом, называется сферой Римана. Геометрический смысл сферы Римана для спиновых состояний электрона состоит в том, что направление спина, задаваемое соотношением
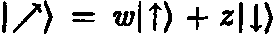
определяется реальным направлением из центра в точку q = z/?, как показано на изображении сферы Римана. Заметим, что северный полюс соответствует состоянию |?), задаваемому соотношением z = 0, т. е. q = 0, а южный полюс — состоянию |?), задаваемому соотношением ? = 0, т. е. q = ?. Самая правая точка сферы Римана помечена значением q = 1, что соответствует состоянию |?) = |?) + |?) а самая левая точка сферы Римана соответствует q = -1, что дает спиновое состояние |?) = |?) — |?). Самая дальняя задняя точка сферы Римана помечена значением q = i, соответствующим состоянию |?) + i |?), в котором спин направлен прямо от нас, а самая близкая точка сферы Римана помечена значением q = — i, соответствующим состоянию |?) — i |?), в котором спин направлен прямо к нам. Произвольная точка, помеченная q, соответствует состоянию |?) + q |?).
Как все это связано с измерением, которое можно было бы произвести над спином электрона?[157] Выберем некоторое направление в пространстве и обозначим его а. Если мы измеряем спин электрона в этом направлении, то ответ ДА означает, что электрон (теперь) действительно вращается слева направо вокруг направления а, в то время как ответ НЕТ означает, что электрон вращается слева направо вокруг направления, противоположного ?.
Предположим, что мы получили ответ ДА, и обозначим результирующее состояние |?). Если мы просто повторим измерение, используя в точности такое же направление ?, как прежде, то с вероятностью 100 % обнаружим, что ответ будет ДА. Но если при втором измерении мы изменим направление и выберем новое направление ?, то обнаружим, что вероятность ответа ДА (состояние перепрыгивает в |?)) будет несколько меньшей, и существует некоторая возможность появления во втором измерении ответа НЕТ (состояние перепрыгивает в направление, противоположное ?). Как нам вычислить эту вероятность? Ответ на этот вопрос содержится в предписаниях, приведенных в конце предыдущего раздела. Вероятность ответа ДА для второго измерения оказывается равной
1/2(1+cos v)
где v — угол между направлениями[158] ? и ?. Соответственно, вероятность ответа НЕТ для второго измерения равна
1/2(1 — cos v)
Отсюда видно, что если второе измерение производится под прямым углом к первому, то вероятность составляет 50 % в обоих случаях (cos 90° = 0); результат второго измерения полностью случаен! Если угол между двумя измерениями острый, то ответ ДА более вероятен, чем ответ НЕТ. Если этот угол — тупой, то ответ НЕТ более вероятен, чем ДА. В предельном случае, когда направление ? противоположно направлению ?, вероятность равна 0 для ответа ДА и 100 % для ответа НЕТ, т. е. результат второго измерения заведомо обратен результату первого измерения. (См. Фейнман и др. [1965] для дальнейшего знакомства со спином.)
Сфера Римана действительно играет фундаментальную (но не всегда признанную) роль в любой квантовой системе с двумя состояниями, описывая (с точностью до коэффициента пропорциональности) набор возможных квантовых состояний. Для частицы с полуцелым спином ее геометрическая роль особенно очевидна, так как точки сферы соответствуют возможным пространственным направлениям спиновых осей.
Увидеть роль сферы Римана во многих других ситуациях труднее. Рассмотрим фотон, только что прошедший через две щели или отразившийся от полупосеребренного зеркала. Состояние фотона есть некоторая линейная комбинация типа
|?t) + |?b), |?t) — |?b) или |?t) + i |?b)
двух состояний |?t) и |?b), описывающих две совершенно различные локализации. Сфера Римана по-прежнему описывает набор физически различных возможностей, но теперь лишь абстрактно. Состояние |?t) представлено северным полюсом («верхушкой») сферы, а состояние |?b) — южным полюсом («дном») сферы. Соответственно, состояния |?t) + |?b), |?t) — |?b) и |?t) + i |?b) представлены различными точками на экваторе, и в общем случае состояние ?|?t) + z|?b) представлено точкой, задаваемой отношением q = z/?. Во многих случаях (как и в рассматриваемом примере) возможности «богатства сферы Римана» довольно глубоко упрятаны, не имея прямого отношения к геометрии пространства!
- Нужна ли философам квантовая теория?
- Проблемы с классической теорией
- Начало квантовой теории
- Эксперимент с двумя щелями
- Амплитуды вероятностей
- Квантовое состояние частицы
- Принцип неопределенности
- Эволюционные процедуры U и R
- Одна частица — сразу в двух местах?
- Гильбертово пространство
- Измерения
- Спин и сфера Римана состояний
- Объективность и измеримость квантовых состояний
- Копирование квантового состояния
- Спин фотона
- Объекты с большим спином
- Многочастичные системы
- «Парадокс» Эйнштейна, Подольского и Розена
- Эксперименты с фотонами: проблема для специальной теории относительности?
- Уравнение Шредингера; уравнение Дирака
- Квантовая теория поля
- Кошка Шредингера
- Различные точки зрения на существующую квантовую теорию
- К чему мы пришли после всего сказанного?
- Спин фотона
- Новаторская сфера
- Установка значений спин-счетчиков
- Оформление состояний hover и focus
- Спин-блокировки
- Другие средства работы со спин-блокировками
- Спин-блокировки и обработчики нижних половин
- Спин-блокировки чтения-записи
- Сравнение спин-блокировок и семафоров
- Настройка спин-счетчика
- Настройка производительности SMP-систем с помощью спин-счетчиков
- Решение проблемы долговременных состояний в многопоточной среде




