Книга: Учебное пособие по курсу «Нейроинформатика»
Функциональная предобработка
Функциональная предобработка
Функциональная предобработка преследует единственную цель — снижение константы Липшица задачи. В разделе «Предобработка, облегчающая обучение», был приведен пример такой предобработки. Рассмотрим общий случай функциональной предобработки, отображающих входной признак x в k-мерный вектор z. Зададимся набором из k чисел, удовлетворяющих следующим условиям: xmin<y1<…<yk-1<yk<xmax.
Таблица 9. Пример функциональной предобработки числового признака x?[0,5], при условии, что сигналы нейронов принадлежат интервалу [-1,1]. В сигмоидной предобработке использована ?(x)=x/(1+|x|), а в шапочной — ?(x)=2/(1+x?)-1. Были выбраны четыре точки yi=i.
| x | z1(x) | z2(x) | z3(x) | z4(x) |
|---|---|---|---|---|
| Линейная предобработка | ||||
| 1.5 | 0.5 | -0.5 | -1 | -1 |
| 3.5 | 1 | 1 | 0.5 | -0.5 |
| Сигмоидная предобработка | ||||
| 1.5 | 0.3333 | -0.3333 | -0.6 | -0.7142 |
| 3.5 | 0.7142 | 0.6 | 0.3333 | -0.3333 |
| Шапочная предобработка | ||||
| 1.5 | 0.6 | 0.6 | -0.3846 | -0.7241 |
| 3.5 | -0.7241 | -0.3846 | 0.6 | 0.6 |
Пусть ? — функция, определенная на интервале [xmin-yk, xmax-y1], а ?min,?max — минимальное и максимальное значения функции ? на этом интервале. Тогда i-я координата вектора z вычисляется по следующей формуле:
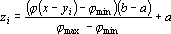
Линейная предобработка. В линейной предобработке используется кусочно линейная функция:
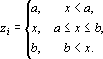
Графики функций zi(x) представлены на рис. 2а. Видно, что с увеличением значения признака x ни одна функция не убывает, а их сумма возрастает. В табл. 9 представлены значения этих функций для двух точек — x1=1.5 и x2=3.5.
Сигмоидная предобработка. В сигмоидной предобработке может использоваться любая сигмоидная функция. Если в качестве сигмоидной функции использовать функцию S2, приведенную в разделе «Нейрон» этой главы, то формула (17) примет следующий вид:
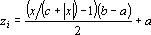
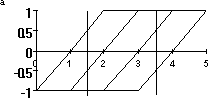
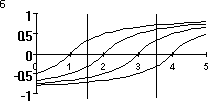

Графики функций zi(x) представлены на рис. 2б. Видно, что с увеличением значения признака x ни одна функция не убывает, а их сумма возрастает. В табл. 9 представлены значения этих функций для двух точек x1=1.5 и x2=3.5.
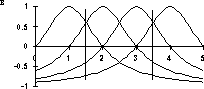
Шапочная предобработка. Для шапочной предобработки используются любые функции, имеющие график в виде «шапочки». Например, функция ?(x)=1/(1+x?).
Графики функций zi(x) представлены на рис. 2 в. Видно, что с увеличением значения признака x ни одна из функций zi(x) , ни их сумма не ведут себя монотонно. В табл. 9 представлены значения этих функций для двух точек x1=1.5 и x2=3.5.
- Модулярная предобработка
- Межфункциональная координация
- Глава 4 Функциональная модель
- Позиционная предобработка
- Функциональная декомпозиция
- Простейшая предобработка числовых признаков
- Предобработка, облегчающая обучение
- 4.4. «Три в одном»: многофункциональная программа Advanced Archive Repair
- 4.19.1 Концепция интерфейса SPIФункциональная схема обмена между двумя контроллерами SPI
- Межфункциональная перестройка и интеграция
- Функциональная структура
- Функциональная совместимость




