Книга: Учебное пособие по курсу «Нейроинформатика»
Другие способы предобработки числовых признаков
В данном разделе будет рассмотрено три вида предобработки числовых признаков — модулярный, позиционный и функциональный. Основная идея этих методов предобработки состоит в том, чтобы сделать значимыми малые отличия больших величин. Действительно, пусть для ответа существенно изменение величины признака на единицу при значении признака порядка миллиона. Очевидно, что простейшая предобработка (1) сделает отличие в единицу неразличимым для нейронной сети при абсолютных значениях порядка миллиона.
Все эти виды предобработки обладают одним общим свойством — за счет кодирования входного признака несколькими сигналами они уменьшают сложность задачи (критерий Липшица).
Модулярная предобработка
Зададимся некоторым набором положительных чисел y1, …, yk. Определим сравнение по модулю для действительных чисел следующим образом:
x mod y = x-y?Int(x/y), (15)
где Int(x) — функция, вычисляющая целую часть величины x путем отбрасывания дробной части. Очевидно, что величина x mod y лежит в интервале (-y, y).
Кодирование входного признака x при модулярной предобработке вектором Z производится по следующей формуле:
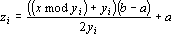
Таблица 8. Пример сигналов при модулярном вводе
| x | x mod 3 | x mod 5 | x mod 7 | x mod 11 |
|---|---|---|---|---|
| 5 | 2 | 0 | 5 | 5 |
| 10 | 1 | 0 | 3 | 10 |
| 15 | 0 | 0 | 1 | 3 |
Однако модулярная предобработка обладает одним отрицательным свойством — во всех случаях, когда yi?yr1, при целом r, разрушается отношение предшествования чисел. В табл. 8 приведен пример векторов. Поэтому, модульная предобработка пригодна при предобработке тех признаков, у которых важна не абсолютная величина, а взаимоотношение этой величины с величинами y1, …, yk.
Примером такого признака может служить угол между векторами, если в качестве величин y выбрать yi=?/i.
Функциональная предобработка
Функциональная предобработка преследует единственную цель — снижение константы Липшица задачи. В разделе «Предобработка, облегчающая обучение», был приведен пример такой предобработки. Рассмотрим общий случай функциональной предобработки, отображающих входной признак x в k-мерный вектор z. Зададимся набором из k чисел, удовлетворяющих следующим условиям: xmin<y1<…<yk-1<yk<xmax.
Таблица 9. Пример функциональной предобработки числового признака x?[0,5], при условии, что сигналы нейронов принадлежат интервалу [-1,1]. В сигмоидной предобработке использована ?(x)=x/(1+|x|), а в шапочной — ?(x)=2/(1+x?)-1. Были выбраны четыре точки yi=i.
| x | z1(x) | z2(x) | z3(x) | z4(x) |
|---|---|---|---|---|
| Линейная предобработка | ||||
| 1.5 | 0.5 | -0.5 | -1 | -1 |
| 3.5 | 1 | 1 | 0.5 | -0.5 |
| Сигмоидная предобработка | ||||
| 1.5 | 0.3333 | -0.3333 | -0.6 | -0.7142 |
| 3.5 | 0.7142 | 0.6 | 0.3333 | -0.3333 |
| Шапочная предобработка | ||||
| 1.5 | 0.6 | 0.6 | -0.3846 | -0.7241 |
| 3.5 | -0.7241 | -0.3846 | 0.6 | 0.6 |
Пусть ? — функция, определенная на интервале [xmin-yk, xmax-y1], а ?min,?max — минимальное и максимальное значения функции ? на этом интервале. Тогда i-я координата вектора z вычисляется по следующей формуле:
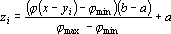
Линейная предобработка. В линейной предобработке используется кусочно линейная функция:
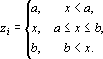
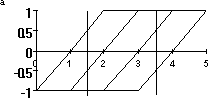
Графики функций zi(x) представлены на рис. 2а. Видно, что с увеличением значения признака x ни одна функция не убывает, а их сумма возрастает. В табл. 9 представлены значения этих функций для двух точек — x1=1.5 и x2=3.5.
Сигмоидная предобработка. В сигмоидной предобработке может использоваться любая сигмоидная функция. Если в качестве сигмоидной функции использовать функцию S2, приведенную в разделе «Нейрон» этой главы, то формула (17) примет следующий вид:
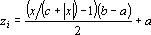
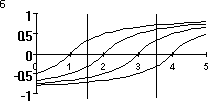

Графики функций zi(x) представлены на рис. 2б. Видно, что с увеличением значения признака x ни одна функция не убывает, а их сумма возрастает. В табл. 9 представлены значения этих функций для двух точек x1=1.5 и x2=3.5.
Шапочная предобработка. Для шапочной предобработки используются любые функции, имеющие график в виде «шапочки». Например, функция ?(x)=1/(1+x?).
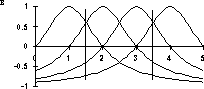
Графики функций zi(x) представлены на рис. 2 в. Видно, что с увеличением значения признака x ни одна из функций zi(x) , ни их сумма не ведут себя монотонно. В табл. 9 представлены значения этих функций для двух точек x1=1.5 и x2=3.5.
- Простейшая предобработка числовых признаков
- Другие инструменты для осуществления резервного копирования
- Другие изменения в 7-й версии InterBase
- Определение пользовательского формата числовых данных
- Датчик расположения и другие датчики
- 6.4 Другие файловые системы
- Глава 3 Способы монетизации
- Способы «запуска» слухов
- Другие предикаты сравнения
- Я установил программу и не хочу, чтобы другие пользователи о ней знали. Как скрыть ее?
- Можно ли интегрировать в пакет установки Windows Service Pack и другие обновления, чтобы потом не приходилось их устанав...
- Другие варианты подключения




