Книга: Учебное пособие по курсу «Нейроинформатика»

Модель линейных зависимостей

Модель линейных зависимостей

Это первая модель, которая может быть решена методом динамических ядер, но не может быть получена с помощью обучения сети Кохонена, поскольку ядра не являются точками в пространстве объектов. Ядрами в данной модели являются прямые, а мерой близости — квадрат расстояния от точки (объекта) до прямой. Прямая в n—мерном пространстве задается парой векторов: aⁱ = (bⁱ, cⁱ). Первый из векторов задает смещение прямой от начала координат, а второй является направляющим вектором прямой. Точки прямой задаются формулой x = b + tc, где t — параметр, пробегающий значения от минус бесконечности до плюс бесконечности. t имеет смысл длины проекции вектора x-b на вектор c. Сама проекция равна tc. При положительном значении вектор проекции сонаправлен с вектором c, при отрицательном — противоположно направлен. При условии, что длина вектора c равна единице, проекция вычисляется как скалярное произведение (x–b,c). В противном случае скалярное произведение необходимо разделить на квадрат длины c. Мера близости вектора (точки) x определяется как квадрат длины разности вектора x и его проекции на прямую. При решении задачи (4) необходимо найти минимум следующей функции:

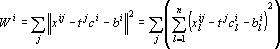
Продифференцируем целевую функцию по неизвестным t^q, cⁱ_r, bⁱ_r и приравняем результаты к нулю.

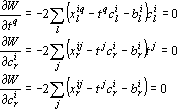
Выразим из последнего уравнения в (10) bⁱ_r:

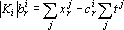
В качестве bⁱ можно выбрать любую точку прямой. Отметим, что для любого набора векторов x^ij и любой прямой с ненулевым направляющим вектором cⁱ на прямой найдется такая точка bⁱ, что сумма проекций всех точек на прямую x = b + tc будет равна нулю. Выберем в качестве bⁱ такую точку. Второе слагаемое в правой части (11) является r-й координатой суммы проекций всех точек на искомую прямую и, в силу выбора точки bⁱ равно нулю. Тогда получаем формулу для определения bⁱ:

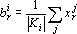
Из первых двух уравнений (10) получаем формулы для определения остальных неизвестных:

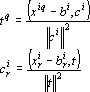
Поиск решения задачи (4) для данного вида классификации осуществляется по следующему алгоритму:

1. Вычисляем bⁱ по формуле (12).

2. Вычисляем t по первой формуле в (13).

3. Вычисляем cⁱ по второй формуле в (13).

4. Если изменение значения cⁱ превышает заданную точность, то переходим к шагу 2, в противном случае вычисления закончены.

Оглавление книги