Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Черные дыры
Черные дыры
Начнем с теоретических предсказаний дальнейшей судьбы нашего Солнца. К настоящему моменту оно уже просуществовало около пяти миллиардов лет. В ближайшие 5–6 миллиардов лет оно начнет увеличиваться в размерах и будет непрерывно раздуваться до тех пор, пока его поверхность не достигнет где-то орбиты Земли. Тогда оно превратится в звезду, называемую красным гигантом. На небосводе можно обнаружить множество красных гигантов, из которых наиболее известны Альдебаран в созвездии Тельца и Бетельгейзе в созвездии Ориона. Пока поверхность красного гиганта расширяется, в самой его сердцевине находится чрезвычайно плотная концентрация материи, которая непрерывно увеличивается в размерах. Это плотное ядрышко имеет ту же природу, что и звезда, называемая белым карликом (рис. 7.12).
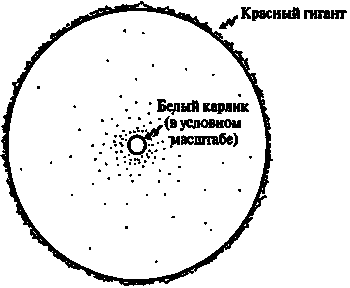
Рис. 7.12. Красный гигант с белым карликом в своей сердцевине
Сами по себе белые карлики — это самые настоящие звезды, вещество которых, правда, спрессовано до такой степени, что теннисный шарик, заполненный им, весил бы несколько сотен тонн! Их число на небосводе довольно велико: примерно десять процентов всех светящихся звезд Млечного Пути приходится на белые карлики. Самый знаменитый из них — спутник Сириуса, чья невообразимо высокая плотность представляла большую загадку для наблюдательной астрономии в начале XX века. Однако позже именно эта звезда превосходным образом подтвердила справедливость физической теории (выдвинутой P. X. Фаулером примерно в 1926 году), согласно которой некоторые звезды и в самом деле могут обладать колоссальной плотностью, при которой они удерживаются в равновесии «давлением электронного вырождения». Это означает, что от гравитационного коллапса такую звезду спасает только квантовомеханический принцип запрета Паули (гл.5 «Многочастичные системы» примеч.163), примененный к электронам.
Любой красный гигант имеет ядро в виде белого карлика, и это ядро постоянно затягивает в себя вещество из основного тела звезды. В конце концов, красный гигант будет целиком поглощен своим ядром-паразитом и в результате останется самый настоящий белый карлик размером с Землю. Что касается нашего Солнца, то оно будет находиться в стадии красного гиганта «всего лишь» несколько миллиардов лет. После этого, в своем последнем «видимом» воплощении, Солнце станет похожим на тлеющие и медленно остывающие угли[180] белого карлика, и просуществует еще несколько миллиардов лет до тех пор, пока окончательно не превратится в совершенно невидимый черный карлик.
Далеко не все звезды повторяют судьбу Солнца. У некоторых из них жизненный путь имеет гораздо более бурный характер и определяется так называемым пределом Чандрасекара: максимально возможной массой белого карлика. Согласно вычислениям, проведенным еще в 1929 году Субраманьяном Чандрасекаром, белые карлики не могут существовать, если их масса превышает шесть пятых массы Солнца! (В то время он был еще совсем молодым индийским студентом, и свои вычисления делал во время морского путешествия из Индии в Англию.) Затем, где-то в 1930 году, эти вычисления были проделаны (независимо) еще раз советским теоретиком Львом Давидовичем Ландау. Современное уточненное значение предела Чандрасекара составляет примерно
1,4 M?
где М? — масса Солнца.
Заметим, что предел Чандрасекара совсем ненамного превосходит солнечную массу, и в то же время известно множество звезд, обладающих значительно бо?льшими массами. А как сложится судьба звезды, обладающей массой, скажем, 2М?? В соответствии с принятой теорией, такая звезда будет так же раздуваться и превратится в красный гигант, а ее ядро — белый карлик — будет постепенно набирать свою массу, — т. е. в точности так, как было описано выше. Однако, в некоторый критический момент, это ядро достигнет предела Чандрасекара, и принцип запрета Паули уже не сможет обеспечить давление, необходимое для компенсации чудовищных сил гравитации[181]. Примерно в этот момент ядро начнет катастрофически коллапсировать внутрь, что приведет, в свою очередь, к значительному повышению давления и температуры. Начнутся интенсивные ядерные реакции, и колоссальное количество энергии выделится из ядра в виде нейтрино. Они разогреют внешнюю оболочку коллапсирующей звезды, а затем последует грандиозный взрыв. Звезда превратится в сверхновую!
А что произойдет далее со все еще коллапсирующим ядром? Теория утверждает, что оно достигнет таких немыслимых плотностей, которые намного превосходят даже плотность белого карлика. Тогда коллапс ядра остановится и оно станет нейтронной звездой (см. выше «Источник низкой энтропии во Вселенной»), в которой теперь уже давление нейтронного вырождения (т. е. принцип Паули, примененный к нейтронам) будет удерживать ее в равновесии. Ее плотность такова, что теннисный мячик, сделанный из вещества нейтронной звезды, весил бы как астероид Гермес (или как марсианская луна Демос). Такую плотность имеет само ядерное вещество! (По сути дела, можно сказать, что нейтронная звезда представляет собой гигантское атомное ядро, радиусом с десяток километров, что, впрочем, совсем немного по звездным меркам!) Но здесь вступает в силу новый предел, аналогичный пределу Чандрасекара (и называемый пределом Ландау-Оппенгеймера-Волкова), который приближенно (по уточненным современным данным) составляет
2,5 М?,
и по превышении которого равновесие нейтронной звезды невозможно.
А что случится с коллапсирующим ядром, если масса исходной звезды будет настолько велика, что даже и этот предел будет превышен? Кстати говоря, известно много звезд, масса которых заключена в пределах от 10М? до 100M?. Маловероятно, что все они в процессе взрыва сверхновой сбрасывают столь большую массу, что ядро-остаток неизменно оказывается с массой ниже верхнего предела для нейтронной звезды. Вместо этого мы, скорее всего, получим черную дыру.
Что же такое черная дыра? Это — область пространства (или пространства-времени), в пределах которой гравитационное поле настолько сильно, что даже свет не способен вырваться из нее. Вспомним, что в силу принципа относительности скорость света является предельной: ни один материальный объект или сигнал не может превысить ее локальное значение (Глава 5. «Специальная теория относительности Эйнштейна и Пуанкаре»). Следовательно, если даже свет не может вырваться из черной дыры, то из нее не сможет выбраться наружу вообще ничего.
Читатель, возможно, знаком с понятием второй космической скорости. Это та минимальная начальная скорость, которую должен иметь объект, чтобы он мог удалиться от некоторого массивного тела на сколь угодно большое расстояние. Пусть массивное тело — это Земля, тогда вторая космическая скорость для нее будет составлять примерно 40000 км/ч (километров в час). Камень, брошенный с земной поверхности (в любом направлении) со скоростью, превышающей это значение, навсегда покинет Землю (мы, конечно, пренебрегаем силами сопротивления земной атмосферы). Если же камень бросить со скоростью, меньшей этого значения, он упадет обратно на Землю. (Поэтому неверно утверждение, что «все брошенное вверх, обязательно упадет вниз»; это будет справедливым только в том случае, когда скорость бросания меньше второй космической!) Для Юпитера вторая космическая скорость равна 220 000 км/ч; а для Солнца она будет составлять уже 2 200 000 км/ч. Теперь представим себе, что вся солнечная масса оказалась сосредоточенной в сфере радиуса в одну четверть от его истинного значения. В этом случае вторая космическая скорость увеличится в два раза по сравнению с исходным значением. А если бы вся масса Солнца оказалась сосредоточенной в еще меньшем объеме, скажем, внутри сферы радиуса в одну сотую от его истинного значения, вторая космическая скорость увеличилась бы в десять раз. Мы можем представить себе, таким образом, достаточно массивное тело малых размеров, для которого вторая космическая скорость превышает даже скорость света! Когда это происходит в действительности, мы и имеем черную дыру[182]
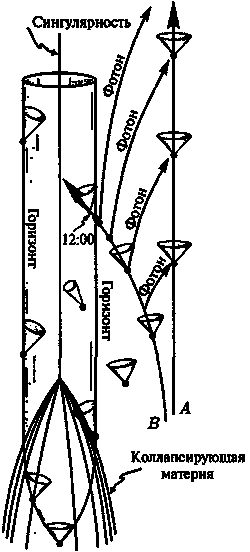
Рис. 7.13. Пространственно-временна?я диаграмма, демонстрирующая коллапс в черную дыру. Шварцшильдовский радиус обозначен как «горизонт»
На рис. 7.13 я изобразил пространственно-временну?ю диаграмму, показывающую коллапс тела, который приводит к образованию черной дыры (для простоты я предположил, что в процессе коллапса сохраняется сферическая симметрия тела и убрал одно пространственное измерение). На рисунке изображены также световые конусы, которые, как мы помним из обсуждения общей теории относительности в главе 5 (см. Глава 5. «Общая теория относительности Эйнштейна» рис. 5.29), абсолютным образом ограничивают допустимые движения тел и распространение сигналов. Заметим, что эти конусы начинают немного наклоняться внутрь и чем ближе к центру, тем этот наклон становится более и более значительным.
Существует некоторое критическое расстояние от центра, называемое шварцшильдовским радиусом, на котором внешние границы конусов становятся вертикальными на приведенной диаграмме. Здесь свет (который по определению должен двигаться по световому конусу) как бы зависает над коллапсирующим телом, а составляющей скорости света, направленной наружу, едва-едва хватает на то, чтобы противодействовать гигантским силам притяжения. Та трехмерная поверхность, которая вычерчивается зависшим светом на шварцшильдовском радиусе (т. е. вся световая история) носит название (абсолютного) горизонта событий черной дыры. Все, что находится внутри горизонта событий, не может выйти наружу и даже не может иметь какой-либо связи с внешним миром. Это заключение является прямым следствием наклона конусов и того фундаментального факта, что возможное движения и распространение сигналов может осуществляться только внутри (или вдоль) этих конусов. Черная дыра, образовавшаяся из начальной звезды массой, равной нескольким массам солнца, будет иметь горизонт радиусом несколько километров. Есть некоторые основания предполагать, что в центрах галактик могут находиться черные дыры гораздо больших масс и размеров. Наша собственная Галактика, которую мы наблюдаем на небе как Млечный Путь, вполне может содержать черную дыру, имеющую массу около миллиона солнечных масс и, следовательно, радиус горизонта — несколько миллионов километров.
Реальное материальное тело, которое коллапсирует с образованием черной дыры, в конце концов, целиком окажется внутри своего горизонта и, следовательно, потеряет всякую связь с внешним миром. Далее мы в общих чертах проследим вероятную судьбу этого тела, а в данный момент для нас будет представлять интерес только геометрия пространства-времени, порожденная этим коллапсом, которая приводит к весьма любопытным следствиям.
Вообразим, что некий отважный (а, может быть, безрассудный?) астронавт В собрался совершить путешествие в нутро большой черной дыры, а его менее смелый (а, может быть, просто более осторожный?) коллега А остается при этом за пределами горизонта событий. Предположим, что А намеревается держать В в поле своего зрения до тех пор, пока это в принципе возможно. Что же увидит А? Глядя на рис. 7.13, нетрудно сообразить, что ту часть истории В (т. е. мировой линии В), которая лежит внутри горизонта, А не увидит никогда, в то время как часть, лежащую снаружи горизонта, А рано или поздно увидит целиком, хотя те точки истории В, которые непосредственно предшествуют моменту его прохождения через горизонт, будут наблюдаться А спустя все большее и большее время ожидания. Пусть В проходит горизонт в тот момент, когда его собственные часы показывают 12 часов. Само это событие А не зафиксирует никогда, но события, соответствующие показаниям часов
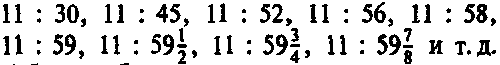
А будет наблюдать совершенно определенно (причем через приблизительно равные интервалы времени по показаниям часов А). В принципе, В будет все время находиться в поле зрения А как бы навечно зависшим над горизонтом черной дыры, а часы В будут отсчитывать время все медленнее и медленнее по мере приближения к роковой отметке 12:00, но никогда не покажут этого значения. Но, в действительности, образ В, который видит А, очень быстро станет неясным и трудноразличимым. Это происходит потому, что образ В, который будет наблюдать А в течение всего оставшегося времени наблюдения, будет формироваться лишь светом, испущенным из того крошечного участка мировой линии В, который непосредственно примыкает извне к горизонту. В результате В просто исчезнет из поля зрения А, и то же самое окажется верным и для исходного коллапсирующего тела. Все, что увидит А, будет выглядеть, в конце концов, действительно как какая-то «черная дыра»!
А что можно сказать о несчастном В? Каковы будут его ощущения? Необходимо сразу же подчеркнуть, что в момент пересечения горизонта с В ничего особенного не произойдет. Он смотрит на свои часы около 12 и видит, что минута за минутой следуют обычным порядком: 11: 57, 11: 58, 11: 59, 12: 00, 12: 01, 12: 02, 12: 03… Промежуток времени около 12: 00 не содержит ничего необычного. В может обернуться, посмотреть на А и убедиться, что А все время остается в поле его зрения. В может также посмотреть на часы А и также убедиться, что для него они идут обычным образом. Таким образом, В никак не может узнать о своем пересечении горизонта, если только не проделает для этого специальных расчетов[183]. Горизонт оказался предельно коварным! После пересечения горизонта, у В уже не остается никаких шансов выйти наружу. Он обнаружит, что окружающая его часть вселенной сжимается, и что довольно скоро ему предстоит испытать свой собственный «большой коллапс»!
А может быть, и не только его собственное. Все вещество того первоначального тела, из которого образовалась черная дыра, будет, в некотором смысле, разделять судьбу В и испытывать такой же коллапс. Более того: в случае, если вселенная снаружи дыры пространственно замкнута, так что вся внешняя материя тоже оказывается вовлеченной в глобальный большой коллапс, то этот коллапс должен оказаться, в определенном смысле, «тем же самым», что и «собственный» коллапс В[184].
Но несмотря на столь безрадостный конец В, физика, с которой он будет иметь дело вплоть до гибельной точки, будет той самой, которую мы с вами хорошо знаем и понимаем. В частности, нет никаких оснований предполагать нарушение второго начала термодинамики, тем более предполагать, что полностью обратится монотонный рост энтропии. Второе начало будет действовать внутри черной дыры точно также, как и везде. Энтропия в окрестности В будет продолжать возрастать, вплоть до самого момента его окончательного коллапса.
Чтобы разобраться, каким образом энтропия «большого коллапса» («собственного» или «всеохватывающего») может быть чрезвычайно высокой, в то время как энтропия большого взрыва может оказаться при этом намного меньше, нам следует немного глубже вникнуть в свойства геометрии пространства-времени черной дыры. Перед тем, как мы этим займемся, читатель должен взглянуть на рис. 7.14, на котором показано гипотетическое временно?е обращение черной дыры, называемое белой дырой.
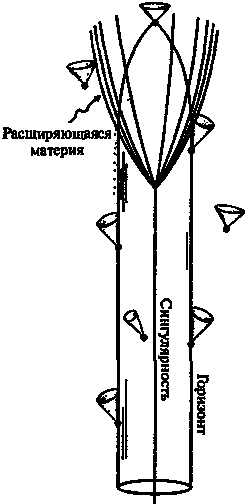
Рис. 7.14. Гипотетическая пространственно-временна?я конфигурация: белая дыра, эволюция которой приводит к расширяющейся материи (эта ситуация является обращением во времени рис. 7.13)
(Скорее всего, белых дыр в природе не существует, но их теоретическая возможность будет иметь для нас большое значение в дальнейшем.)
- Течение времени
- Неумолимое возрастание энтропии
- Что такое энтропия?
- Второе начало в действии
- Источник низкой энтропии во Вселенной
- Космология и Большой взрыв
- Горячий протошар
- Объясняется ли второе начало Большим взрывом?
- Черные дыры
- Структура пространственно-временны?х сингулярностей
- Насколько особым был Большой взрыв?
- Красно-черные деревья
- «Черные комнаты»
- «Черные» и «белые» методы продвижения бизнеса в Интернете
- «Черные» и «белые» методы продвижения бизнеса в интернете
- 4.3. Спам-фильтры и черные списки
- "Дыры" в системе безопасности
- Есть только один способ заткнуть дыры
- Черные солидные ботинки
- Карты помогают вам распознать дыры в истории
- Ищите «дыры» в «песочных часах»
- Черные методы продвижения
- Вычислимость в классической физике: где мы находимся?




