Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Неумолимое возрастание энтропии
Неумолимое возрастание энтропии
Представим себе стакан воды, стоящий на самом краю стола. Если его слегка подтолкнуть, он, скорее всего, упадет на пол, наверняка разобьется вдребезги на множество осколков, а вода расплескается повсюду, возможно, частично поглотившись ковром или просочившись в щели между половицами. Наш стакан воды в этой ситуации лишь добросовестно следует уравнениям физики. Ньютоновское описание оказывается справедливым здесь в полной мере. Каждый из атомов в стекле и в воде подчиняется законам Ньютона (рис. 7.2).
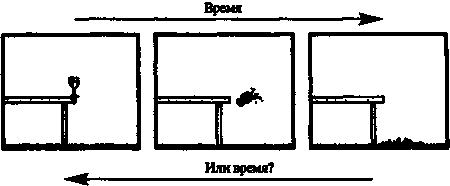
Рис. 7.2. Законы механики обратимы во времени; однако последовательность событий в направлении справа налево никогда не наблюдается, в то время как последовательность слева направо была бы вполне обычной
А теперь попробуем прокрутить эту картину в обратном направлении. В силу обратимости во времени законов Ньютона, вода могла бы также легко истечь из ковра и из щелей в половицах, заполнить стакан, который в это время ловко собирал бы себя из множества отколовшихся осколков, а затем все это могло запрыгнуть на высоту стола и устроиться в равновесии на его краю. И все это, так же как и первоначальный процесс, происходило бы в полном соответствии с законами Ньютона!
Читатель, быть может, спросит, откуда берется энергия, поднявшая стакан с пола на стол. Ответить на этот вопрос совсем несложно, поскольку, в то время, когда стакан падает со стола, энергия, которую он приобретает в процессе падения, должна куда-то деваться. На самом деле, энергия падающего стакана переходит в тепло. Атомы в осколках стакана, в воде, в ковре и половицах после удара стакана о пол будут хаотически колебаться чуть-чуть быстрее, чем до удара, т. е. осколки стакана, вода, ковер и половицы будут чуточку горячее, чем они были раньше (если пренебречь возможной потерей тепла за счет испарения, которое, однако, в принципе тоже обратимо). В силу закона сохранения энергии эта тепловая энергия будет в точности равна той, которая теряется стаканом с водой при его падении со стола. Таким образом, этой маленькой порции тепловой энергии было бы как раз достаточно, чтобы поднять стакан обратно на стол! Очень важно не забыть учесть вклад тепловой энергии в общий энергетический баланс. Закон сохранения энергии, в котором учитывается также и тепловая энергия, носит название первого начала термодинамики. Этот закон, будучи следствием ньютоновской механики, симметричен во времени. Он не накладывает каких-либо ограничений на стакан и воду, которые бы запрещали стакану собирать себя, заполняться водой и таким вот чудесным образом запрыгивать обратно на стол.
Причина, по которой мы не наблюдаем ничего подобного в реальности, заключается в том, что «тепловое» движение атомов в осколках стекла, воде, половицах и ковре является совершенно беспорядочным, так что подавляющая часть атомов будет двигаться во всех возможных направлениях. Необходима невероятно точная координация их движений для того, чтобы восстановить стакан, вместе со всей собранной в него с пола водой, и аккуратно забросить его на стол. Можно даже утверждать, что такие слаженные движения невозможны. Точнее говоря, подобная скоординированность могла бы возникнуть только благодаря удивительной случайности, которую мы все равно отнесли бы к разряду «чудес», даже если бы она и произошла в действительности!
Однако для другого направления времени такая согласованность движений атомов является вполне нормальной. Ведь мы почему-то не относим в разряд случайных те ситуации, в которых частицы движутся скоординированным образом после некоторого крупномасштабного изменения физического состояния (в нашем случае — разбивания стакана и расплескивания воды), а не до такого изменения. Движение частиц после подобного события как раз и должно быть в высокой степени согласованным, поскольку сама природа этого движения такова, что если бы мы могли в точности обратить движение каждого отдельного атома, результирующее движение было бы именно таким, какое необходимо для восстановления, заполнения и подъема стакана в его исходное положение.
Высокая координация движения вполне приемлема и даже естественна в том случае, когда оно является следствием крупномасштабного изменения, а не его причиной. Но слова «причина» и «следствие», так или иначе, затрагивают вопрос о временнбй асимметрии. Используя эти термины в нашем повседневном разговорном языке, мы обычно подразумеваем, что причина должна предшествовать следствию. Но если мы пытаемся осознать физическое различие между прошлым и будущим, нам необходимо быть предельно осторожными, чтобы невольно не привнести в рассуждения наши житейские представления об этих понятиях. Я должен предупредить читателя, что избежать этого чрезвычайно трудно, но нам все же стоит попробовать. Мы должны попытаться использовать слова таким образом, чтобы они заранее не предрешали вопроса о физическом различии прошлого и будущего. В частности, если обстоятельства будут к тому располагать, нам придется иногда рассматривать причины некоторых явлений лежащими в будущем, а следствия — лежащими в прошлом! Детерминистские уравнения классической физики (или операция U в квантовой физике) никоим образом не выделяют эволюцию в направлении будущего. Они могут быть столь же хорошо применимы и для описания эволюции в прошлое. Будущее определяет прошлое точно так же, как и прошлое определяет будущее. Мы можем каким-либо образом зафиксировать некоторое состояние системы в будущем и затем использовать его для определения состояния системы в прошлом. Если, применяя наши уравнения к системе с обычным направлением времени в сторону будущего, мы можем считать прошлое причиной, а будущее — следствием, то в случае, когда мы также правомерно используем эти уравнения для описания эволюции в прошлое, мы будем вынуждены относить будущее к «причине», а прошлое — к «следствию».
Есть, однако, еще один момент, связанный с использованием терминов «причина» и «следствие», который, на самом деле, никак не зависит от того, какие события мы относим к прошлому, а какие — к будущему. Вообразим себе гипотетическую вселенную, в которой справедливы те же симметричные во времени классические уравнения, что и в нашей вселенной, но в которой явления обычного порядка (такие, как разбивание и расплескивание стакана воды) сосуществуют с их обращениями во времени. Предположим, что наряду с обычными явлениями, стаканы воды иногда действительно собирают себя из отколовшихся кусочков, чудесным образом заполняются расплескавшейся водой и затем запрыгивают на стол; предположим также, что иногда, приготовленная яичница-болтунья снова превращается в исходный полуфабрикат, желток в ней отделяется от белка и, наконец, она запрыгивает обратно в сломанную яичную скорлупу, которая становится совершенно целой, вновь заключая в себя все свое содержимое; что кусочки сахара могут восстанавливаться из растворенного сахара в подслащенном кофе и затем самопроизвольно выпрыгивать из чашки прямо в чью-нибудь руку. Если бы мы жили в мире, в котором подобные вещи относились бы к разряду повседневных явлений, мы, очевидно, могли бы приписать «причины» таких событий не фантастической случайности, связанной с коррелированным поведением отдельных атомов, но некоторому «телеологическому воздействию», благодаря которому самовосстанавливающиеся объекты стремятся в конце концов достичь желаемой макроскопической конфигурации. «Смотрите! — могли бы воскликнуть мы. — Это повторяется. Та смесь намеревается собрать себя в другой стакан воды!» Мы, разумеется, можем принять точку зрения, согласно которой атомы направили сами себя именно так, потому что именно таким способом можно получить стакан воды на столе. Стакан на столе был бы в этом случае причиной, а явно беспорядочная смесь атомов на полу — «следствием» — несмотря на то, что это «следствие» теперь существует во времени раньше, чем причина. Точно также, внезапное упорядочивание движения атомов в приготовленной яичнице-болтунье не является «причиной» ее запрыгивания в целую яичную скорлупу, но есть следствие этого будущего состояния; и кусок сахара собирается и выскакивает из чашки не «потому, что» атомы движутся с такой необычайной точностью, но благодаря тому, что кто-то — находящийся в будущем — будет позднее держать этот кусок сахара в своей руке!
Конечно, мы не наблюдаем ничего подобного в нашем мире — или, лучше сказать, что мы не обнаруживаем одновременного сосуществования подобных вещей с явлениями обычного порядка. Ведь если бы все, что мы видели, было бы явлениями обратного порядка, подобного описанному выше, у нас не было бы проблем. Нам нужно было бы просто поменять местами «прошлое» и «будущее», «до» и «после» и т. д. во всех наших описаниях. Время следовало бы тогда считать текущим в направлении обратном по отношению к первоначально выбранному, и такой мир мог бы описываться так же, как и наш. Здесь я, однако, хочу рассмотреть другую возможность, в точности согласующуюся с симметричными во времени уравнениями физики, а именно — когда разбивающийся и самовосстанавливающийся стаканы могут сосуществовать.
В этом мире мы были бы не в состоянии восстановить привычные описания событий одним только изменением наших соглашений о направлении движения времени. Конечно, наш мир оказывается не таким — но почему? Чтобы разобраться с этим, я для начала попросил бы вас представить такой мир и подумать над тем, как описывать события, происходящие в нем. Согласитесь, что в подобном мире мы могли бы хорошо описывать крупные макроскопические конфигурации — такие как полные стаканы воды, неразбитые яйца, или кусочки сахара в руке, являющиеся «причинами»; и микроскопические, быть может, тонко скоррелированные движения отдельных атомов, представляющие «следствия» — независимо от того, лежат ли «причины» в прошлом или будущем своих «следствий».
Почему же в мире, в котором живем мы, именно причины всегда предшествуют следствиям или, иными словами, почему точно скоординированные движения частиц возникают только после крупномасштабных изменений физического состояния, а не перед ними? Чтобы лучше разобраться в таком положении дел, мне нужно ввести понятие энтропии. Грубо говоря, энтропия системы есть мера ее явного беспорядка. (Позже я дам более точное определение.) Таким образом, разбитый стакан и разлитая по полу вода находятся в состоянии с большей энтропией, чем целый заполненный водой стакан на столе. Приготовленная яичница-болтунья обладает большей энтропией, чем свежее неразбитое яйцо; подслащенный кофе обладает большей энтропией, чем кофе с нерастворенным куском сахара в нем. Подобные низкоэнтропийные состояния выглядят как бы «специально упорядоченными» некоторым явным образом, а высокоэнтропийные состояния — менее «специально упорядоченными».
Здесь важно подчеркнуть, что говоря о «специальности» (или, скажем, «особенности») состояния с низкой энтропией, мы, на самом деле, имеем ввиду именно явную «специальность». Если этого не оговорить, то при более детальном рассмотрении мы могли бы увидеть, что высокоэнтропийные состояния в подобных ситуациях будут такими же «специально упорядоченными», как и низкоэнтропийные, благодаря чрезвычайно точной координации движений отдельных частиц. Например, кажущееся случайным движение молекул воды, просочившейся между половицами после того, как стакан разбился, является, на самом деле, вполне специальным: эти перемещения настолько точны, что если их обратить, то получится то самое исходное низкоэнтропийное состояние, в котором восстановленный стакан покоится на столе. (Это должно быть именно так, поскольку обращение всех этих движений полностью соответствует обращению направления времени, в результате которого стакан, разумеется, восстановил бы себя и запрыгнул обратно на стол.) Но подобное скоординированное движение всех молекул воды — совсем не та «специальность», которую мы имеем ввиду, говоря о низкой энтропии. Энтропия относится к явному беспорядку. Порядок же, относящийся к точной координации движений частиц, не есть явный порядок, и потому он не приводит к понижению энтропии системы. Таким образом, упорядочивание молекул разлитой жидкости, в данном случае, не учитывается, и ее энтропия остается высокой. В то же время, явный порядок в восстановленном стакане воды дает низкое значение энтропии. Все дело здесь в том, что с конфигурацией восстановленного и заполненного стакана воды совместимо относительно немного возможных движений частиц; в то время как движений, совместимых с конфигурацией слегка нагретой воды, протекающей между щелями в половицах, — существенно больше.
Второе начало термодинамики гласит, чтоэнтропия изолированной системы возрастает со временем (или остается неизменной в случае обратимых систем). Теперь становится очевидным, что мы совершенно правильно не рассматриваем скоординированное движение частиц как признак низкой энтропии, поскольку в этом случае «энтропия» системы, в соответствии с ее определением, всегда оставалась бы постоянной. Понятие энтропии должно быть связано только с явным беспорядком. Для системы, изолированной от всей остальной вселенной, ее полная энтропия возрастает, так что, если подобная система начинает свою эволюцию из состояния с некоторой явной упорядоченностью, то с течением времени этот порядок неизбежно разрушается и присущие ей особые свойства превращаются в «бесполезно» скоординированное движение частиц.
Может показаться, что второе начало действует как некий предвестник упадка, поскольку оно утверждает существование безжалостного универсального физического принципа, напоминающего нам о том, что всякое упорядоченное состояние подвержено непрерывному разрушению. Позднее мы увидим, что это пессимистическое заключение справедливо не всегда!
- Течение времени
- Неумолимое возрастание энтропии
- Что такое энтропия?
- Второе начало в действии
- Источник низкой энтропии во Вселенной
- Космология и Большой взрыв
- Горячий протошар
- Объясняется ли второе начало Большим взрывом?
- Черные дыры
- Структура пространственно-временны?х сингулярностей
- Насколько особым был Большой взрыв?




