Книга: Фундаментальные алгоритмы и структуры данных в Delphi

Красно-черные деревья

Красно-черные деревья

Рассмотрев простые и спаренные двусторонние и односторонние повороты и ознакомившись с реорганизацией деревьев бинарного поиска за счет использования скошенных деревьев, пора приступить к исследованию соответствующего алгоритма балансировки.

Что должен делать алгоритм балансировки? В идеале он должен обеспечивать, чтобы длина пути от любого из листьев до корневого узла была одинаковой с точностью до единицы. На практике удовлетворить это строгое требование несколько затруднительно (AVL-деревья соответствуют этому определению, и их алгоритм балансировки удовлетворяет данному правилу). Поэтому мы определим какой-то алгоритм, который обеспечивает удовлетворение "менее строгого" требования, но не до такой степени "менее строгого", чтобы мы вернулись к тому, с чего начали.

В 1978 году Гюиба (Guibas) и Седжвик (Sedgewick) изобрели концепцию красно-черного дерева, удовлетворяющего такому умеренно нестрогому требованию. Красно-черные деревья (RB-деревья) - это структуры данных, используемые для реализации карт преобразования данных в библиотеке стандартных шаблонов С++ (С++ Standard Template Library). Красно-черный алгоритм предоставляет быстрый и эффективный метод балансировки дерева бинарного поиска, требующий для каждого узла не слишком много дополнительного объема памяти для хранения информации, необходимой для балансировки (в действительности для этого достаточно единственного дополнительного разряда).

Так что же собой представляют красно-черные деревья? Прежде всего, это дерево бинарного поиска, обладающее обычным простым алгоритмом поиска. Однако в красно-черном дереве каждый узел содержит определенную дополнительную информацию: каждый из них помечается как находящийся в одном из двух состояний. Эти два состояния называются красным (red) и черным (black).

Понятно, что этот подход применяется не просто для раскрашивания узлов, и в действительности необходимо выполнить еще три правила:

1. Считается, что нулевые дочерние связи на периферии дерева указывают на другие узлы (естественно, несуществующие). Эти невидимые нулевые узлы называются внешними узлами и всегда окрашены в черный цвет.

2. Условие для черных узлов: все пути от корневого узла до каждого из внешних узлов содержат одинаковое количество черных узлов.

3. Условие для красных узлов: каждый красный узел, не являющийся корневым, имеет черный родительский узел.

Учитывая, что до сих пор при создании деревьев мы вполне спокойно игнорировали эти нулевые связи, правило 1 кажется несколько усложненным. Тем не менее, его выполнение требуется, чтобы легче было выполнить правило 2. Следовательно, дерево с единственным узлом содержит также два внешних узла, являющиеся двумя нулевыми связями, исходящими из единственного реального узла (который называется внутренним). Второе правило - правило балансировки. Оно пытается поддерживать примерно одинаковую длину всех путей от корневого узла до каждого из внешних узлов. Эти пути будут различаться только количеством расположенных вдоль них красных узлов.

Набор простых красно-черных деревьев показан на рис. 8.6, при этом красные узлы изображены серыми квадратами (возможности одноцветной печати довольно-таки ограничены!), а внешние узлы - маленькими черными квадратами. Первое дерево (рисунок а) представляет пустое дерево - оно состоит всего из одного внешнего узла, который является черным - и, следовательно, по определению является красно-черным деревом. На примере второго и третьего деревьев (b и c) видно, что независимо от окрашивания корневого узла в красный или черный цвет, мы получаем красно-черное дерево. Эти деревья явно удовлетворяют всем трем правилам.

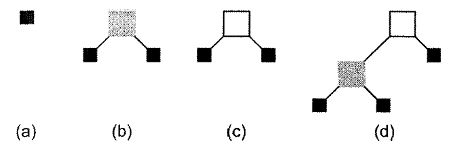
Рисунок 8.6. Набор простых красно-черных деревьев

Прежде чем продолжить, попытайтесь построить красно-черное дерево, содержащее два узла, корневой и левый дочерний, и три внешних узла (d). Выяснится, что в любом случае корневой узел должен быть окрашен в черный цвет, а его левый дочерний узел - в красный. Только такое окрашивание узлов позволяет удовлетворить все три правила.

Взглянем на это под другим углом. Посмотрите на рис. 8.7. Внутренние узлы этого дерева еще не окрашены. Можно ли их окрасить так, чтобы дерево удовлетворяло правилам 2 и 3? Никакого реального решения не существует. Невозможно окрасить внутренние узлы так, чтобы одновременно удовлетворить условия и для черных, и для красных узлов. Дерево, изображенное на рис. 8.7, не может быть красно-черным ни при каких условиях - и это хорошо, поскольку оно представляет начальную стадию вырождения дерева. Итак, важно усвоить следующий принцип: не все деревья могут быть окрашены в красный и черный цвета.

Фактически можно показать, что высота красно-черного дерева, содержащего n внутренних узлов, пропорциональна log n. Иначе говоря, в самом худшем случае для поиска в красно-черном дереве потребуется время, которое пропорционально O(log(n)). Именно к этому мы стремимся при использовании дерева бинарного поиска. Деревья, время поиска в которых пропорционально O(n), являются вырожденными.

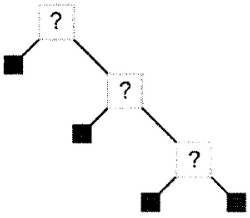
Рисунок 8.7. Дерево, которое не может быть окрашено в красный и черный цвета

Оглавление книги