Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Что такое энтропия?
Что такое энтропия?
Каково же точное определение энтропии физической системы? Мы уже знаем, что это некая мера явного беспорядка — но что означают такие не очень строгие понятия, как «явный» и «беспорядок»? Может возникнуть мысль, что энтропия — это величина, вообще не имеющая четкого физического определения. Кроме того, имеется еще одно обстоятельство, связанное со вторым началом термодинамики, которое еще в большей степени усиливает ощущение нестрогости обсуждаемого понятия: энтропия не остается постоянной и возрастает только в так называемых необратимых системах. Но что значит «необратимых»? На микроскопическом уровне, когда мы принимаем в расчет движения всех частиц, все системы оказываются обратимыми! Обычно мы полагаем, что падение стакана со стола и его разбивание, разбалтывание яйца или растворение сахара в кофе — суть процессы необратимые; в то же время, столкновения друг с другом небольшого числа частиц — процесс обратимый, так же, впрочем, как и вообще любой процесс, в котором путем некоторых ухищрений нам удается избежать превращения кинетической энергии в тепло. Термин «необратимый» служит нам, главным образом, лишь для указания на то, что проследить за микроскопическими движениями отдельных частиц или управлять ими было невозможно. Собственно, эти неконтролируемые движения и есть «тепло». Таким образом, может создаться впечатление, будто бы понятие «необратимости» обязано своим происхождением чисто «практическим» соображениям. Мы, конечно, и в самом деле не можем на практике отделить белок от желтка в разболтанном яйце, хотя подобная процедура и не противоречит законам механики. Поэтому возникает вопрос: а не будет ли все-таки наше определение энтропии зависеть от того, какие процессы практически осуществимы, а какие — нет?
Как уже говорилось в главе 5, физическое понятие энергии, так же как и импульса, и углового момента, имеют вполне четкие математические определения в терминах положений частиц, их скоростей, масс и действующих на них сил. А можем ли мы сходным образом определить понятие «явного беспорядка», которое, в свою очередь, необходимо для придания точного математического смысла понятию энтропии? Очевидно, что «явное» для одного наблюдателя может не быть таковым для другого. И вообще, не находится ли это «явное» в прямой зависимости от точности, с которой тот или иной наблюдатель способен изучать данную систему? Наблюдатель, располагающий более точной измерительной аппаратурой, способен получить намного больше информации о микроскопическом строении системы, чем другой наблюдатель, использующий менее совершенное оборудование. В этом случае один наблюдатель сможет обнаружить больше «скрытого порядка», чем другой, и он, разумеется, зафиксирует более низкий уровень энтропии данной системы, чем его коллега. Может даже сложиться впечатление, что и личные эстетические вкусы каждого из наблюдателей способны оказать решающее влияние на их выбор между «порядком» или «беспорядком». Предположим, что мы пригласили некоего художника, для которого россыпь осколков стекла на полу окажется настоящим произведением «искусства упорядочивания» по сравнению с безобразным, отвратительным стаканом, банально покоящимся на краю стола! Понизится ли и в самом деле энтропия системы после ее оценки наблюдателем с таким тонким артистическим восприятием?
Несмотря на все проблемы, связанные с субъективностью некоторых наших суждений, понятие энтропии оказывается замечательным образом применимо всякий раз, когда речь идет о точном научном описании — каковым и является само понятие энтропии! Причина этого заключается в том, что изменения, вызванные переходами системы от порядка к беспорядку, если их выразить в терминах микроскопических положений и скоростей частиц, поистине колоссальны и (почти во всех случаях) превосходят любые заметные на глаз отличия точек зрения на то, что считать «явным порядком» на макроскопическом уровне, а что — нет. В частности, любое заключение художника или ученого, относительно того, какой из стаканов обладает большим порядком — целый или разбитый, практически не имеет никакого отношения к их реальной энтропии. Намного больший вклад в энтропию дает случайное движение частиц, вызывающее незначительное нагревание стакана и воды, и растекание воды после удара стакана с водою о пол.
Теперь, чтобы точно сформулировать понятие энтропии, вернемся к идее фазового пространства, введенного в главе 5. Напомним, что фазовое пространство системы имеет, как правило, гигантское число измерений, а каждая его точка изображает с максимальной детализацией мгновенную конфигурацию системы. Подчеркнем, что «одна-единственная» точка фазового пространства определяет одновременно положения и импульсы всех отдельных частиц, составляющих рассматриваемую физическую систему. Все, что нам необходимо сейчас для определения энтропии, это сгруппировать вместе все те микроскопические состояния, которые выглядят совершенно одинаковыми с точки зрения их явных (т. е. макроскопических) свойств. Другими словами, нам необходимо разбить наше фазовое пространство на области (рис. 7.3),

Рис. 7.3. Гранулирование фазового пространства на области, соответствующие макроскопически неотличимым состояниям. Энтропия пропорциональна логарифму фазового объема
в каждой из которых различные точки изображают физические системы, отличающиеся на микроскопическом уровне расположением и скоростями частиц, но которые при этом совершенно неразличимы с точки зрения макроскопического наблюдателя, для которого все точки любой такой конкретной области будут описывать одну и ту же физическую систему. Подобное разбиение фазового пространства на области называется гранулированием фазового пространства.
После такого группирования некоторые из областей могут приобрести подавляюще огромные размеры по сравнению с другими областями. Рассмотрим, к примеру, фазовое пространство газа, заключенного в ящике. Наибольшая область фазового пространства будет приходиться на состояния, в которых частицы газа практически равномерно распределены по ящику с некоторым характерным распределением скоростей, обеспечивающим однородные давление и температуру. Это характерное распределение, в некотором смысле наиболее случайное из всех возможных, называется распределением Максвелла — по имени Джеймса Клерка Максвелла, которого мы уже упоминали ранее. В этом случае про газ говорят, что он находится в состоянии теплового равновесия. Подавляющая часть точек всего фазового пространства соответствует этому тепловому равновесию, и эти точки изображают всевозможные микроскопические значения координат и скоростей отдельных частиц, которые совместимы с состоянием теплового равновесия. Эта огромная часть является, конечно, только одной из многих областей нашего фазового пространства — но она оказывается (существенно) большей всех других областей, занимая практически все фазовое пространство! Рассмотрим теперь другое возможное состояние этого газа, скажем, такое, в котором весь газ собран в одном из углов ящика. В этом случае мы будем опять иметь целое множество различных микроскопических состояний, каждое из которых описывает газ сосредоточенным в углу ящика. Все эти состояния макроскопически неразличимы, и изображающие их точки фазового пространства заполняют в нем свою область. Однако объем этой области оказывается намного меньшим объема области для состояний теплового равновесия — примерно в
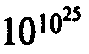
раз (если ящик — это метровый куб, содержащий воздух при нормальных условиях, а область в углу — сантиметровый кубик)!
Чтобы оценить различия в фазовых объемах, рассмотрим упрощенную ситуацию, в которой некоторое количество шаров распределено по большому числу ячеек. Предположим, что каждая ячейка может либо быть пустой, либо содержать один шар. Шары будут моделировать молекулы газа, а ячейки — различные положения молекул в ящике. Выделим небольшое подмножество ячеек, которое будем называть особым; оно будет соответствовать положению молекул газа в углу ящика. Для определенности условимся, что ровно 1/10 часть всех ячеек особая — т. е. в случае, когда имеется n особых ячеек, не особых будет ровно 9n (рис. 7.4).
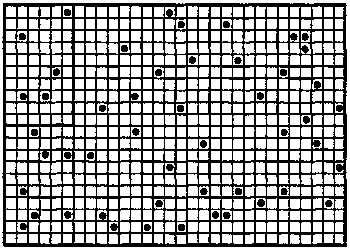
Рис. 7.4. Модель газа в ящике: некоторое количество шаров распределено по значительно большему числу ячеек. Одна десятая часть ячеек отмечены как особые. Эти ячейки выделены в левом верхнем углу
Мы хотим теперь случайным образом распределить m шаров среди всех ячеек и найти вероятность того, что все шары окажутся в особых ячейках. В случае, когда имеется только один шар и десять ячеек (т. е. имеется только одна особая ячейка), эта вероятность, очевидно, равна одной десятой. Тот же результат получится в случае одного шара и любого числа 10n ячеек (т. е. в случае n особых ячеек). Таким образом, для газа, состоящего только из одного атома, особая область, соответствующая «газу, собранному в углу ящика», будет иметь фазовый объем, составляющий лишь одну десятую всего объема «фазового пространства». Однако, если мы увеличим число шаров, вероятность того, что все они соберутся в особых ячейках, существенно понизится. Скажем, для двух шаров с двадцатью ячейками (две из которых особые) (m = 2, n = 2)[170], вероятность равна 1/190; в случае ста ячеек (среди них — десять особых) (m = 2, n = 10) вероятность равна 1/110; а при неограниченном увеличении числа ячеек с сохранением доли особых вероятность будет стремиться к 1/100.
Таким образом, в случае газа из двух атомов фазовый объем особой области составляет только одну сотую часть всего «фазового пространства». Для трех шаров и тридцати ячеек (m = 3, n = 3), он будет составлять 1/4060 всего фазового объема, а в пределе бесконечного числа ячеек — 1/1000 — т. е. для газа из трех атомов объем особой части будет составлять одну тысячную объема всего «фазового пространства». Для четырех шаров в пределе бесконечного числа ячеек вероятность становится равной 1/10000. Для пяти шаров — 1/100 000 и т. д. Для m шаров в пределе бесконечного числа ячеек вероятность стремится к 1/10m; т. е. для «газа» из m атомов фазовый объем особой области составляет только 1/10m от всего «фазового объема». (Этот результат остается справедливым, если учесть также и импульсы.)
Мы можем применить теперь те же оценки к нашей ситуации с реальным газом в ящике, только в этом случае для особой области нам нужно вместо одной десятой взять одну миллионную (1/1000000) от общего объема ящика (т. е. отношение объемов одного кубического сантиметра и одного кубического метра). В результате, вместо значения 1/10m для вероятности обнаружить все частицы газа в особой области, мы получим 1/1 000000m, т. е. 1/106m. Для воздуха, взятого при нормальных условиях, в нашем ящике находилось бы около 1025 молекул, поэтому мы принимаем m = 1025. Таким образом, особая область фазового пространства, представляющая состояния, в которых весь газ сосредоточен в углу ящика, составляет только
1/1060 000 000 000 000 000 000 000 000
часть всего фазового пространства!
Энтропия состояния — это мера объема V области фазового пространства, которая содержит все точки, представляющие данное состояние. Ввиду гигантской разницы между объемами, которую мы оценили выше, более удобным оказывается определять энтропию как величину, пропорциональную не самим объемам, а их логарифмам:
энтропия = k log V.
Использование логарифма делает все возникающие в расчетах числа более обозримыми. Так, к примеру, логарифм[171] 10000000 составляет всего-навсего число, близкое к 16. Величина k — константа, называемая постоянной Больцмана. Ее значение приблизительно равно 10-23 джоулей на один градус Кельвина.
Одним из важнейших следствий использования логарифма в определении энтропии является ее аддитивность в случае независимых систем. Другими словами, полная энтропия двух независимых физических систем, рассматриваемых как одна система, равна сумме их энтропий. (Это и есть основное свойство логарифмической функции: log АВ = log А + log В. Если эти подсистемы находятся в состояниях, изображающихся областями с объемами А и В в соответствующих им фазовых пространствах, то объем фазового пространства для составной системы будет равен произведению их объемов АВ, поскольку каждое микроскопическое состояние одной системы должно быть независимо учтено вместе с каждым микроскопическим состоянием другой; и, следовательно, энтропия составной системы, очевидно, будет равна именно сумме энтропий отдельных систем.)
Те гигантские отличия между размерами различных частей фазового пространства, о которых говорилось выше, в терминах энтропии будут выглядеть более скромно. Энтропия нашего кубического метра газа, как следует из предыдущих рассмотрений, оказывается всего на 1400 Дж/К (= 14k х 1025) больше энтропии того же газа, сосредоточенного в кубическом сантиметре «особой» области (так как
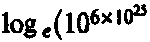
составляет примерно 14 х 1025).
Для того, чтобы определить реальные значения энтропии для указанных областей фазового пространства, нам осталось бы только немного позаботиться о выборе системы единиц (метры, джоули, килограммы, градусы Кельвина и т. д.). Однако, на самом деле, здесь было бы совсем неуместным заботиться об этом: для тех чудовищно огромных значений энтропии, которые я буду рассматривать в дальнейшем, выбор системы единиц не играет особой роли. Все же для определенности (и для специалистов), я скажу, что буду пользоваться так называемой естественной системой единиц, которая следует из законов квантовой механики и в которой постоянная Больцмана оказывается равной единице:
k = 1.
- Течение времени
- Неумолимое возрастание энтропии
- Что такое энтропия?
- Второе начало в действии
- Источник низкой энтропии во Вселенной
- Космология и Большой взрыв
- Горячий протошар
- Объясняется ли второе начало Большим взрывом?
- Черные дыры
- Структура пространственно-временны?х сингулярностей
- Насколько особым был Большой взрыв?
- 2 Энтропия в программах
- 1.1.1. Что такое объект
- Что делать
- Что делать, если при установке принтера появляется сообщение Невозможно завершение операции. Подсистема печати недоступн...
- Что дает грамотная должностная инструкция
- Как сделать, чтобы компьютер выключался
- ПОМОГАЙТЕ ДРУГИМ ПРИДЕРЖИВАТЬСЯ ПОЧТОВОГО «ЭТИКЕТА»
- Предисловие Кое-что новенькое – поговорим напрямую
- На что обращать внимание
- Что такое продажа?
- 1.5. Потренируйте свою интуицию: что следует запомнить
- Что происходит, когда бренды растут или идут на спад




