Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Структура пространственно-временны?х сингулярностей
Структура пространственно-временны?х
сингулярностей
Вспомним из главы 5 «Общая теория относительности Эйнштейна», как кривизна пространства-времени проявляется в приливных эффектах. Сферическая поверхность, образованная свободно падающими в гравитационном поле частицами некоторого большого тела, будет вытянута в одном направлении (вдоль линии, направленной на притягивающее тело) и сплюснута в перпендикулярном направлении. По мере приближения к притягивающему телу приливная деформация возрастает (рис. 7.15) по закону обратного куба расстояния до него.
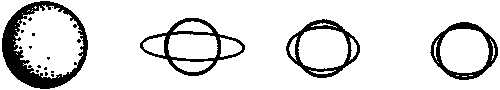
Рис. 7.15. Приливное воздействие, оказываемое сферическим притягивающим телом, возрастает по мере того, как другое тело приближается к нему, по закону обратного куба расстояния между центрами тел
Нарастающее приливное воздействие подобного рода будет ощущаться и астронавтом В по мере его падения на черную дыру и последующего движения внутри нее. Черные дыры с массой, равной нескольким солнечным, оказывали бы столь большое приливное воздействие, что космонавт не выдержал бы даже незначительного приближения к горизонту, не говоря уже о его пересечении. Для больших дыр величина приливного воздействия на горизонте может оказаться существенно меньше. Для черных дыр с массой в миллион солнечных, одна из которых, как предполагают астрономы, находится в центре нашей Галактики — Млечного Пути, — приливное воздействие на горизонте, испытываемое астронавтом, было бы ничтожно малым, так что он, в худшем случае, ощутил бы лишь небольшой дискомфорт. Однако, это приливное воздействие менялось бы по мере дальнейшего падения астронавта внутри дыры, так что за какие-то секунды оно достигло бы, в конце концов, бесконечной величины! И не только тело бедного астронавта оказалось бы разорванным на кусочки этой очень быстро возрастающей приливной силой, но, как в ускоренном кино, оказались бы разорванными и молекулы, из которых это тело состоит, потом составляющие эти молекулы атомы, их ядра, и, в конце концов, вообще все какие только есть субатомные частицы! Таким образом, «коллапс» разрушает все до основания.
При этом разрушается не только материя, но даже и само пространство-время прекращает свое существование. Такая окончательная катастрофа называется пространственно-временно?й сингулярностью. Читатель, конечно, может задаться справедливым вопросом, откуда мы знаем, что подобные катастрофы должны иметь место, и при каких обстоятельствах материю и пространство-время ожидает такая судьба. Вывод о неизбежности пространственно-временно?й сингулярности следует из классических уравнений общей теории относительности и оказывается справедливым при любых условиях, в которых находится уже сформировавшаяся черная дыра. Первоначальная модель Оппенгеймера и Снайдера (Оппенгеймер, Снайдер [1939]) как раз и демонстрировала поведение подобного типа. Долгое время, однако, астрофизики питали надежду, что такое сингулярное поведение является артефактом специальной симметрии, которая допускалась в этой модели с самого начала. Предполагалось, что в реалистичном (асимметричном) случае коллапсирующая материя могла бы скручиваться каким-то другим способом, а затем снова вырываться наружу. Но эти надежды исчезли после того, как было проведено математическое исследование более общего характера, которое послужило основой для формулировки так называемых теорем о сингулярности (см. Пенроуз [1965]; Хокинг, Пенроуз [1970]). Эти теоремы утверждали, что в рамках классической общей теории относительности с разумными источниками гравитации, пространственно-временны?е сингулярности неизбежны в случае гравитационного коллапса.
Таким же образом, меняя направление времени, мы приходим к выводу о неизбежности соответствующей начальной пространственно-временно?й сингулярности, которую мы теперь представляем как Большой взрыв, в любой (надлежащим образом) расширяющейся вселенной. Только теперь, вместо окончательного разрушения пространства-времени и материи, эта сингулярность представляет собой рождение пространства-времени и материи. Может показаться, что имеется полная временна?я симметрия между этими двумя типами сингулярностей: начальным типом, при котором пространство-время и материя рождаются, и конечным типом, когда пространство-время и материя уничтожаются. Конечно, между этими двумя ситуациями действительно имеется важная аналогия, но исследуя их более детально, мы обнаружим, что они не являются точными копиями, обращенными во времени относительно друг друга. И для нас важно разобраться в тех различиях геометрического характера, которые имеются между ними, поскольку именно они оказываются ключевыми в понимании источника второго начала термодинамики!
Обратимся к наблюдениям нашего астронавта В, который отважился на самопожертвование ради науки. Он наблюдает приливные силы, которые очень быстро возрастают до бесконечности. Поскольку он путешествует в пустом пространстве, то он ощущает деформирующие эффекты, которые оставляют величины объемов неизменными и которые создаются частью тензора пространственно-временно?й кривизны, обозначенной мною как ВЕЙЛЬ (см. главу 5, «Общая теория относительности Эйнштейна»). Другая часть тензора пространственно-временно?й кривизны, отвечающая за общее изменение объемов и называемая РИЧЧИ, обращается в нуль в пустом пространстве. Может оказаться, что В все же встретится с какой-нибудь материей в некоторый момент, но даже если это действительно произойдет (ведь, в конце концов, и сам астронавт состоит из материальных частиц), мы, вообще говоря, все равно обнаружим, что величина ВЕЙЛЬ будет намного превосходить величину РИЧЧИ. Таким образом, значение кривизны вблизи конечной сингулярности полностью определяется поведением тензора ВЕЙЛЬ. Этот тензор, вообще говоря, стремится к бесконечности:
ВЕЙЛЬ ? ?
(хотя это стремление может иметь осциллирующий характер). Эта ситуация оказывается типичной для пространственно-временной сингулярности[185]. Такое поведение связано с высокоэнтропийной сингулярностью.
Однако в случае Большого взрыва, ситуация оказывается совершенно другой. Стандартная модель Большого взрыва выводится из рассмотренных нами ранее вселенных Фридмана-Робертсона-Уокера, обладающих высокой степенью симметрии. Здесь деформирующее приливное воздействие, связанное с тензором ВЕЙЛЬ, вообще отсутствует. Вместо него теперь имеется направленное внутрь симметричное ускорение, действующее на любую сферическую поверхность, состоящую из пробных частиц (см. рис. 5.26). Но это — результат воздействия тензора РИЧЧИ, а не тензора ВЕЙЛЬ. В любой ФРУ-модели всегда имеет место тензорное уравнение:
ВЕЙЛЬ = 0.
По мере того, как мы приближаемся к начальной сингулярности все ближе и ближе, мы обнаруживаем, что именно РИЧЧИ, а не ВЕЙЛЬ, становится бесконечным и, таким образом, именно РИЧЧИ, а не ВЕЙЛЬ, определяет начальную сингулярность. Значит, мы имеем дело с низкоэнтропийной сингулярностью.
Если мы исследуем сингулярность схлопывания в точной коллапсирующей ФРУ-модели, мы и здесь обнаружим, что в момент схлопывания ВЕЙЛЬ = 0, тогда как РИЧЧИ стремится к бесконечности. Однако, эта особая ситуация дает нам совсем не то, что мы ожидаем от более реалистичной модели, в которой учитывается также и гравитационная конденсация. С течением времени вещество, находящееся первоначально в виде рассеянного газа, будет конденсироваться в звездные галактики. В этом процессе большое число звезд испытают гравитационное сжатие и превратятся в белые карлики, нейтронные звезды и черные дыры, а также в гигантские черные дыры, которые вполне могут образоваться в центрах галактик. Такого рода конденсация — особенно в случае черных дыр — связана с огромным возрастанием энтропии (рис. 7.16).
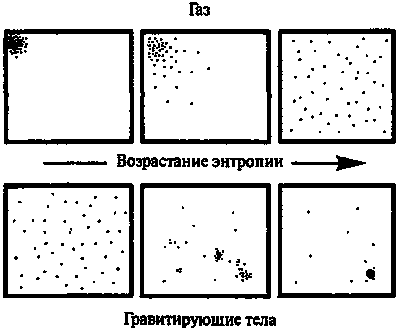
Рис. 7.16. Для обычного газа повышение энтропии связано с увеличением степени однородности его распределения внутри ящика. Для гравитирующих систем имеет место обратная ситуация. Высокая энтропия соответствует гравитационному конденсату, а максимальная — образованию черной дыры
Может показаться странным, на первый взгляд, что конденсированные состояния дают большую энтропию, чем состояния с однородным распределением, особенно если вспомнить, что для газа в ящике его конденсированные состояния (например, случай, когда весь газ собирается в одном из углов ящика) имели низкую энтропию, в то время как однородное распределение, соответствующее тепловому равновесию — имело высокую энтропию. При учете гравитации ситуация меняется на обратную благодаря универсальности гравитационного притяжения. С течением времени, конденсация становится все более и более сильной и, в конце концов, множество сконденсировавшихся черных дыр соединяет свои сингулярности в финальной сингулярности большого коллапса. Такая конечная сингулярность не имеет ничего общего с тем идеализированным большим коллапсом, который имеет место в коллапсирующей ФРУ-модели, где действовало ограничение ВЕЙЛЬ = 0. По мере накопления числа сконденсировавшихся объектов, тензор ВЕЙЛЬ имеет тенденцию непрерывно увеличиваться[186] и, вообще говоря, ВЕЙЛЬ ? ? в конечной сингулярности. Посмотрите на рис. 7.17, где показана полная история замкнутой вселенной в соответствии с этой общей картиной.

Рис, 7.17. Полная история замкнутой вселенной, которая начинается с однородного низкоэнтропийного большого взрыва с ограничением ВЕЙЛЬ = 0 и заканчивается высокоэнтропийным большим коллапсом — представляющим собой сгущение большого числа черных дыр — с условием ВЕЙЛЬ ? ?
Мы видим теперь, как становится возможной ситуация, когда сжимающаяся вселенная может не обладать низкой энтропией. Та «малость» энтропии Большого взрыва, которая обеспечивает нам выполнение второго начала, не была, таким образом, следствием одной только «малости» вселенной в момент взрыва! Если бы мы обратили во времени картину большого коллапса, к которой только что пришли, мы бы получили «большой взрыв» с чрезвычайно высокой энтропией, где не было бы второго начала! По некоторым причинам, вселенная возникла в особом (низкоэнтропийном) состоянии, на которое было наложено условие типа ВЕЙЛЬ = 0 для ФРУ-моделей. И если бы подобного рода ограничение не имело места, то «намного более вероятной» могла бы оказаться ситуация, в которой как начальная, так и конечная сингулярности были бы высокоэнтропийного типа ВЕЙЛЬ ? ? (рис. 7.18).

Рис. 7.18. Если убрать ограничение ВЕЙЛЬ = 0, то большой взрыв получится тоже высокоэнтропийным, с условием ВЕЙЛЬ ? ?. Такая вселенная была бы сплошь испещрена белыми дырами и в ней не выполнялось бы второе начало термодинамики — в полном противоречии с нашим опытом
В такой гипотетической вселенной, конечно же, не нашлось бы места для второго начала термодинамики!
- Течение времени
- Неумолимое возрастание энтропии
- Что такое энтропия?
- Второе начало в действии
- Источник низкой энтропии во Вселенной
- Космология и Большой взрыв
- Горячий протошар
- Объясняется ли второе начало Большим взрывом?
- Черные дыры
- Структура пространственно-временны?х сингулярностей
- Насколько особым был Большой взрыв?
- Структура пространственно-временны?х сингулярностей
- СТРУКТУРА ПРОСТОЙ ПРОГРАММЫ
- Физическая структура базы данных
- Логическая структура базы данных InterBase
- Эффективная работа с временными файлами сортировки
- Оптимальная структура хранения записей
- Одновременный запуск нескольких копий сервера (multi-instancing)
- 2.2. Современные методы исследования эффективности рекламы
- Безопасность временных таблиц
- Новая структура данных на диске: ODS11
- Структура UFS
- 2. Структура экспертных систем




