Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER EIGHT: Learning Without a Teacher

CHAPTER EIGHT: Learning Without a Teacher

If you’re a parent, the entire mystery of learning unfolds before your eyes in the first three years of your child’s life. A newborn baby can’t talk, walk, recognize objects, or even understand that a object continues to exist when the baby isn’t looking at it. But month after month, in steps large and small, by trial and error and great conceptual leaps, the child figures out how the world works, how people behave, and how to communicate. By a child’s third birthday, all this learning has coalesced into a stable self, a stream of consciousness that will continue throughout life. Older children and adults can time-travel, aka remember things past, but only so far back. If we could revisit ourselves as infants and toddlers and see the world again through those newborn eyes, much of what puzzles us about learning-even about existence itself-would suddenly seem obvious. But as it is, the greatest mystery in the universe is not how it begins or ends, or what infinitesimal threads it’s woven from, it’s what goes on in a small child’s mind: how a pound of gray jelly can grow into the seat of consciousness.

The scientific study of children’s learning is still young, having begun in earnest only a few decades ago, but it has already come remarkably far. Infants can’t answer questionnaires or follow experimental protocols, but we can infer a surprising amount about what goes on in their minds by videotaping and studying their reactions during experiments. A coherent picture emerges: an infant’s mind isn’t just the unfolding of a predefined genetic program or a biological device for recording correlations in sense data; rather, the infant’s mind actively synthesizes his or her reality, and this reality changes quite radically over time.

Increasingly, and most relevant to us, cognitive scientists express their theories of children’s learning in the form of algorithms. Many machine-learning researchers take inspiration from this. Everything we need is right there in a child’s mind, if only we can somehow capture its essence in computer code. Some researchers even argue that the way to create intelligent machines is to build a robot baby and let him experience the world as a human baby does. We, the researchers, would be his parents (perhaps even with an assist from crowdsourcing, giving a whole new meaning to the term global village). Little Robby-let’s call him that, in honor of the chubby but much taller robot in Forbidden Planet-is the only robot baby we’ll ever have to build. Once he has learned everything a three-year-old knows, the AI problem is solved. We can copy the contents of his mind into as many other robots as we like, and they’ll take it from there, the hardest part already accomplished.

The question, of course, is what algorithm should be running in Robby’s brain at birth. Researchers influenced by child psychology look askance at neural networks because the microscopic workings of a neuron seem a million miles from the sophistication of even a child’s most basic behaviors, like reaching for an object, grasping it, and inspecting it with wide, curious eyes. We need to model the child’s learning at a higher level of abstraction, lest we miss the planet for the trees. Above all, even though children certainly get plenty of help from their parents, they learn mostly on their own, without supervision, and that’s what seems most miraculous. None of the algorithms we’ve seen so far can do it, but we’re about to see several that can-bringing us one step closer to the Master Algorithm.

Putting together birds of a feather

We flip the “on” switch, and Robby’s video eyes open for the very first time. At once he’s flooded with what William James memorably called the “blooming, buzzing confusion” of the world. With new images streaming in at a rate of dozens per second, one of the first things he must do is learn to organize them into larger chunks. The real world is made up of objects that persist over time, not random pixels changing arbitrarily from one moment to the next. Mommy isn’t replaced by a smaller Mommy when she walks away. Putting a dish on the table doesn’t make a white hole in it. A young baby is not surprised if a teddy bear passes behind a screen and reemerges as an airplane, but a one-year-old is. Somehow, he’s figured out that teddy bears are different from airplanes and don’t spontaneously transmute. Soon afterward, he’ll figure out that some objects are more alike than others and start forming categories. Given a pile of toy horses and pencils to play with, a nine-month-old doesn’t think to sort them into separate piles of horses and pencils, but an eighteen-month-old does.

Organizing the world into objects and categories is second nature to an adult but not to an infant, and even less to Robby the robot. We could endow him with a visual cortex in the form of a multilayer perceptron and show him labeled examples of all the objects and categories in the world-here’s Mommy close up, here’s Mommy far away-but we’d never be done. What we need is an algorithm that will spontaneously group together similar objects, or different images of the same object. This is the problem of clustering, and it’s one of the most intensively studied in machine learning.

A cluster is a set of similar entities, or at a minimum, a set of entities that are more similar to each other than to members of other clusters. It’s human nature to cluster things, and it’s often the first step on the road to knowledge. When we look up at the night sky, we can’t help seeing clusters of stars, and then we fancifully name them after shapes they resemble. Noticing that certain sets of elements had very similar chemical properties was the first step in discovering the periodic table. Each of those sets is now a column in it. Everything we perceive is a cluster, from friends’ faces to speech sounds. Without them, we’d be lost: children can’t learn a language before they learn to identify the characteristic sounds it’s made of, which they do in their first year of life, and all the words they then learn mean nothing without the clusters of real things they refer to. Confronted with big data-a very large number of objects-our first recourse is to group them into a more manageable number of clusters. A whole market is too coarse, and individual customers are too fine, so marketers divide markets into segments, which is their word for clusters. Even objects themselves are at bottom clusters of their observations, from all the different angles light falls on Mommy’s face to all the different sound waves baby hears as the word mommy. And we can’t think without objects, which is perhaps why quantum mechanics is so unintuitive: we want to visualize the subatomic world as particles colliding, or waves interfering, but it’s not really either.

We can represent a cluster by its prototypical element: the image of your mother that you see with your mind’s eye or the quintessential cat, sports car, country house, or tropical beach. Peoria, Illinois, is the average American town, according to marketing lore. Bob Burns, a fifty-three-year-old building maintenance supervisor in Windham, Connecticut, is America’s most ordinary citizen-at least if you believe Kevin O’Keefe’s book The Average American. Anything described by numeric attributes-say, people’s heights, weights, girths, shoe sizes, hair lengths, and so on-makes it easy to compute the average member: his height is the average height of all the cluster members, his weight the average of all the weights, and so on. For categorical attributes, like gender, hair color, zip code, or favorite sport, the “average” is simply the most frequent value. The average member described by this set of attributes may or may not be a real person, but either way it’s a useful reference to have: if you’re brainstorming how to market a new product, picturing Peoria as the town where you’re launching it or Bob Burns as your target customer beats thinking of abstract entities like “the market” or “the consumer.”

As useful as such averages are, we can do even better; indeed the whole point of big data and machine learning is to avoid thinking at such a coarse level. Our clusters can be very specialized sets of people or even different aspects of the same person: Alice buying books for work, for leisure, or as Christmas presents; Alice in a good mood versus Alice with the blues. Amazon would like to distinguish the books Alice buys for herself from the ones she buys for her boyfriend, as this would allow it to make appropriate recommendations at appropriate times. Unfortunately, purchases don’t come labeled with “self-gift” or “for Bob,” and Amazon needs to figure out how to group them.

Suppose the entities in Robby’s world fall into five clusters (people, furniture, toys, food, and animals), but we don’t know which things belong to which clusters. This is the type of problem that Robby faces when we switch him on. One simple option for sorting entities into clusters is to pick five random objects as the cluster prototypes and then compare each entity with each prototype and assign it to the most similar prototype’s cluster. (As in analogical learning, the choice of similarity measure is important. If the attributes are numeric, it can be as simple as Euclidean distance, but there are many other options.) We now need to update the prototypes. After all, a cluster’s prototype is supposed to be the average of its members, and although that was necessarily the case when each cluster had only one member, it generally won’t be after we have added a bunch of new members to each cluster. So for each cluster, we compute the average properties of its members and make that the new prototype. At this point, we need to update the cluster memberships again: since the prototypes have moved, the closest prototype to a given entity may also have changed. Let’s imagine the prototype of one category was a teddy bear and the prototype of another was a banana. Perhaps on our first run we grouped an animal cracker with the bear, but on the second we grouped it with the banana. An animal cracker initially looked like a toy, but now it looks more like food. Once I reclassify animal crackers in the banana group, perhaps the prototypical item for that group also changes, from a banana to a cookie. This virtuous cycle, with entities assigned to better and better clusters, continues until the assignment of entities to clusters doesn’t change (and therefore neither do the cluster prototypes).

This algorithm is called k-means, and its origins go back to the fifties. It’s nice and simple and quite popular, but it has several shortcomings, some of which are easier to solve than others. For one, we need to fix the number of clusters in advance, but in the real world, Robby is always running into new kinds of objects. One option is to let an object start a new cluster if it’s too different from the existing ones. Another is to allow clusters to split and merge as we go along. Either way, we probably want the algorithm to include a preference for fewer clusters, lest we wind up with each object as its own cluster (hard to beat if we want clusters to consist of similar objects, but clearly not the goal).

A bigger issue is that k-means only works if the clusters are easy to tell apart: each cluster is roughly a spherical blob in hyperspace, the blobs are far from each other, and they all have similar volumes and include a similar number of objects. If any of these fails, ugly things can happen: an elongated cluster is split into two different ones, a smaller cluster is absorbed into a larger one nearby, and so on. Luckily, there’s a better option.

Suppose we decide that letting Robby roam around in the real world is too slow and cumbersome a way to learn. Instead, like a would-be pilot learning in a flight simulator, we’ll have him look at computer-generated images. We know what clusters the images come from, but we’re not telling Robby. Instead, we create each image by first choosing a cluster at random (toys, say) and then synthesizing an example of that cluster (small, fluffy, brown teddy bear with big black eyes, round ears, and a bow tie). We also choose the properties of the example at random: the size comes from a normal distribution with a mean of ten inches, the fur is brown with 80 percent probability and white otherwise, and so on. After Robby has seen lots of images generated in this way, he should have learned to cluster them into people, furniture, toys, and so on, because people are more like people than furniture and so on. But the interesting question is: If we look at it from Robby’s point of view, what’s the best algorithm to discover the clusters? The answer is surprising: Na?ve Bayes, which we first met as an algorithm for supervised learning. The difference is that now Robby doesn’t know the classes, so he’ll have to guess them!

Clearly, if Robby did know them, it would be smooth sailing: as in Na?ve Bayes, each cluster would be defined by its probability (17 percent of the objects generated were toys), and by the probability distribution of each attribute among the cluster’s members (for example, 80 percent of the toys are brown). Robby could estimate these probabilities just by counting the number of toys in the data, the number of brown toys, and so on. But in order to do that, we would need to know which objects are toys. This seems like a tough nut to crack, but it turns out we already know how to do it as well. If Robby has a Na?ve Bayes classifier and needs to figure out the class of a new object, all he needs to do is apply the classifier and compute the probability of each class given the object’s attributes. (Small, fluffy, brown, bear-like, with big eyes, and a bow tie? Probably a toy but possibly an animal.)

So Robby is faced with a chicken-and-egg problem: if he knew the objects’ classes, he could learn the classes’ models by counting, and if he knew the models, he could infer the objects’ classes. We seem to be stuck again, but far from it: just start by guessing a class for each object any way you want-even at random-and you’re off to the races. From those classes and the data, you can learn the class models; based on these models you can reinfer the classes and so on. At first sight this looks like a crazy scheme: it may never finish, circling forever between inferring the classes from the models and the models from the classes, and even if it does finish, there’s no reason to believe it will settle on meaningful clusters. But in 1977 a trio of Harvard statisticians (Arthur Dempster, Nan Laird, and Donald Rubin) showed that the crazy scheme actually works: every time we go around the loop, the cluster model gets better, and the loop ends when the model is a local maximum of the likelihood. They called this scheme the EM algorithm, where the E stands for expectation (inferring the expected probabilities) and the M for maximization (estimating the maximum-likelihood parameters). They also showed that many previous algorithms were special cases of EM. For example, to learn hidden Markov models, we alternate between inferring the hidden states and estimating the transition and observation probabilities based on them. Whenever we want to learn a statistical model but are missing some crucial information (e.g., the classes of the examples), we can use EM. This makes it one of the most popular algorithms in all of machine learning.

You might have noticed a certain resemblance between k-means and EM, in that they both alternate between assigning entities to clusters and updating the clusters’ descriptions. This is not an accident: k-means itself is a special case of EM, which you get when all the attributes have “narrow” normal distributions, that is, normal distributions with very small variance. When clusters overlap a lot, an entity could belong to, say, cluster A with a probability of 0.7 and cluster B with a probability of 0.3, and we can’t just decide that it belongs to cluster A without losing information. EM takes this into account by fractionally assigning the entity to the two clusters and updating their descriptions accordingly. If the distributions are very concentrated, however, the probability that an entity belongs to the nearest cluster is always approximately 1, and all we have to do is assign entities to clusters and average the entities in each cluster to obtain its mean, which is just the k-means algorithm.

So far we’ve only seen how to learn one level of clusters, but the world is, of course, much richer than that, with clusters within clusters all the way down to individual objects: living things cluster into plants and animals, animals into mammals, birds, fishes, and so on, all the way down to Fido the family dog. No problem: once we’ve learned one set of clusters, we can treat them as objects and cluster them in turn, and so on up to the cluster of all things. Alternatively, we can start with a coarse clustering and then further divide each cluster into subclusters: Robby’s toys divide into stuffed animals, constructions toys, and so on; stuffed animals into teddy bears, plush kittens, and so on. Children seem to start out in the middle and then work their way up and down. For example, they learn dog before they learn animal or beagle. This might be a good strategy for Robby, as well.

Discovering the shape of the data

Whether it’s data pouring into Robby’s brain through his senses or the click streams of millions of Amazon customers, grouping a large number of entities into a smaller number of clusters is only half the battle. The other half is shortening the description of each entity. The very first picture of Mom that Robby sees comprises perhaps a million pixels, each with its own color, but you hardly need a million variables to describe a face. Likewise, each thing you click on at Amazon provides an atom of information about you, but what Amazon would really like to know is your likes and dislikes, not your clicks. The former, which are fairly stable, are somehow immanent in the latter, which grow without limit as you use the site. Little by little, all those clicks should add up to a picture of your taste, in the same way that all those pixels add up to a picture of your face. The question is how to do the adding.

A face has only about fifty muscles, so fifty numbers should suffice to describe all possible expressions, with plenty of room to spare. The shape of the eyes, nose, mouth, and so on-the features that let you tell one person from another-shouldn’t take more than a few dozen numbers, either. After all, with only ten choices for each facial feature, a police artist can put together a sketch of a suspect that’s good enough to recognize him. You can add a few more numbers to specify lighting and pose, but that’s about it. So if you give me a hundred numbers or so, that should be enough to re-create a picture of a face. Conversely, Robby’s brain should be able to take in a picture of a face and quickly reduce it to the hundred numbers that really matter.

Machine learners call this process dimensionality reduction because it reduces a large number of visible dimensions (the pixels) to a few implicit ones (expression, facial features). Dimensionality reduction is essential for coping with big data-like the data coming in through your senses every second. A picture may be worth a thousand words, but it’s also a million times more costly to process and remember. Yet somehow your visual cortex does a pretty good job of whittling it down to a manageable amount of information, enough to navigate the world, recognize people and things, and remember what you saw. It’s one of the great miracles of cognition and so natural you’re not even conscious of doing it.

When you arrange books on a shelf so that books on similar topics are close to each other, you’re doing a kind of dimensionality reduction, from the vast space of topics to the one-dimensional shelf. Unavoidably, some books that are closely related will wind up far apart on the shelf, but you can still order them in a way that minimizes such occurrences. That’s what dimensionality reduction algorithms do.

Suppose I give you the GPS coordinates of all the shops in Palo Alto, California, and you plot a few of them on a piece of paper:

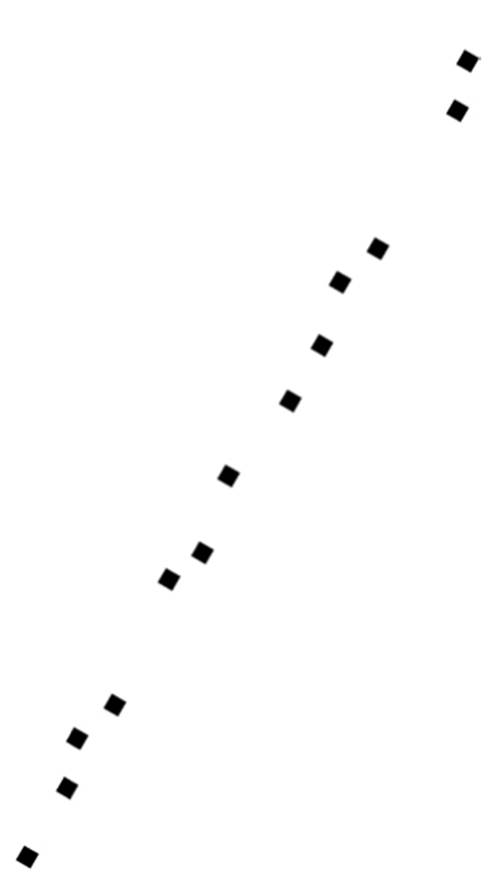
You can probably tell just by looking at this plot that the main street in Palo Alto runs southwest-northeast. You didn’t draw a street, but you can intuit that it’s there from the fact that all the points fall along a straight line (or close to it-they can be on different sides of the street). Indeed, the street is University Avenue, and if you want to shop or eat out in Palo Alto, that’s the place to go. As a bonus, once you know that the shops are on University Avenue, you don’t need two numbers to locate them, just one: the street number (or, if you wanted to be really precise, the distance from the shop to the Caltrain station, on the southwest corner, which is where University Avenue begins).

If you plot more shops, you’ll probably notice that some are on cross streets, a little bit off University Avenue, and a few are elsewhere entirely:

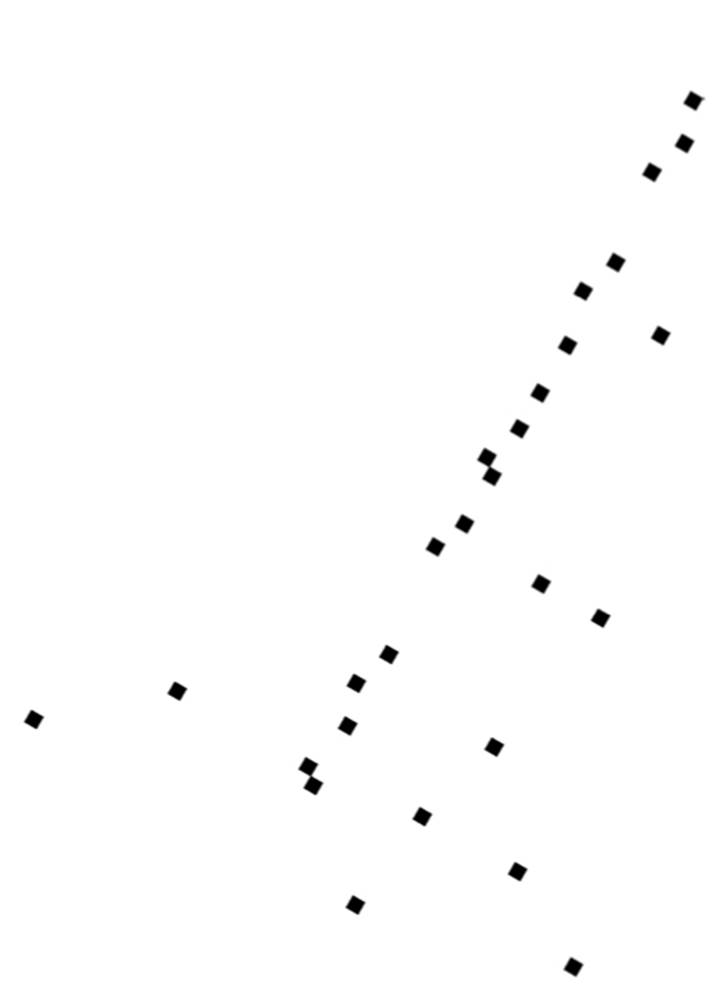
Nevertheless, it’s still the case that most shops are pretty close to University Avenue, and if you were allowed only one number to locate a shop, its distance from the Caltrain station along the avenue would be a pretty good choice: after walking that distance, looking around is probably enough to find the shop. So you’ve just reduced the dimensionality of “shop locations in Palo Alto” from two to one.

Robby doesn’t have the benefit of your highly evolved visual system, though, so if you want him to go fetch your dry cleaning from Elite Cleaners and you only allow his map of Palo Alto to have one coordinate, he needs an algorithm to “discover” University Avenue from the GPS coordinates of the shops. The key to this is to notice that, if you put the origin of the x,y plane at the average of the shops’ locations and slowly rotate the axes, the shops are closest to the x axis when you’ve turned it by about 60 degrees, that is, when it lines up with University Avenue:

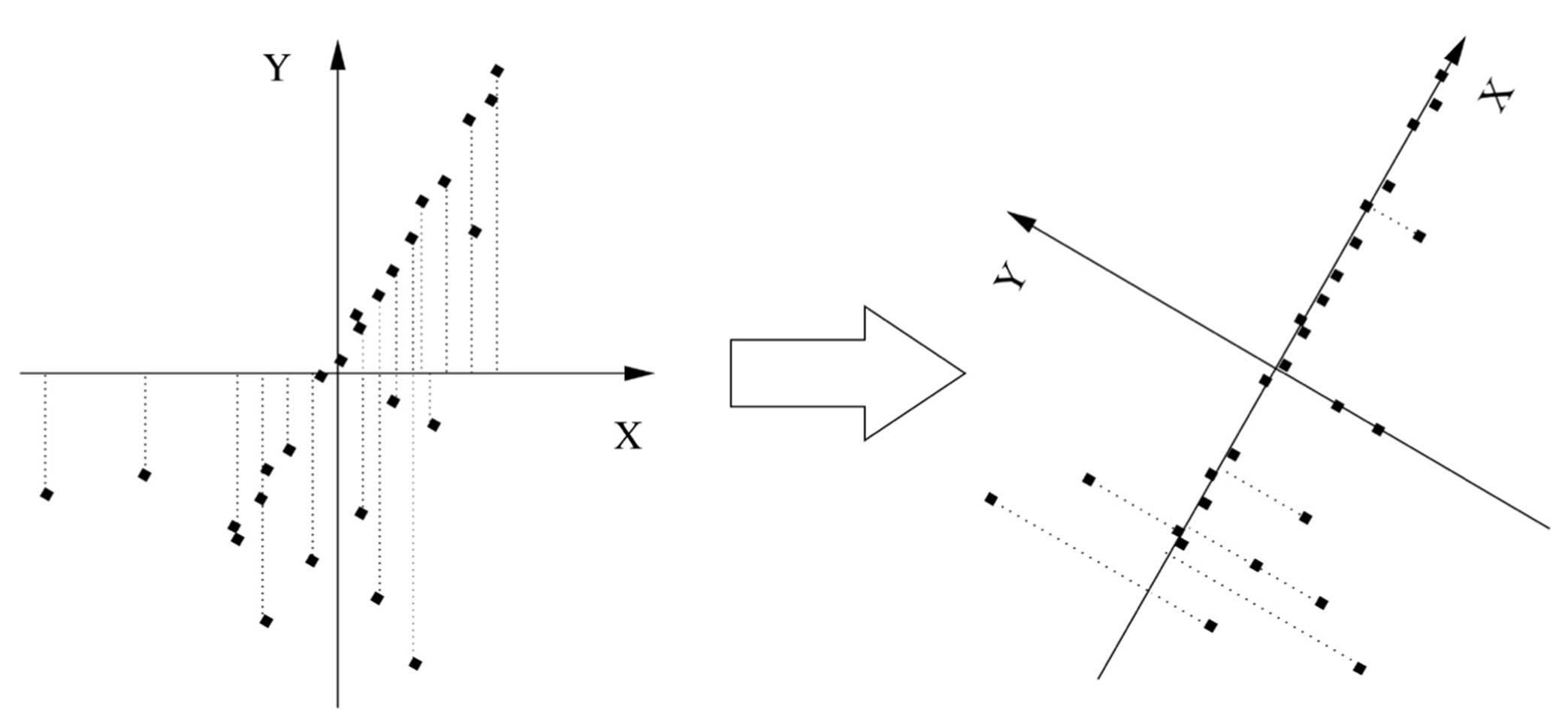
This direction-known as the first principal component of the data-is also the direction along which the spread of the data is greatest. (Notice how, if you project the shops onto the x axis, they’re farther apart in the right figure than in the left one.) After you’ve found the first principal component, you can look for the second one, which in this case is the direction of greatest variation at right angles to University Avenue. On a map, there’s only one possible direction left (the direction of the cross streets). But if Palo Alto was on a hillside, one or both of the two first principal components would be partly uphill, and the third and last one would be up into the air. We can apply the same idea to data in thousands or millions of dimensions, like face images, successively looking for the directions of greatest variation until the remaining variability is small, at which point we can stop. For example, after rotating the axes in the figure above, most shops have y = 0, so the average y is very small, and we don’t lose too much information by ignoring the y coordinate altogether. And if we decide to keep y, surely z (up into the air) is insignificant. As it turns out, the whole process of finding the principal components can all be accomplished in one shot with a bit of linear algebra. Best of all, a few dimensions often account for the bulk of the variation in even very high-dimensional data. Even if that’s not the case, eyeballing the data in the top two or three dimensions often yields a lot of insight because it takes advantage of your visual system’s amazing powers of perception.

Principal-component analysis (PCA), as this process is known, is one of the key tools in the scientist’s toolkit. You could say PCA is to unsupervised learning what linear regression is to the supervised variety. The famous hockey-stick curve of global warming, for example, is the result of finding the principal component of various temperature-related data series (tree rings, ice cores, etc.) and assuming it’s the temperature. Biologists use PCA to summarize the expression levels of thousands of different genes into a few pathways. Psychologists have found that personality boils down to five dimensions-extroversion, agreeableness, conscientiousness, neuroticism, and openness to experience-which they can infer from your tweets and blog posts. (Chimps supposedly have one more dimension-reactivity-but Twitter data for them is not available.) Applying PCA to congressional votes and poll data shows that, contrary to popular belief, politics is not mainly about liberals versus conservatives. Rather, people differ along two main dimensions: one for economic issues and one for social ones. Collapsing these into a single axis mixes together populists and libertarians, who are polar opposites, and creates the illusion of lots of moderates in the middle. Trying to appeal to them is an unlikely winning strategy. On the other hand, if liberals and libertarians overcame their mutual aversion, they could ally themselves on social issues, where both favor individual freedom.

When he grows up, Robby can use a variant of PCA to solve the “cocktail party” problem, which is to pick out individual voices from the babble of the crowd. A related method can help him learn to read. If each word is a dimension, then a text is a point in the space of words, and the main directions of that space turn out to be elements of meaning. For example, President Obama and the White House are far apart in word space but close together in meaning space, because they tend to appear in similar contexts. Believe it or not, this type of analysis is all it takes for computers to grade SAT essays as well as humans do. Netflix uses a similar idea. Instead of just recommending movies that users with similar tastes liked, it first projects both users and movies into a lower-dimensional “taste space” and recommends a movie if it’s close to you in this space. That way it can find movies for you that you never knew you’d love.

You’d probably be disappointed if you looked at the principal components of a face data set, though. They’re not what you’d expect, such as facial expressions or features, but more like ghostly faces, blurred beyond recognition. This is because PCA is a linear algorithm, and so all that the principal components can be is weighted pixel-by-pixel averages of real faces. (Also known as eigenfaces because they’re eigenvectors of the centered covariance matrix of the data-but I digress.) To really understand faces, and most shapes in the world, we need something else: nonlinear dimensionality reduction.

Suppose we zoom out from Palo Alto, and I give you the GPS coordinates of the main cities in the Bay Area:

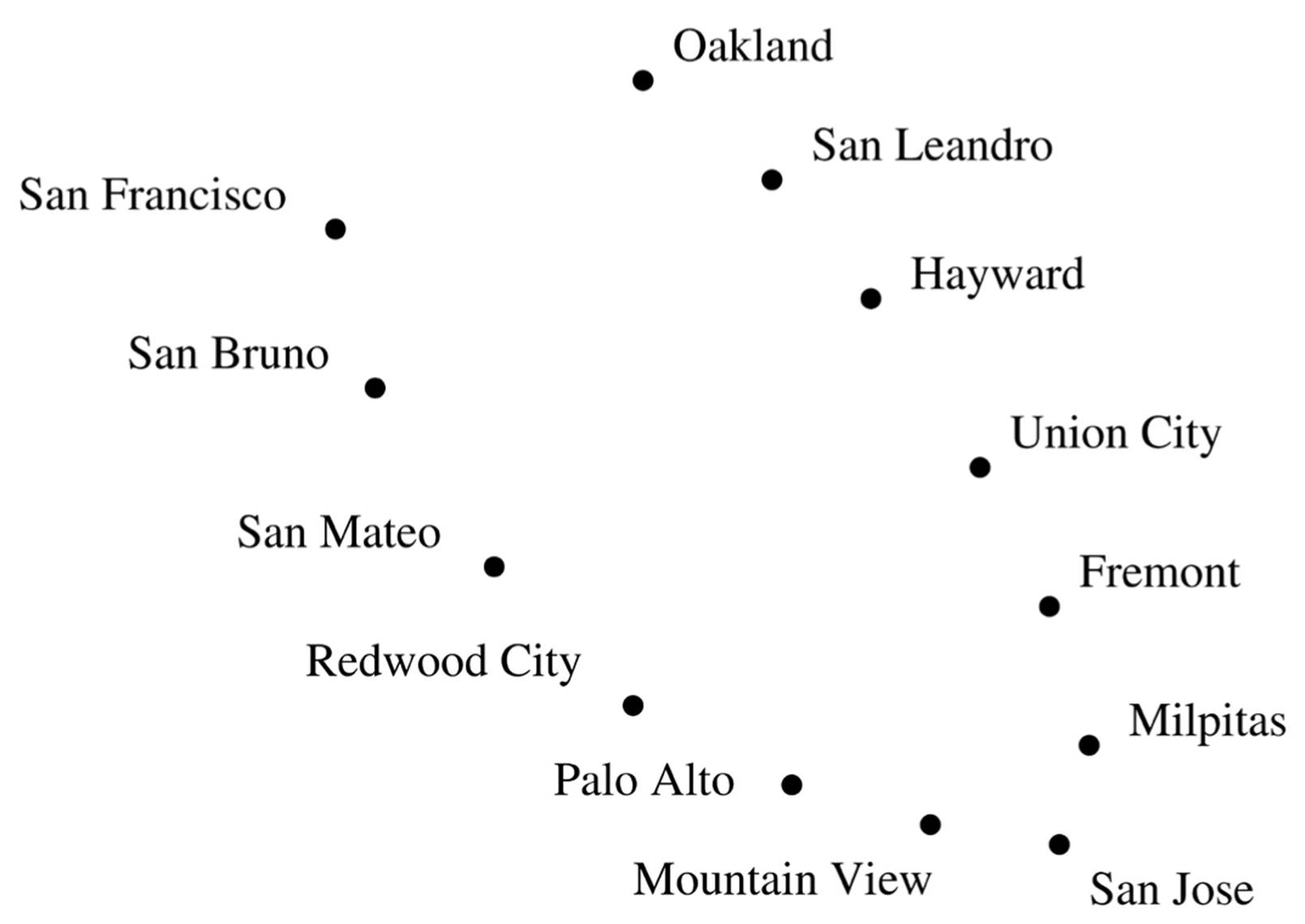
Again, you can probably surmise just by looking at this plot that the cities are on a bay, and if you draw a line running through them, you can locate each city using just one number: how far it is from San Francisco along that line. But PCA can’t find this curve; instead, it draws a straight line running down the middle of the bay, where there are no cities at all. Far from elucidating the shape of the data, PCA obscures it.

Instead, imagine for a moment that we’re going to develop the Bay Area from scratch. We’ve decided where each city will be located, and our budget allows us to build a single road connecting them. Naturally, we lay down a road that goes from San Francisco to San Bruno, from there to San Mateo, and so on all the way to Oakland. This road is a pretty good one-dimensional representation of the Bay Area and can be found by a simple algorithm: build a road between each pair of nearby cities. Of course, in general this will result in a network of roads, not a single road running by every city. But we can force the latter by building the single road that best approximates the network, in the sense that the distances between cities along this road are as close as possible to the distances along the network.

One of the most popular algorithms for nonlinear dimensionality reduction, called Isomap, does just this. It connects each data point in a high-dimensional space (a face, say) to all nearby points (very similar faces), computes the shortest distances between all pairs of points along the resulting network and finds the reduced coordinates that best approximate these distances. In contrast to PCA, faces’ coordinates in this space are often quite meaningful: one may represent which direction the face is facing (left profile, three quarters, head on, etc.); another how the face looks (very sad, a little sad, neutral, happy, very happy, etc.); and so on. From understanding motion in video to detecting emotion in speech, Isomap has a surprising ability to zero in on the most important dimensions of complex data.

Here’s an interesting experiment. Take the video stream from Robby’s eyes, treat each frame as a point in the space of images, and reduce that set of images to a single dimension. What will you discover? Time. Like a librarian arranging books on a shelf, time places each image next to its most similar ones. Perhaps our perception of it is just a natural result of our brains’ dimensionality reduction prowess. In the road network of memory, time is the main thoroughfare, and we soon find it. Time, in other words, is the principal component of memory.

The hedonistic robot

Clustering and dimensionality reduction get us closer to human learning, but there’s still something very important missing. Children don’t just passively observe the world; they do things. They pick up objects they see, play with them, run around, eat, cry, and ask questions. Even the most advanced visual system is of no use to Robby if it doesn’t help him interact with the environment. Robby needs to know not just what’s where but what to do at each moment. In principle we could teach him using step-by-step instructions, pairing sensor readings with the appropriate actions to take in response, but this is viable only for narrow tasks. The actions you take depend on your goals, not just whatever you are currently perceiving, and those goals can be far in the future. Step-by-step supervision shouldn’t be needed, in any case. Parents don’t teach their children to crawl, walk, or run; they figure it out on their own. But none of the learning algorithms we’ve seen so far can do this.

Humans do have one constant guide: their emotions. We seek pleasure and avoid pain. When you touch a hot stove, you instinctively recoil. That’s the easy part. The hard part is learning not to touch the stove in the first place. That requires moving to avoid a sharp pain that you have not yet felt. Your brain does this by associating the pain not just with the moment you touch the stove, but with the actions leading up to it. Edward Thorndike called this the law of effect: actions that lead to pleasure are more likely to be repeated in the future; actions that lead to pain, less so. Pleasure travels back through time, so to speak, and actions can eventually become associated with effects that are quite remote from them. Humans can do this kind of long-range reward seeking better than any other animal, and it’s crucial to our success. In a famous experiment, children were presented with a marshmallow and told that if they resisted eating it for a few minutes, they could have two. The ones who succeeded went on to do better in school and adult life. Perhaps less obviously, companies using machine learning to improve their websites or their business practices face a similar problem. A company may make a change that brings in more revenue in the short term-like selling an inferior product that costs less to make for the same price as the original superior product-but miss seeing that doing this will lose customers in the longer term.

The learners we saw in the previous chapters are all guided by instant gratification: every action, whether it’s flagging a spam e-mail or buying a stock, gets an immediate reward or punishment from the teacher. But there’s a whole subfield of machine learning dedicated to algorithms that explore on their own, flail, hit on rewards, and figure out how to get them again in the future, much like babies crawling around and putting things in their mouths.

It’s called reinforcement learning, and your first housebot will probably use it a lot. If you ask Robby to make eggs and bacon for you right after you’ve unpacked him and turned him on, it may take a while. But then, while you’re at work, he will explore the kitchen, noting where various things are and what kind of stove you have. By the time you get back, dinner will be ready.

An important precursor of reinforcement learning was a checkers-playing program created by Arthur Samuel, an IBM researcher, in the 1950s. Board games are a great example of a reinforcement learning problem: you have to make a long series of moves without any feedback, and the whole reward or punishment comes at the very end, in the form of a win or loss. Yet Samuel’s program was able to teach itself to play as well as most humans. It did not directly learn which move to make in each board position because that would have been too difficult. Rather, it learned how to evaluate each board position-how likely am I to win starting from this position?-and chose the move that led to the best position. Initially, the only positions it knew how to evaluate were the final ones: a win, a tie, or a loss. But once it knew that a certain position was a win, it also knew that positions from which it could move to it were good, and so on. Thomas J. Watson Sr., IBM’s president, predicted that when the program was demonstrated IBM stock would go up by fifteen points. It did. The lesson was not lost on IBM, which went on to build a chess champion and a Jeopardy! one.

The notion that not all states have rewards (positive or negative) but every state has a value is central to reinforcement learning. In board games, only final positions have a reward (1, 0, or ?1 for a win, tie, or loss, say). Other positions give no immediate reward, but they have value in that they can lead to rewards later. A chess position from which you can force checkmate in some number of moves is practically as good as a win and therefore has high value. We can propagate this kind of reasoning all the way to good and bad opening moves, even if at that distance the connection is far from obvious. In video games, the rewards are usually points, and the value of a state is the number of points you can accumulate starting from that state. In real life, a reward now is better than a reward later, so future rewards can be discounted by some rate of return, like investments. Of course, the rewards depend on what actions you choose, and the goal of reinforcement learning is to always choose the action that leads to the greatest rewards. Should you pick up the phone and ask your friend for a date? It could be the start of a beautiful relationship or just the route to a painful rejection. Even if your friend agrees to go on a date, that date may turn out well or not. Somehow, you have to abstract over all the infinite paths the future could take and make a decision now. Reinforcement learning does that by estimating the value of each state-the sum total of the rewards you can expect to get starting from that state-and choosing the actions that maximize it.

Suppose you’re moving along a tunnel, Indiana Jones-like, and you come to a fork. Your map says the left tunnel leads to a treasure and the right one to a snake pit. The value of where you’re standing-right before the fork-is the value of the treasure because you’ll choose to go left. If you always choose the best possible action, then the value of a state differs from the value of the succeeding state only by the immediate reward (if any) that you’ll get by performing that action. If we know each state’s immediate reward, we can use this observation to update the values of neighboring states, and so on, until all states have consistent values. The treasure’s value propagates backward along the tunnel until it reaches the fork and beyond. Once you know the value of each state, you also know which action to choose in each state (the one that maximizes the combination of immediate reward and value of the resulting state). This much was worked out in the 1950s by the control theorist Richard Bellman. But the real problem in reinforcement learning is when you don’t have a map of the territory. Then your only choice is to explore and discover what rewards are where. Sometimes you’ll discover a treasure, and other times you’ll fall into a snake pit. Every time you take an action, you note the immediate reward and the resulting state. That much could be done by supervised learning. But you also update the value of the state you just came from to bring it into line with the value you just observed, namely the reward you got plus the value of the new state you’re in. Of course, that value may not yet be the correct one, but if you wander around doing this for long enough, you’ll eventually settle on the right values for all the states and the corresponding actions. That’s reinforcement learning in a nutshell.

Notice how reinforcement learners face the same exploration-exploitation dilemma we met in Chapter 5: to maximize your rewards, you’ll naturally want to always pick the action leading to the highest-value state, but that prevents you from potentially discovering even higher rewards elsewhere. Reinforcement learners solve this by sometimes choosing the best action and sometimes a random one. (The brain even seems to have a “noise generator” for this purpose.) Early on, when there’s much to learn, it makes sense to explore a lot. Once you know the territory, it’s best to concentrate on exploiting it. That’s what humans do over their lifetimes: children explore, and adults exploit (except for scientists, who are eternal children). Children’s play is a lot more serious than it looks; if evolution made a creature that is helpless and a heavy burden on its parents for the first several years of its life, that extravagant cost must be for the sake of an even bigger benefit. In effect, reinforcement learning is a kind of speeded-up evolution-trying, discarding, and refining actions within a single lifetime instead of over generations-and by that standard it’s extremely efficient.

Research on reinforcement learning started in earnest in the early 1980s, with the work of Rich Sutton and Andy Barto at the University of Massachusetts. They felt that learning depends crucially on interacting with the environment, but supervised algorithms didn’t capture this, and they found inspiration instead in the psychology of animal learning. Sutton went on to become the leading proponent of reinforcement learning. Another key step happened in 1989, when Chris Watkins at Cambridge, initially motivated by his experimental observations of children’s learning, arrived at the modern formulation of reinforcement learning as optimal control in an unknown environment.

Reinforcement learners as we’ve seen them so far are not very realistic, however, because they don’t know what to do in a state unless they’ve been there before, and in the real world no two situations are ever exactly alike. We need to be able to generalize from previously visited states to new ones. Luckily, we already know how to do that: all we have to do is wrap reinforcement learning around one of the supervised learners we’ve met before, such as a multilayer perceptron. The neural network’s job is now to predict the value of a state, and the error signal for backpropagation is the difference between the predicted and observed values. There’s a problem, however. In supervised learning the target value for a state is always the same, but in reinforcement learning, it keeps changing as a consequence of updates to nearby states. As a result, reinforcement learning with generalization often fails to settle on a stable solution, unless the inner learner is something very simple, like a linear function. Nevertheless, reinforcement learning with neural networks has had some notable successes. An early one was a human-level backgammon player. More recently, a reinforcement learner from DeepMind, a London-based startup, beat an expert human player at Pong and other simple arcade games. It used a deep network to predict actions’ values from the console screen’s raw pixels. With its end-to-end vision, learning, and control, the system bore at least a passing resemblance to an artificial brain. This may help explain why Google paid half a billion dollars for DeepMind, a company with no products, no revenues, and few employees.

Gaming aside, researchers have used reinforcement learning to balance poles, control stick-figure gymnasts, park cars backward, fly helicopters upside down, manage automated telephone dialogues, assign channels in cell phone networks, dispatch elevators, schedule space-shuttle cargo loading, and much else. Reinforcement learning has also influenced psychology and neuroscience. The brain does it, using the neurotransmitter dopamine to propagate differences between expected and actual rewards. Reinforcement learning explains Pavlovian conditioning, but unlike behaviorism, it allows animals to have internal mental states. Foraging bees use it, as do mice finding cheese in mazes. Your daily life is a stream of little-noticed miracles made possible in part by reinforcement learning. You get up, get dressed, eat breakfast, and drive to work, all the while thinking about something else. Below the surface, reinforcement learning continually orchestrates and fine-tunes this prodigious symphony of motion. Snippets of reinforcement learning, also known as habits, make up most of what you do. You feel hungry, walk to the fridge, and grab a snack. As Charles Duhigg shows in The Power of Habit, understanding and controlling this cycle of cue, routine, and reward is key to success, not just for individuals but for businesses and even whole societies.

Of reinforcement learning’s founders, Rich Sutton is the most gung ho. For him, reinforcement learning is the Master Algorithm and solving it is tantamount to solving AI. Chris Watkins, on the other hand, is dissatisfied. He sees many things children can do that reinforcement learners can’t: solve problems, solve them better after a few attempts, make plans, acquire increasingly abstract knowledge. Luckily, we also have learning algorithms for these higher-level abilities, the most important of which is chunking.

Practice makes perfect

To learn is to get better with practice. You may barely remember it now, but learning to tie your shoelaces was really hard. At first you couldn’t do it at all, despite your five years of age. Then your laces probably came undone faster than you could tie them. But little by little you learned to tie them faster and better until it became completely automatic. The same happens with lots of other things, like crawling, walking, running, riding a bike, and driving a car; reading, writing, and arithmetic; playing an instrument and practicing a sport; cooking and using a computer. Ironically, you learn the most when it’s most painful: early on, when every step is difficult, you keep failing, and even when you succeed, the results are not very pretty. After you’ve mastered your golf swing or tennis serve, you can spend years perfecting it, but all those years make less difference than the first few weeks did. You get better with practice, but not at a constant rate: at first you improve quickly, then not so quickly, then very slowly. Whether it’s playing games or the guitar, the curve of performance improvement over time-how well you do something or how long it takes you to do it-has a very specific form:

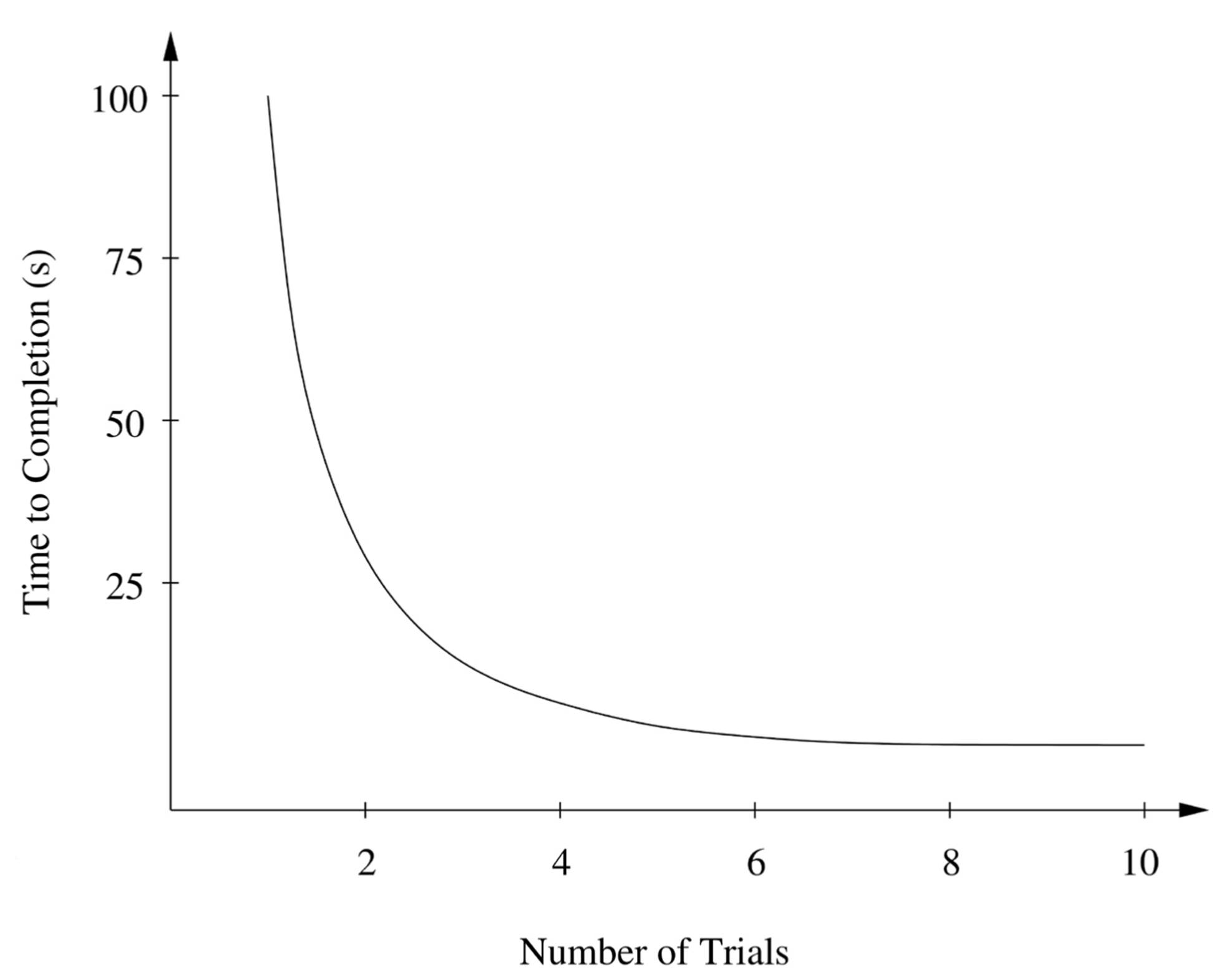
This type of curve is called a power law, because performance varies as time raised to some negative power. For example, in the figure above, time to completion is proportional to the number of trials raised to minus two (or equivalently, one over the number of trials squared). Pretty much every human skill follows a power law, with different powers for different skills. (In contrast, Windows never gets faster with practice-something for Microsoft to work on.)

In 1979, Allen Newell and Paul Rosenbloom started wondering what could be the reason for this so-called power law of practice. Newell was one of the founders of AI and a leading cognitive psychologist, and Rosenbloom was one of his graduate students at Carnegie Mellon University. At the time, none of the existing models of practice could explain the power law. Newell and Rosenbloom suspected it might have something to do with chunking, a concept from the psychology of perception and memory. We perceive and remember things in chunks, and we can only hold so many chunks in short-term memory at any given time (seven plus or minus two, according to the classic paper by George Miller). Crucially, grouping things into chunks allows us to process much more information than we otherwise could. That’s why telephone numbers have hyphens: 1-723-458-3897 is much easier to remember than 17234583897. Herbert Simon, Newell’s longtime collaborator and AI cofounder, had earlier found that the main difference between novice and expert chess players is that novices perceive chess positions one piece at a time while experts see larger patterns involving multiple pieces. Getting better at chess mainly involves acquiring more and larger such chunks. Newell and Rosenbloom hypothesized that a similar process is at work in all skill acquisition, not just chess.

In perception and memory, a chunk is just a symbol that stands for a pattern of other symbols, like AI stands for artificial intelligence. Newell and Rosenbloom adapted this notion to the theory of problem solving that Newell and Simon had developed earlier. Newell and Simon asked experimental subjects to solve problems-for example, derive one mathematical formula from another on the blackboard-while narrating aloud how they were going about it. They found that humans solve problems by decomposing them into subproblems, subsubproblems, and so on and systematically reducing the differences between the initial state (the first formula, say) and the goal state (the second formula). Doing so requires searching for a sequence of actions that will work, however, and that takes time. Newell and Rosenbloom’s hypothesis was that each time we solve a subproblem, we form a chunk that allows us to go directly from the state before we solve it to the state after. A chunk in this sense has two parts: the stimulus (a pattern you recognize in the external world or in your short-term memory) and the response (the sequence of actions you execute as a result). Once you’ve learned a chunk, you store it in long-term memory. Next time you have to solve the same subproblem, you can just apply the chunk, and save the time spent searching. This happens at all levels until you have a chunk for the whole problem and can solve it automatically. To tie your shoelaces, you tie the starting knot, make a loop with one end, wrap the other end around it, and pull it through the hole in the middle. Each of these is far from trivial for a five-year-old, but once you’ve acquired the corresponding chunks, you’re almost there.

Rosenbloom and Newell set their chunking program to work on a series of problems, measured the time it took in each trial, and lo and behold, out popped a series of power law curves. But that was only the beginning. Next they incorporated chunking into Soar, a general theory of cognition that Newell had been working on with John Laird, another one of his students. Instead of working only within a predefined hierarchy of goals, the Soar program could define and solve a new subproblem every time it hit a snag. Once it formed a new chunk, Soar generalized it to apply to similar problems, in a manner similar to inverse deduction. Chunking in Soar turned out to be a good model of lots of learning phenomena besides the power law of practice. It could even be applied to learning new knowledge by chunking data and analogies. This led Newell, Rosenbloom, and Laird to hypothesize that chunking is the only mechanism needed for learning-in other words, the Master Algorithm.

Being classic AI types, Newell, Simon, and their students and followers were strong believers in the primacy of problem solving. If the problem solver is powerful, the learner can piggyback on it and be simple. Indeed, learning is just another kind of problem solving. Newell and company made a concerted effort to reduce all learning to chunking and all cognition to Soar, but in the end they failed. One problem was that, as the problem solver learned more chunks, and more complicated ones, the cost of trying them often became so high that the program got slower instead of faster. Somehow humans avoid this, but so far researchers in this area have not figured out how. On top of that, trying to reduce reinforcement learning, supervised learning, and everything else to chunking ultimately created more problems than it solved. Eventually, the Soar researchers conceded defeat and incorporated those other types of learning into Soar as separate mechanisms. Nevertheless, chunking remains a preeminent example of a learning algorithm inspired by psychology, and the true Master Algorithm, whatever it turns out to be, must surely share its ability to improve with practice.

Chunking and reinforcement learning are not as widely used in business as supervised learning, clustering, or dimensionality reduction, but a simpler type of learning by interacting with the environment is: learning the effects of your actions (and acting accordingly). If the background color of your e-commerce site’s home page is currently blue and you’re wondering whether making it red would increase sales, try it out on a hundred thousand randomly chosen customers and compare the results with those of the regular site. This technique, called A/B testing, was at first used mainly in drug trials but has since spread to many fields where data can be gathered on demand, from marketing to foreign aid. It can also be generalized to try many combinations of changes at once, without losing track of which changes lead to which gains (or losses). Companies like Amazon and Google swear by it; you’ve probably participated in thousands of A/B tests without realizing it. A/B testing gives the lie to the oft-heard criticism that big data is only good for finding correlations, not causation. Philosophical fine points aside, learning causality is learning the effects of your actions, and anyone with a stream of data they can affect can do it-from a one-year-old splashing around in the bathtub to a president campaigning for reelection.

Learning to relate

If we endow Robby the robot with all the learning abilities we’ve seen so far in this book, he’ll be pretty smart but still a bit autistic. He’ll see the world as a bunch of separate objects, which he can identify, manipulate, and even make predictions about, but he won’t understand that the world is a web of interconnections. Robby the doctor would be very good at diagnosing someone with the flu based on his symptoms but unable to suspect that the patient has swine flu because he has been in contact with someone infected with it. Before Google, search engines decided whether a web page was relevant to your query by looking at its content-what else? Brin and Page’s insight was that the strongest sign a page is relevant is that relevant pages link to it. Similarly, if you want to predict whether a teenager is at risk of starting to smoke, by far the best thing you can do is check whether her close friends smoke. An enzyme’s shape is as inseparable from the shapes of the molecules it brings together as a lock is from its key. Predator and prey have deeply entwined properties, each evolved to defeat the other’s properties. In all of these cases, the best way to understand an entity-whether it’s a person, an animal, a web page, or a molecule-is to understand how it relates to other entities. This requires a new kind of learning that doesn’t treat the data as a random sample of unrelated objects but as a glimpse into a complex network. Nodes in the network interact; what you do to one affects the others and comes back to affect you. Relational learners, as they’re called, may not quite have social intelligence, but they’re the next best thing. In traditional statistical learning, every man is an island, entire of itself. In relational learning, every man is a piece of the continent, a part of the main. Humans are relational learners, wired to connect, and if we want Robby to grow into a perceptive, socially adept robot, we need to wire him to connect, too.

The first difficulty we face is that, when the data is all one big network, we no longer seem to have many examples to learn from, just one-and that’s not enough. Na?ve Bayes learns that a fever is a symptom of the flu by counting the number of fever-stricken flu patients. If it could only see one patient, it would either conclude that flu always causes fever or that it never does, both of which are wrong. We would like to learn that the flu is contagious by looking at the pattern of infections in a social network-a clump of infected people here, a clump of uninfected ones there-but we only have one pattern to look at, even if it’s in a network of seven billion people, so it’s not clear how to generalize. The key is to notice that, embedded in that big network, we have many examples of pairs of people. If acquaintances are more likely to both have the flu than pairs of people who have never met, then being acquainted with a flu patient makes you more likely to be one as well. Unfortunately, however, we can’t just count how many pairs of acquaintances in the data both have the flu and turn those counts into probabilities. This is because a person has many acquaintances, and all the pairwise probabilities don’t add up to a coherent model that lets us, for example, compute how likely someone is to have the flu given which of their acquaintances do. We didn’t have this problem when the examples were all separate, and we wouldn’t have it in, say, a society of childless couples, each living on their own desert island. But that’s not the real world, and there wouldn’t be any epidemics in it, anyway.

The solution is to have a set of features and learn their weights, as in Markov networks. For every person X, we can have the feature X has the flu; for every pair of acquaintances X and Y, the feature X and Y both have the flu; and so on. As in Markov networks, the maximum-likelihood weights are the ones that make each feature occur with the frequency observed in the data. The weight of X has the flu will be high if a lot of people have the flu. The weight of X and Y both have the flu will be high if, when person X has the flu, the odds that acquaintance Y also has the flu are higher than for a randomly chosen member of the network. If 40 percent of people have the flu and so do 16 percent of all acquaintance pairs, then the weight of X and Y both have the flu will be zero, because we don’t need that feature to correctly reproduce the data’s statistics (0.4 ? 0.4 = 0.16). But if the feature has a positive weight, flu is more likely to occur in clumps than to just infect people at random, and you’re more likely to have the flu if your acquaintances do.

Notice that the network has a separate feature for each pair of people: Alice and Bob both have the flu, Alice and Chris both have the flu, and so on. But we can’t learn a separate weight for each pair, because we only have one data point per pair (whether it’s infected or not), and we wouldn’t be able to generalize to members of the network we haven’t diagnosed yet (do Yvette and Zach both have the flu?). What we can do instead is learn a single weight for all features of the same form, based on all the instances of it that we’ve seen. In effect, X and Y have the flu is a template for features that can be instantiated with each pair of acquaintances (Alice and Bob, Alice and Chris, etc.). The weights for all the instances of a template are “tied together,” in the sense that they all have the same value, and that’s how we can generalize despite having only one example (the whole network). In nonrelational learning, the parameters of a model are tied in only one way: across all the independent examples (e.g., all the patients we’ve diagnosed). In relational learning, every feature template we create ties the parameters of all its instances.

We’re not limited to pairwise or individual features. Facebook wants to predict who your friends are so it can recommend them to you. It can use the rule Friends of friends are likely to be friends for that, but each instance of it involves three people: if Alice and Bob are friends, and Bob and Chris are also friends, then Alice and Chris are potential friends. H. L. Mencken’s quip that a man is wealthy if he makes more than his wife’s sister’s husband involves four people. Each of these rules can be turned into a feature template in a relational model, and a weight for it can be learned based on how often the feature occurs in the data. As in Markov networks, the features themselves can also be learned from the data.

Relational learners can generalize from one network to another (e.g., learn a model of how flu spreads in Atlanta and apply it in Boston). They can also learn on more than one network (e.g., Atlanta and Boston, assuming, unrealistically, that no one in Atlanta is ever in contact with anyone in Boston). But unlike “regular” learning, where all examples must have exactly the same number of attributes, in relational learning networks can vary in size; a larger network will just have more instances of the same templates than a smaller one. Of course, the generalization from a smaller network to a larger one may or may not be accurate, but the point is that nothing prevents it; and large networks often do behave locally like small ones.

The neatest trick a relational learner can do is to turn a sporadic teacher into an assiduous one. For an ordinary classifier, examples without classes are useless. If I’m given a patient’s symptoms, but not the diagnosis, that doesn’t help me learn to diagnose. But if I know that some of the patient’s friends have the flu, that’s indirect evidence that he may have the flu as well. Diagnosing a few people in a network and then propagating those diagnoses to their friends, and their friends’ friends, is the next best thing to diagnosing everyone. The inferred diagnoses may be noisy, but the overall statistics of how symptoms correlate with the flu will probably be a lot more accurate and complete than if I had only a handful of isolated diagnoses to draw on. Children are very good at making the most of the sporadic supervision they get (provided they don’t choose to ignore it). Relational learners share some of that ability.

All this power comes at a cost, however. In an ordinary classifier, such as a decision tree or a perceptron, inferring an entity’s class from its attributes is a matter of a few lookups and a bit of arithmetic. In a network, each node’s class depends indirectly on all the others’, and we can’t infer it in isolation. We can resort to the same kinds of inference techniques we used for Bayesian networks, like loopy belief propagation or MCMC, but the scale is different. A typical Bayesian network has perhaps thousands of variables, but a typical social network has millions of nodes or more. Luckily, because the model of the network consists of many repetitions of the same features with the same weights, we can often condense the network into “supernodes,” each consisting of many nodes that we know will have the same probabilities, and solve a much smaller problem with the same result.

Relational learning has a long history, going back to at least the seventies and symbolist techniques like inverse deduction. But it acquired a new impetus with the advent of the Internet. Suddenly networks were everywhere, and modeling them was urgent. One phenomenon I found particularly intriguing was word of mouth. How does information propagate in a social network? Can we measure each member’s influence and target just enough of the most influential members to set off a wave of word of mouth? With my student Matt Richardson, I designed an algorithm that did just that. We applied it to Epinions, a product review site that allowed members to say whose reviews they trusted. We found, among other things, that marketing a product to the single most influential member-trusted by many followers who were in turn trusted by many others, and so on-was as good as marketing to a third of all the members in isolation. An avalanche of other research on this problem followed. Since then, I’ve applied relational learning to many others, including predicting who will form links in a social network, integrating databases, and enabling robots to build maps of their surroundings.

If you want to understand how the world works, relational learning is a good tool to have. In Isaac Asimov’s Foundation, the scientist Hari Seldon manages to mathematically predict the future of humanity and thereby save it from decadence. Paul Krugman, among others, has confessed that this seductive dream was what made him become an economist. According to Seldon, people are like molecules in a gas, and the law of large numbers ensures that even if individuals are unpredictable, whole societies aren’t. Relational learning reveals why this is not the case. If people were independent, each making decisions in isolation, societies would indeed be predictable, because all those random decisions would add up to a fairly constant average. But when people interact, larger assemblies can be less predictable than smaller ones, not more. If confidence and fear are contagious, each will dominate for a while, but every now and then an entire society will swing from one to the other. It’s not all bad news, though. If we can measure how strongly people influence each other, we can estimate how long it will be before a swing occurs, even if it’s the first one-another way in which black swans are not necessarily unpredictable.

A common complaint about big data is that the more data you have, the easier it is to find spurious patterns in it. This may be true if the data is just a huge set of disconnected entities, but if they’re interrelated, the picture changes. For example, critics of using data mining to catch terrorists argue that, ethical issues aside, it will never work because there are too many innocents and too few terrorists and so mining for suspicious patterns will either cause too many false alarms or never catch anyone. Is someone videotaping the New York City Hall a tourist or a terrorist scoping out a bombing site? And is someone buying large quantities of ammonium nitrate a farmer or a bomb maker? Each of these looks innocent enough in isolation, but if the “tourist” and the “farmer” have been in close phone contact, and the latter just drove his heavily laden pickup into Manhattan, maybe it’s time for someone to take a closer look. The NSA likes to mine records of who called whom not just because it’s arguably legal, but because they’re often more informative to the prediction algorithms than the content of the calls, which it would take a human to understand.

Social networks aside, the killer app of relational learning is understanding how living cells work. A cell is a complex metabolic network with genes coding for proteins that regulate other genes, long interlocking chains of chemical reactions, and products migrating from one organelle to another. Independent entities, doing their work in isolation, are nowhere to be seen. A cancer drug must disrupt cancer cells’ workings without interfering with normal ones’. If we have an accurate relational model of both, we can try many different drugs in silico, letting the model infer their good and bad effects and keeping only the best ones to try in vitro and finally in vivo.

Like human memory, relational learning weaves a rich web of associations. It connects percepts, which a robot like Robby can acquire by clustering and dimensionality reduction, with skills, which he can learn by reinforcement and chunking, and with the higher-level knowledge that comes from reading, going to school, and interacting with humans. Relational learning is the last piece of the puzzle, the final ingredient we need for our alchemy. And now it’s time to repair to the lab and transmute all these elements into the Master Algorithm.

Оглавление книги