Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER THREE: Hume’s Problem of Induction

CHAPTER THREE: Hume’s Problem of Induction

Are you a rationalist or an empiricist?

Rationalists believe that the senses deceive and that logical reasoning is the only sure path to knowledge. Empiricists believe that all reasoning is fallible and that knowledge must come from observation and experimentation. The French are rationalists; the Anglo-Saxons (as the French call them) are empiricists. Pundits, lawyers, and mathematicians are rationalists; journalists, doctors, and scientists are empiricists. Murder, She Wrote is a rationalist TV crime show; CSI: Crime Scene Investigation is an empiricist one. In computer science, theorists and knowledge engineers are rationalists; hackers and machine learners are empiricists.

The rationalist likes to plan everything in advance before making the first move. The empiricist prefers to try things and see how they turn out. I don’t know if there’s a gene for rationalism or one for empiricism, but looking at my computer scientist colleagues, I’ve observed time and again that they are almost like personality traits: some people are rationalistic to the core and could never have been otherwise; and others are empiricist through and through, and that’s what they’ll always be. The two sides can converse with each other and sometimes draw on each other’s results, but they can understand each other only so much. Deep down each believes that what the other does is secondary, and not very interesting.

Rationalists and empiricists have probably been around since the dawn of Homo sapiens. Before setting out on a hunt, Caveman Bob spent a long time sitting in his cave figuring out where the game would be. In the meantime, Cavewoman Alice was out systematically surveying the territory. Since both kinds are still with us, it’s probably safe to say that neither approach was better. You might think that machine learning is the final triumph of the empiricists, but the truth is more subtle, as we’ll soon see.

Rationalism versus empiricism is a favorite question of philosophers. Plato was an early rationalist, and Aristotle an early empiricist. But the debate really took off during the Enlightenment, with a trio of great thinkers on each side: Descartes, Spinoza, and Leibniz were the leading rationalists; Locke, Berkeley, and Hume were their empiricist counterparts. Trusting in their powers of reasoning, the rationalists concocted theories of the universe that-to put it gently-did not stand the test of time, but they also invented fundamental mathematical techniques like calculus and analytical geometry. The empiricists were altogether more practical, and their influence is everywhere from the scientific method to the Constitution of the United States.

David Hume was the greatest of the empiricists and the greatest English-speaking philosopher of all time. Thinkers like Adam Smith and Charles Darwin count him among their key influences. You could also say he’s the patron saint of the symbolists. He was born in Scotland in 1711 and spent most of his life in eighteenth-century Edinburgh, a prosperous city full of intellectual ferment. A man of genial disposition, he was nevertheless an exacting skeptic who spent much of his time debunking the myths of his age. He also took the empiricist train of thought that Locke had started to its logical conclusion and asked a question that has since hung like a sword of Damocles over all knowledge, from the most trivial to the most advanced: How can we ever be justified in generalizing from what we’ve seen to what we haven’t? Every learning algorithm is, in a sense, an attempt to answer this question.

Hume’s question is also the departure point for our journey. We’ll start by illustrating it with an example from daily life and meeting its modern embodiment in the famous “no free lunch” theorem. Then we’ll see the symbolists’ answer to Hume. This leads us to the most important problem in machine learning: overfitting, or hallucinating patterns that aren’t really there. We’ll see how the symbolists solve it, and how machine learning is at heart a kind of alchemy, transmuting data into knowledge with the aid of a philosopher’s stone. For the symbolists, the philosopher’s stone is knowledge itself. In the next four chapters we’ll study the solutions of the other tribes’ alchemists.

To date or not to date?

You have a friend you really like, and you want to ask her out on a date. You have a hard time dealing with rejection, though, and you’re only going to ask her if you’re pretty sure she’ll say yes. It’s Friday evening, and there you sit with cell phone in hand, trying to decide whether or not to call her. You remember that the previous time you asked her, she said no. But why? Two times before that she said yes, and the one before those she said no. Maybe there are days she doesn’t like to go out? Or maybe she likes clubbing but not dinner dates? Being of an unusually systematic nature, you put down the phone and jot down what you can remember about those previous occasions:

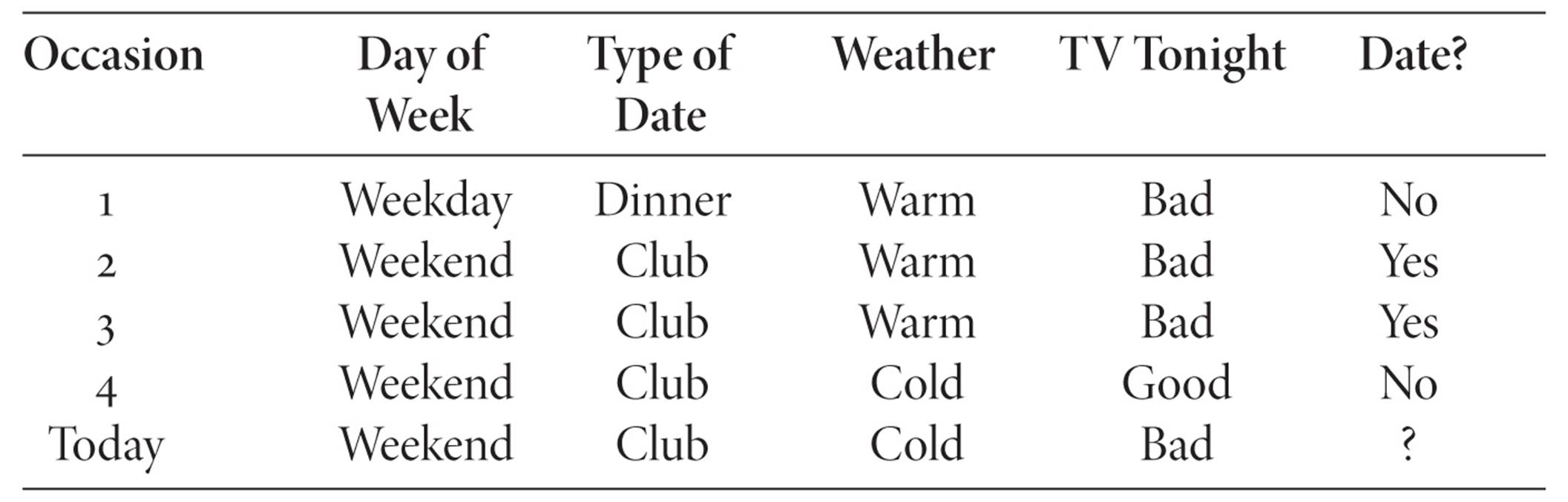
So… what shall it be? Date or no date? Is there a pattern that distinguishes the yeses from the nos? And, most important, what does that pattern say about today?

Clearly, there’s no single factor that correctly predicts the answer: on some weekends she likes to go out, and on some she doesn’t; sometimes she likes to go clubbing, and sometimes she doesn’t, and so on. What about a combination of factors? Maybe she likes to go clubbing on weekends? No, occasion number 4 crosses that one out. Or maybe she only likes to go out on warm weekend nights? Bingo! That works! In which case, looking at the frosty weather outside, tonight doesn’t look promising. But wait! What if she likes to go clubbing when there’s nothing good on TV? That also works, and that means today is a yes! Quick, call her before it gets too late. But wait a second. How do you know this is the right pattern? You’ve found two that agree with your previous experience, but they make opposite predictions. Come to think of it, what if she only goes clubbing when the weather is nice? Or she goes out on weekends when there’s nothing to watch on TV? Or-

At this point you crumple your notes in frustration and fling them into the wastebasket. There’s no way to know! What can you do? The ghost of Hume nods sadly over your shoulder. You have no basis to pick one generalization over another. Yes and no are equally legitimate answers to the question “What will she say?” And the clock is ticking. Bitterly, you fish out a quarter from your pocket and prepare to flip it.

You’re not the only one in dire straits-so are we. We’ve only just set out on our road to the Master Algorithm and already we seem to have run into an insurmountable obstacle. Is there any way to learn something from the past that we can be confident will apply in the future? And if there isn’t, isn’t machine learning a hopeless enterprise? For that matter, isn’t all of science, even all of human knowledge, on rather shaky ground?

It’s not like big data would solve the problem. You could be super-Casanova and have dated millions of women thousands of times each, but your master database still wouldn’t answer the question of what this woman is going to say this time. Even if today is exactly like some previous occasion when she said yes-same day of week, same type of date, same weather, and same shows on TV-that still doesn’t mean that this time she will say yes. For all you know, her answer is determined by some factor that you didn’t think of or don’t have access to. Or maybe there’s no rhyme or reason to her answers: they’re random, and you’re just spinning your wheels trying to find a pattern in them.

Philosophers have debated Hume’s problem of induction ever since he posed it, but no one has come up with a satisfactory answer. Bertrand Russell liked to illustrate the problem with the story of the inductivist turkey. On his first morning at the farm, the turkey was fed at 9:00 a.m., but being a good inductivist, he didn’t jump to conclusions. He first collected many observations on many different days under many different circumstances. Having been fed consistently at 9:00 a.m. for many consecutive days, he finally concluded that yes, he would always be fed at 9:00 a.m. Then came the morning of Christmas eve, and his throat was cut.

It would be nice if Hume’s problem was just a cute philosophical conundrum we could ignore, but we can’t. For example, Google’s business is based on guessing which web pages you’re looking for when you type some keywords into the search box. Their key asset is massive logs of search queries people have entered in the past and the links they clicked on in the corresponding results pages. But what do you do if someone types in a combination of keywords that’s not in the log? And even if it is, how can you be confident that the current user wants the same pages as the previous ones?

How about we just assume that the future will be like the past? This is certainly a risky assumption. (It didn’t work for the inductivist turkey.) On the other hand, without it all knowledge is impossible, and so is life. We’d rather stay alive, even if precariously. Unfortunately, even with that assumption we’re not out of the woods. It takes care of the “trivial” cases: If I’m a doctor and patient B has exactly the same symptoms as patient A, I assume that the diagnosis is the same. But if patient B’s symptoms don’t exactly match anyone else’s, I’m still in the dark. This is the machine-learning problem: generalizing to cases that we haven’t seen before.

But perhaps that’s not such a big deal? With enough data, won’t most cases be in the “trivial” category? No. We saw in the previous chapter why memorization won’t work as a universal learner, but now we can make it more quantitative. Suppose you have a database with a trillion records, each with a thousand Boolean fields (i.e., each field is the answer to a yes/no question). That’s pretty big. What fraction of the possible cases have you seen? (Take a guess before you read on.) Well, the number of possible answers is two for each question, so for two questions it’s two times two (yes-yes, yes-no, no-yes, and no-no), for three questions it’s two cubed (2 ? 2 ? 2 = 2³), and for a thousand questions it’s two raised to the power of a thousand (2¹⁰⁰⁰). The trillion records in your database are one-gazillionth of 1 percent of 2¹⁰⁰⁰, where “gazillionth” means “zero point 286 zeros followed by 1.” Bottom line: no matter how much data you have-tera- or peta- or exa- or zetta- or yottabytes-you’ve basically seen nothing. The chances that the new case you need to make a decision on is already in the database are so vanishingly small that, without generalization, you won’t even get off the ground.

If this all sounds a bit abstract, suppose you’re a major e-mail provider, and you need to label each incoming e-mail as spam or not spam. You may have a database of a trillion past e-mails, each already labeled as spam or not, but that won’t save you, since the chances that every new e-mail will be an exact copy of a previous one are just about zero. You have no choice but to try to figure out at a more general level what distinguishes spam from nonspam. And, according to Hume, there’s no way to do that.

The “no free lunch” theorem

Two hundred and fifty years after Hume set off his bombshell, it was given elegant mathematical form by David Wolpert, a physicist turned machine learner. His result, known as the “no free lunch” theorem, sets a limit on how good a learner can be. The limit is pretty low: no learner can be better than random guessing! OK, we can go home: the Master Algorithm is just flipping coins. Seriously, though, how is it that no learner can beat coin flipping? And if that’s so, how come the world is full of highly successful learners, from spam filters to (any day now) self-driving cars?

The “no free lunch” theorem is a lot like the reason Pascal’s wager fails. In his Pens?es, published in 1669, Pascal said we should believe in the Christian God because if he exists that gains us eternal life, and if he doesn’t we lose very little. This was a remarkably sophisticated argument for the time, but as Diderot pointed out, an imam could make the same argument for believing in Allah. And if you pick the wrong god, the price you pay is eternal hell. On balance, considering the wide variety of possible gods, you’re no better off picking a particular one to believe in than you are picking any other. For every god that says “do this,” there’s another that says “no, do that.” You may as well just forget about god and enjoy life without religious constraints.

Replace “god” with “learning algorithm” and “eternal life” with “accurate prediction,” and you have the “no free lunch” theorem. Pick your favorite learner. (We’ll see many in this book.) For every world where it does better than random guessing, I, the devil’s advocate, will deviously construct one where it does worse by the same amount. All I have to do is flip the labels of all unseen instances. Since the labels of the observed ones agree, there’s no way your learner can distinguish between the world and the antiworld. On average over the two, it’s as good as random guessing. And therefore, on average over all possible worlds, pairing each world with its antiworld, your learner is equivalent to flipping coins.

Don’t give up on machine learning or the Master Algorithm just yet, though. We don’t care about all possible worlds, only the one we live in. If we know something about the world and incorporate it into our learner, it now has an advantage over random guessing. To this Hume would reply that that knowledge must itself have come from induction and is therefore fallible. That’s true, even if the knowledge was encoded into our brains by evolution, but it’s a risk we’ll have to take. We can also ask whether there’s a nugget of knowledge so incontestable, so fundamental, that we can build all induction on top of it. (Something like Descartes’ “I think, therefore I am,” although it’s hard to see how to turn that one into a learning algorithm.) I think the answer is yes, and we’ll see what that nugget is in Chapter 9.

In the meantime, the practical consequence of the “no free lunch” theorem is that there’s no such thing as learning without knowledge. Data alone is not enough. Starting from scratch will only get you to scratch. Machine learning is a kind of knowledge pump: we can use it to extract a lot of knowledge from data, but first we have to prime the pump.

Machine learning is what mathematicians call an ill-posed problem: it doesn’t have a unique solution. Here’s a simple ill-posed problem: Which two numbers add up to 1,000? Assuming the numbers are positive, there are five hundred possible answers: 1 and 999, 2 and 998, and so on. The only way to solve an ill-posed problem is to introduce additional assumptions. If I tell you the second number is triple the first, bingo: the answer is 250 and 750.

Tom Mitchell, a leading symbolist, calls it “the futility of bias-free learning.” In ordinary life, bias is a pejorative word: preconceived notions are bad. But in machine learning, preconceived notions are indispensable; you can’t learn without them. In fact, preconceived notions are also indispensable to human cognition, but they’re hardwired into the brain, and we take them for granted. It’s biases over and beyond those that are questionable.

Aristotle said that there is nothing in the intellect that was not first in the senses. Leibniz added, “Except the intellect itself.” The human brain is not a blank slate because it’s not a slate. A slate is passive, something you write on, but the brain actively processes the information it receives. Memory is the slate it writes on, and it does start out blank. On the other hand, a computer is a blank slate until you program it; the active process itself has to be written into memory before anything can happen. Our goal is to figure out the simplest program we can write such that it will continue to write itself by reading data, without limit, until it knows everything there is to know.

Machine learning has an unavoidable element of gambling. In the first Dirty Harry movie, Clint Eastwood chases a bank robber, repeatedly firing at him. Finally, the robber is lying next to a loaded gun, unsure whether to spring for it. Did Harry fire six shots or only five? Harry sympathizes (so to speak): “You’ve got to ask yourself one question: ‘Do I feel lucky?’ Well, do you, punk?” That’s the question machine learners have to ask themselves every day when they go to work: Do I feel lucky today? Just like evolution, machine learning doesn’t get it right every time; in fact, errors are the rule, not the exception. But it’s OK, because we discard the misses and build on the hits, and the cumulative result is what matters. Once we acquire a new piece of knowledge, it becomes a basis for inducing yet more knowledge. The only question is where to begin.

Priming the knowledge pump

In the Principia, along with his three laws of motion, Newton enunciates four rules of induction. Although these are much less well known than the physical laws, they are arguably as important. The key rule is the third one, which we can paraphrase thus:

Newton’s Principle: Whatever is true of everything we’ve seen is true of everything in the universe.

It’s not an exaggeration to say that this innocuous-sounding statement is at the heart of the Newtonian revolution and of modern science. Kepler’s laws applied to exactly six entities: the planets of the solar system known in his time. Newton’s laws apply to every last speck of matter in the universe. The leap in generality between the two is staggering, and it’s a direct consequence of Newton’s principle. This one principle is all by itself a knowledge pump of phenomenal power. Without it there would be no laws of nature, only a forever incomplete patchwork of small regularities.

Newton’s principle is the first unwritten rule of machine learning. We induce the most widely applicable rules we can and reduce their scope only when the data forces us to. At first sight this may seem ridiculously overconfident, but it’s been working for science for over three hundred years. It’s certainly possible to imagine a universe so varied and capricious that Newton’s principle would systematically fail, but that’s not our universe.

Newton’s principle is only the first step, however. We still need to figure out what is true of everything we’ve seen-how to extract the regularities from the raw data. The standard solution is to assume we know the form of the truth, and the learner’s job is to flesh it out. For example, in the dating problem you could assume that your friend’s answer is determined by a single factor, in which case learning just consists of checking each known factor (day of week, type of date, weather, and TV programming) to see if it correctly predicts her answer every time. The problem, of course, is that none of them do! You gambled and failed. So you relax your assumptions a bit. What if your friend’s answer is determined by a conjunction of two factors? With four factors, each with two possible values, there are twenty-four possibilities to check (six pairs of factors to pick from times two choices for each factor’s value). Now we have an embarrassment of riches: four conjunctions of two factors correctly predict the outcome! What to do? If you’re feeling lucky, you can just pick one of them and hope for the best. A more sensible option, though, is democracy: let them vote, and pick the winning prediction.

If all conjunctions of two factors fail, you can try all conjunctions of any number of factors. Machine learners and psychologists call these “conjunctive concepts.” Dictionary definitions are conjunctive concepts: a chair has a seat and a back and some number of legs. Remove any of these and it’s no longer a chair. A conjunctive concept is what Tolstoy had in mind when he wrote the opening sentence of Anna Karenina: “All happy families are alike; each unhappy family is unhappy in its own way.” The same is true of individuals. To be happy, you need health, love, friends, money, a job you like, and so on. Take any of these away, and misery ensues.

In machine learning, examples of a concept are called positive examples, and counterexamples are called negative examples. If you’re trying to learn to recognize cats in images, images of cats are positive examples and images of dogs are negative ones. If you compiled a database of families from the world’s literature, the Karenins would be a negative example of a happy family, and there would be precious few positive examples.

Starting with restrictive assumptions and gradually relaxing them if they fail to explain the data is typical of machine learning, and the process is usually carried out automatically by the learner, without any help from you. First, it tries all single factors, then all conjunctions of two factors, then all conjunctions of three, and so on. But now we run into a problem: there are a lot of conjunctive concepts and not enough time to try them all out.

The dating example is a little deceptive because it’s very small (four variables and four examples). But suppose now that you run an online dating service and you need to figure out which couples to match. If each user of your system has filled out a questionnaire with answers to fifty yes/no questions, each potential match is characterized by one hundred attributes, fifty from each member of the prospective couple. Based on the couples that have gone on a date and reported the outcome, can you find a conjunctive definition for the concept of a “good match”? There are 3¹⁰⁰ possible definitions to try. (The three options for each attribute are yes, no, and not part of the concept.) Even with the fastest computer in the world, the couples will all be long gone-and your company bankrupt-by the time you’re done, unless you’re lucky and a very short definition hits the jackpot. So many rules, so little time. We need to do something smarter.

Here’s one way. Suspend your disbelief and start by assuming that all matches are good. Then try excluding all matches that don’t have some attribute. Repeat this for each attribute, and choose the one that excludes the most bad matches and the fewest good ones. Your definition now looks something like, say, “It’s a good match only if he’s outgoing.” Now try adding every other attribute to that in turn, and choose the one that excludes the most remaining bad matches and fewest remaining good ones. Perhaps the definition is now “It’s a good match only if he’s outgoing and so is she.” Try adding a third attribute to those two, and so on. Once you’ve excluded all the bad matches, you’re done: you have a definition of the concept that includes all the positive examples and excludes all the negative ones. For example: “A couple is a good match only if they’re both outgoing, he’s a dog person, and she’s not a cat person.” You can now throw away the data and keep only this definition, since it encapsulates all that’s relevant for your purposes. This algorithm is guaranteed to finish in a reasonable amount of time, and it’s also the first actual learner we meet in this book!

How to rule the world

Conjunctive concepts don’t get you very far, though. The problem is that, as Rudyard Kipling said, “There are nine and sixty ways of constructing tribal lays, and every one of them is right.” Real concepts are disjunctive. Chairs can have four legs or one, and sometimes none. You can win at chess in countless different ways. E-mails containing the word Viagra are probably spam, but so are e-mails containing “FREE!!!” Besides, all rules have exceptions. Some families manage to be dysfunctional yet happy. Birds fly, unless they’re penguins, ostriches, cassowaries, or kiwis (or they’ve broken a wing, or are locked in a cage, or…).

What we need is to learn concepts that are defined by a set of rules, not just a single rule, such as:

If you liked Star Wars, episodes IV-VI, you’ll like Avatar.

If you liked Star Trek: The Next Generation and Titanic, you’ll like Avatar.

If you’re a member of the Sierra Club and read science-fiction books, you’ll like Avatar.

Or:

If your credit card was used in China, Canada, and Nigeria yesterday, it was stolen.

If your credit card was used twice after 11:00 p.m. on a weekday, it was stolen.

If your credit card was used to purchase one dollar of gas, it was stolen.

(If you’re wondering about the last rule, credit-card thieves used to routinely buy one dollar of gas to check that a stolen credit card was good before data miners caught on to the tactic.)

We can learn sets of rules like this one rule at a time, using the algorithm we saw before for learning conjunctive concepts. After we learn each rule, we discard the positive examples that it accounts for, so the next rule tries to account for as many of the remaining positive examples as possible, and so on until all are accounted for. It’s an example of “divide and conquer,” the oldest strategy in the scientist’s playbook. We can also improve the algorithm for finding a single rule by keeping some number n of hypotheses around, not just one, and at each step extending all of them in all possible ways and keeping the n best results.

Discovering rules in this way was the brainchild of Ryszard Michalski, a Polish computer scientist. Michalski’s hometown of Kalusz was successively part of Poland, Russia, Germany, and Ukraine, which may have left him more attuned than most to disjunctive concepts. After immigrating to the United States in 1970, he went on to found the symbolist school of machine learning, along with Tom Mitchell and Jaime Carbonell. He had an imperious personality. If you gave a talk at a machine-learning conference, the odds were good that at the end he’d raise his hand to point out that you had just rediscovered one of his old ideas.

Sets of rules are popular with retailers who are deciding which goods to stock. Typically, they use a more exhaustive approach than “divide and conquer,” looking for all rules that strongly predict the purchase of each item. Walmart was a pioneer in this area. One of their early findings was that if you buy diapers you are also likely to buy beer. Huh? One interpretation of this is that Mom sends Dad to the supermarket to buy diapers, and as emotional compensation, Dad buys a case of beer to go with them. Knowing this, the supermarket can now sell more beer by putting it next to the diapers, which would never have occurred to it without rule mining. The “beer and diapers” rule has acquired legendary status among data miners (although some claim the legend is of the urban variety). Either way, it’s a long way from the digital circuit design problems Michalski had in mind when he first started thinking about rule induction in the 1960s. When you invent a new learning algorithm, you can’t even begin to imagine all the things it will be used for.

My first direct experience of rule learning in action was when, having just moved to the United States to start graduate school, I applied for a credit card. The bank sent me a letter saying “We regret that your application has been rejected due to INSUFFICIENT-TIME-AT-CURRENT-ADDRESS and NO-PREVIOUS-CREDIT-HISTORY” (or some other all-cap words to that effect). I knew right then that there was much research left to do in machine learning.

Between blindness and hallucination

Sets of rules are vastly more powerful than conjunctive concepts. They’re so powerful, in fact, that you can represent any concept using them. It’s not hard to see why. If you give me a complete list of all the instances of a concept, I can just turn each instance into a rule that specifies all attributes of that instance, and the set of all those rules is the definition of the concept. Going back to the dating example, one rule would be: If it’s a warm weekend night, there’s nothing good on TV, and you propose going to a club, she’ll say yes. The table only contains a few examples, but if it contained all 2 ? 2 ? 2 ? 2 = 16 possible ones, with each labeled “Date” or “No date,” turning each positive example into a rule in this way would do the trick.

The power of rule sets is a double-edged sword. On the upside, you know you can always find a rule set that perfectly matches the data. But before you start feeling lucky, realize that you’re at severe risk of finding a completely meaningless one. Remember the “no free lunch” theorem: you can’t learn without knowledge. And assuming that the concept can be defined by a set of rules is tantamount to assuming nothing.

An example of a useless rule set is one that just covers the exact positive examples you’ve seen and nothing else. This rule set looks like it’s 100 percent accurate, but that’s an illusion: it will predict that every new example is negative, and therefore get every positive one wrong. If there are more positive than negative examples overall, this will be even worse than flipping coins. Imagine a spam filter that decides an e-mail is spam only if it’s an exact copy of a previously labeled spam message. It’s easy to learn and looks great on the labeled data, but you might as well have no spam filter at all. Unfortunately, our “divide and conquer” algorithm could easily learn a rule set like that.

In his story “Funes the Memorious,” Jorge Luis Borges tells of meeting a youth with perfect memory. This might at first seem like a great fortune, but it is in fact an awful curse. Funes can remember the exact shape of the clouds in the sky at an arbitrary time in the past, but he has trouble understanding that a dog seen from the side at 3:14 p.m. is the same dog seen from the front at 3:15 p.m. His own face in the mirror surprises him every time he sees it. Funes can’t generalize; to him, two things are the same only if they look the same down to every last detail. An unrestricted rule learner is like Funes and is equally unable to function. Learning is forgetting the details as much as it is remembering the important parts. Computers are the ultimate idiot savants: they can remember everything with no trouble at all, but that’s not what we want them to do.

The problem is not limited to memorizing instances wholesale. Whenever a learner finds a pattern in the data that is not actually true in the real world, we say that it has overfit the data. Overfitting is the central problem in machine learning. More papers have been written about it than about any other topic. Every powerful learner, whether symbolist, connectionist, or any other, has to worry about hallucinating patterns. The only safe way to avoid it is to severely restrict what the learner can learn, for example by requiring that it be a short conjunctive concept. Unfortunately, that throws out the baby with the bathwater, leaving the learner unable to see most of the true patterns that are visible in the data. Thus a good learner is forever walking the narrow path between blindness and hallucination.

Humans are not immune to overfitting, either. You could even say that it’s the root cause of a lot of our evils. Consider the little white girl who, upon seeing a Latina baby at the mall, blurted out “Look, Mom, a baby maid!” (True event.) It’s not that she’s a natural-born bigot. Rather, she overgeneralized from the few Latina maids she has seen in her short life. The world is full of Latinas with other occupations, but she hasn’t met them yet. Our beliefs are based on our experience, which gives us a very incomplete picture of the world, and it’s easy to jump to false conclusions. Being smart and knowledgeable doesn’t immunize you against overfitting, either. Aristotle overfit when he said that it takes a force to keep an object moving. Galileo’s genius was to intuit that undisturbed objects keep moving without having visited outer space to witness it firsthand.

Learning algorithms are particularly prone to overfitting, though, because they have an almost unlimited capacity to find patterns in data. In the time it takes a human to find one pattern, a computer can find millions. In machine learning, the computer’s greatest strength-its ability to process vast amounts of data and endlessly repeat the same steps without tiring-is also its Achilles’ heel. And it’s amazing what you can find if you search enough. The Bible Code, a 1998 bestseller, claimed that the Bible contains predictions of future events that you can find by skipping letters at regular intervals and assembling words from the letters you land on. Unfortunately, there are so many ways to do this that you’re guaranteed to find “predictions” in any sufficiently long text. Skeptics replied by finding them in Moby Dick and Supreme Court rulings, along with mentions of Roswell and UFOs in Genesis. John von Neumann, one of the founding fathers of computer science, famously said that “with four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” Today we routinely learn models with millions of parameters, enough to give each elephant in the world his own distinctive wiggle. It’s even been said that data mining means “torturing the data until it confesses.”

Overfitting is seriously exacerbated by noise. Noise in machine learning just means errors in the data, or random events that you can’t predict. Suppose that your friend really does like to go clubbing when there’s nothing interesting on TV, but you misremembered occasion number 3 and wrote down that there was something good on TV that night. If you now try to come up with a set of rules that makes an exception for that night, you’ll probably wind up with a worse answer than if you’d just ignored it. Or suppose that your friend had a hangover from going out the previous night and said no when ordinarily she would have said yes. Unless you know about the hangover, learning a set of rules that gets this example right is actually counterproductive: you’re better off “misclassifying” it as a no. It gets worse: noise can make it impossible to come up with any consistent set of rules. Notice that occasions 2 and 3 are in fact indistinguishable: they have exactly the same attributes. If your friend said yes on occasion 2 and no on occasion 3, there’s no rule that will get them both right.

Overfitting happens when you have too many hypotheses and not enough data to tell them apart. The bad news is that even for the simple conjunctive learner, the number of hypotheses grows exponentially with the number of attributes. Exponential growth is a scary thing. An E. coli bacterium can divide into two roughly every fifteen minutes; given enough nutrients it can grow into a mass of bacteria the size of Earth in about a day. When the number of things an algorithm needs to do grows exponentially with the size of its input, computer scientists call it a combinatorial explosion and run for cover. In machine learning, the number of possible instances of a concept is an exponential function of the number of attributes: if the attributes are Boolean, each new attribute doubles the number of possible instances by taking each previous instance and extending it with a yes or no for that attribute. In turn, the number of possible concepts is an exponential function of the number of possible instances: since a concept labels each instance as positive or negative, adding an instance doubles the number of possible concepts. As a result, the number of concepts is an exponential function of an exponential function of the number of attributes! In other words, machine learning is a combinatorial explosion of combinatorial explosions. Perhaps we should just give up and not waste our time on such a hopeless problem?

Fortunately, something happens in learning that kills off one of the exponentials, leaving only an “ordinary” singly exponential intractable problem. Suppose you have a bag full of concept definitions, each written on a piece of paper, and you take out a random one and see how well it matches the data. A bad definition is no more likely to get, say, all thousand examples in your data right than a coin is likely to come up heads a thousand times in a row. “A chair has four legs and is red or has a seat but no legs” will probably match some but not all chairs you’ve seen and also match some but not all other things. So if a random definition correctly matches a thousand examples, then it’s extremely unlikely to be the wrong definition, or at least it’s pretty close to the real one. And if the definition agrees with a million examples, then it’s practically certain to be the right one. How else would it get all those examples right?

Of course, a real learning algorithm doesn’t just take one random definition from the bag; it tries a whole bunch of them, and they’re not chosen at random. The more definitions it tries, the more likely one of them will match all the examples just by chance. If you do a million runs of a thousand coin flips, it’s practically certain that at least one run will come up all heads, and a million is a fairly small number of hypotheses to consider. For example, that’s roughly the number of possible conjunctive concepts if examples have only thirteen attributes. (Notice you don’t need to explicitly try the concepts one by one; if the best one you found using the conjunctive learner matches all the examples, the effect is the same.)

Bottom line: learning is a race between the amount of data you have and the number of hypotheses you consider. More data exponentially reduces the number of hypotheses that survive, but if you start with a lot of them, you may still have some bad ones left at the end. As a rule of thumb, if the learner only considers an exponential number of hypotheses (for example, all possible conjunctive concepts), then the data’s exponential payoff cancels it and you’re OK, provided you have plenty of examples and not too many attributes. On the other hand, if it considers a doubly exponential number (for example, all possible rule sets), then the data cancels only one of the exponentials and you’re still in trouble. You can even figure out in advance how many examples you’ll need to be pretty sure that the learner’s chosen hypothesis is very close to the true one, provided it fits all the data; in other words, for the hypothesis to be probably approximately correct. Harvard’s Leslie Valiant received the Turing Award, the Nobel Prize of computer science, for inventing this type of analysis, which he describes in his book entitled, appropriately enough, Probably Approximately Correct.

Accuracy you can believe in

In practice, Valiant-style analysis tends to be very pessimistic and to call for more data than you have. So how do you decide whether to believe what a learner tells you? Simple: you don’t believe anything until you’ve verified it on data that the learner didn’t see. If the patterns the learner hypothesized also hold true on new data, you can be pretty confident that they’re real. Otherwise you know the learner overfit. This is just the scientific method applied to machine learning: it’s not enough for a new theory to explain past evidence because it’s easy to concoct a theory that does that; the theory must also make new predictions, and you only accept it after they’ve been experimentally verified. (And even then only provisionally, because future evidence could still falsify it.)

Einstein’s general relativity was only widely accepted once Arthur Eddington empirically confirmed its prediction that the sun bends the light of distant stars. But you don’t need to wait around for new data to arrive to decide whether you can trust your learner. Rather, you take the data you have and randomly divide it into a training set, which you give to the learner, and a test set, which you hide from it and use to verify its accuracy. Accuracy on held-out data is the gold standard in machine learning. You can write a paper about a great new learning algorithm you’ve invented, but if your algorithm is not significantly more accurate than previous ones on held-out data, the paper is not publishable.

Accuracy on previously unseen data is a pretty stringent test; so much so, in fact, that a lot of science fails it. That does not make it useless, because science is not just about prediction; it’s also about explanation and understanding. But ultimately, if your models don’t make accurate predictions on new data, you can’t be sure you’ve truly understood or explained the underlying phenomena. And for machine learning, testing on unseen data is indispensable because it’s the only way to tell whether the learner has overfit or not.

Even test-set accuracy is not foolproof. According to legend, in an early military application a simple learner detected tanks with 100 percent accuracy in both the training set and the test set, each consisting of one hundred images. Amazing-or suspicious? Turns out all the tank images were lighter than the nontank ones, and that’s all the learner was picking up. These days we have larger data sets, but the quality of data collection isn’t necessarily better, so caveat emptor. Hard-nosed empirical evaluation played an important role in the growth of machine learning from a fledgling field into a mature one. Up to the late 1980s, researchers in each tribe mostly believed their own rhetoric, assumed their paradigm was fundamentally better, and communicated little with the other camps. Then symbolists like Ray Mooney and Jude Shavlik started to systematically compare the different algorithms on the same data sets and-surprise, surprise-no clear winner emerged. Today the rivalry continues, but there is much more cross-pollination. Having a common experimental framework and a large repository of data sets maintained by the machine-learning group at the University of California, Irvine, did wonders for progress. And as we’ll see, our best hope of creating a universal learner lies in synthesizing ideas from different paradigms.

Of course, it’s not enough to be able to tell when you’re overfitting; we need to avoid it in the first place. That means stopping short of perfectly fitting the data even if we’re able to. One method is to use statistical significance tests to make sure the patterns we’re seeing are really there. For example, a rule covering three hundred positive examples versus one hundred negatives and a rule covering three positives versus one negative are both 75 percent accurate on the training data, but the first rule is almost certainly better than coin flipping, while the second isn’t, since four flips of an unbiased coin could easily result in three heads. When constructing a rule, if at some point we can’t find any conditions that significantly improve its accuracy then we just stop, even if it still covers some negative examples. This reduces the rule’s training-set accuracy, but probably makes it a more accurate generalization, which is what we really care about.

We’re not home free yet, though. If I try one rule and it’s 75 percent accurate on four hundred examples, I can probably believe it. But if I try a million rules and the best one is 75 percent accurate on four hundred examples, I probably can’t, because that could easily happen by chance. This is the same problem you have when picking a mutual fund. The Clairvoyant Fund just beat the market ten years in a row. Wow, the manager must be a genius. Or not? If you have a thousand funds to choose from, the odds are better than even that one will beat the market ten years in a row, even if they’re all secretly run by dart-throwing monkeys. The scientific literature is also plagued by this problem. Significance tests are the gold standard for deciding whether a research result is publishable, but if several teams look for an effect and only one finds it, chances are it didn’t, even though you’d never guess that from reading their solid-looking paper. One solution would be to also publish negative results, so you’d know about all those failed attempts, but that hasn’t caught on. In machine learning, we can keep track of how many rules we’ve tried and adjust our significance tests accordingly, but then they tend to throw out a lot of good rules along with the bad ones. A better method is to realize that some false hypotheses will inevitably get through, but keep their number under control by rejecting enough low-significance ones, and then test the surviving hypotheses on further data.

Another popular method is to prefer simpler hypotheses. The “divide and conquer” algorithm implicitly prefers simpler rules because it stops adding conditions to a rule as soon as it covers only positive examples and stops adding rules as soon as all positive examples are covered. But to combat overfitting, we need a stronger preference for simpler rules, one that will cause us to stop adding conditions even before all negative examples have been covered. For example, we can subtract a penalty proportional to the length of the rule from its accuracy and use that as an evaluation measure.

The preference for simpler hypotheses is popularly known as Occam’s razor, but in a machine-learning context this is somewhat misleading. “Entities should not be multiplied beyond necessity,” as the razor is often paraphrased, just means choosing the simplest theory that fits the data. Occam would probably have been perplexed by the notion that we should prefer a theory that does not perfectly account for the evidence on the grounds that it will generalize better. Simple theories are preferable because they incur a lower cognitive cost (for us) and a lower computational cost (for our algorithms), not because we necessarily expect them to be more accurate. On the contrary, even our most elaborate models are usually oversimplifications of reality. Even among theories that perfectly fit the data, we know from the “no free lunch” theorem that there’s no guarantee that the simplest one will generalize best, and in fact some of the best learning algorithms-like boosting and support vector machines-learn what appear to be gratuitously complex models. (We’ll see why they work in Chapters 7 and 9.)

If your learner’s test-set accuracy disappoints, you need to diagnose the problem. Was it blindness or hallucination? In machine learning, the technical terms for these are bias and variance. A clock that’s always an hour late has high bias but low variance. If instead the clock alternates erratically between fast and slow but on average tells the right time, it has high variance but low bias. Suppose you’re down at the pub with some friends, drinking and playing darts. Unbeknownst to them, you’ve been practicing for years, and you’re a master of the game. All your darts go straight to the bull’s-eye. You have low bias and low variance, which is shown in the bottom left corner of this diagram:

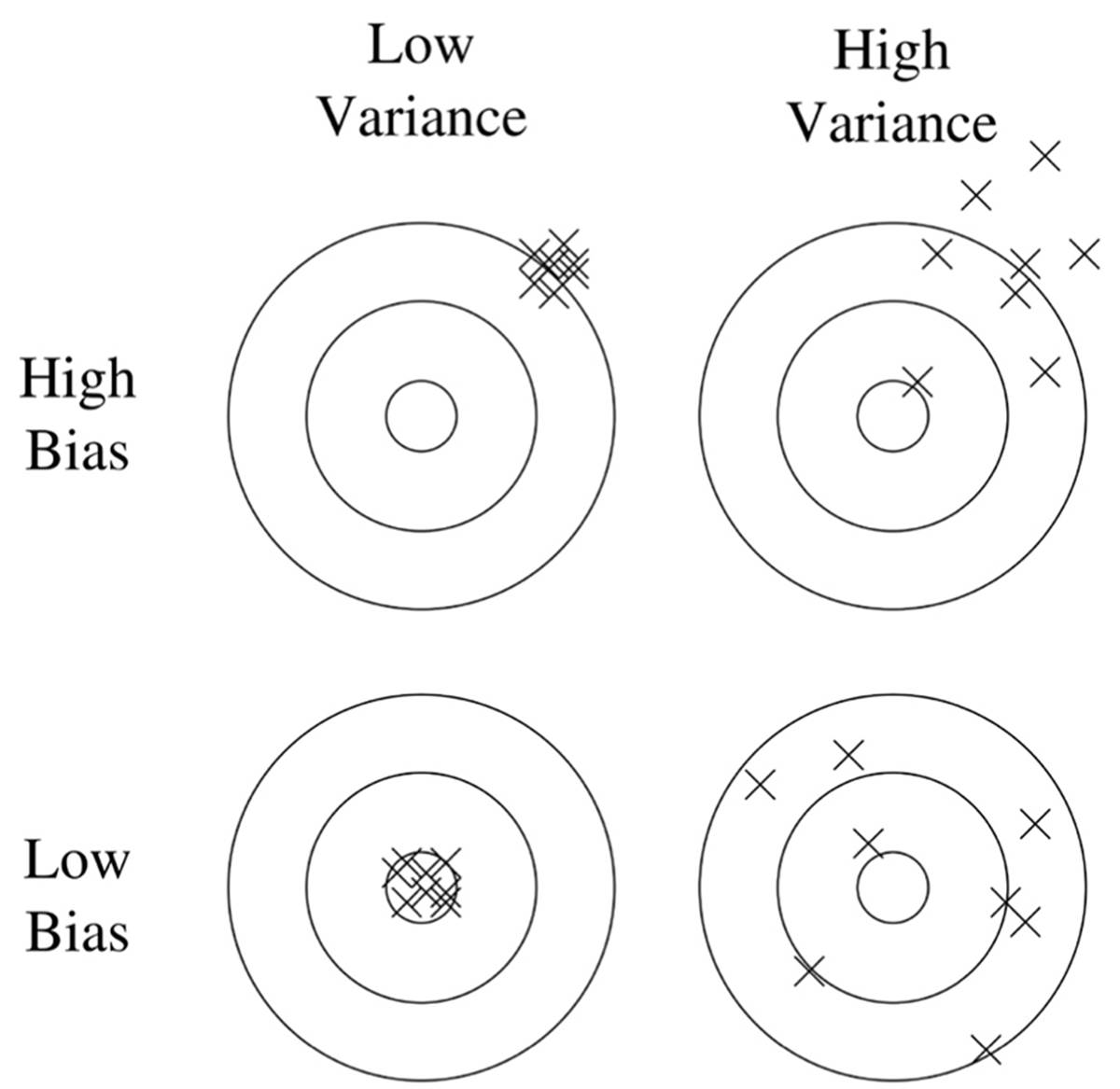
Your friend Ben is also pretty good, but he’s had a bit too much to drink. His darts are all over, but he loudly points out that on average he’s hitting the bull’s-eye. (Maybe he should have been a statistician.) This is the low-bias, high-variance case, shown in the bottom right corner. Ben’s girlfriend, Ashley, is very steady, but she has a tendency to aim too high and to the right. She has low variance and high bias (top left corner). Cody, who’s visiting from out of town and has never played darts before, is both all over and off center. He has both high bias and high variance (top right).

You can estimate the bias and variance of a learner by comparing its predictions after learning on random variations of the training set. If it keeps making the same mistakes, the problem is bias, and you need a more flexible learner (or just a different one). If there’s no pattern to the mistakes, the problem is variance, and you want to either try a less flexible learner or get more data. Most learners have a knob you can turn to make them more or less flexible, such as the threshold for significance tests or the penalty on the size of the model. Tweaking that knob is your first resort.

Induction is the inverse of deduction

The deeper problem, however, is that most learners start out knowing too little, and no amount of knob-twiddling will get them to the finish line. Without the guidance of an adult brain’s worth of knowledge, they can easily go astray. Even though it’s what most learners do, just assuming you know the form of the truth (for example, that it’s a small set of rules) is not much to hang your hat on. A strict empiricist would say that that’s all a newborn has, encoded in her brain’s architecture, and indeed children overfit more than adults do, but we would like to learn faster than a child does. (Eighteen years is a long time, and that’s not counting college.) The Master Algorithm should be able to start with a large body of knowledge, whether it was provided by humans or learned in previous runs, and use it to guide new generalizations from data. That’s what scientists do, and it’s as far as it gets from a blank slate. The “divide and conquer” rule induction algorithm can’t do it, but there’s another way to learn rules that can.

The key is to realize that induction is just the inverse of deduction, in the same way that subtraction is the inverse of addition, or integration the inverse of differentiation. This idea was first proposed by William Stanley Jevons in the late 1800s. Steve Muggleton and Wray Buntine, an English Australian team, designed the first practical algorithm based on it in 1988. The strategy of taking a well-known operation and figuring out its inverse has a storied history in mathematics. Applying it to addition led to the invention of the integers, because without negative numbers, addition doesn’t always have an inverse (3 – 4 = -1). Similarly, applying it to multiplication led to the rationals, and applying it to squaring led to complex numbers. Let’s see if we can apply it to deduction. A classic example of deductive reasoning is:

Socrates is human.

All humans are mortal.

Therefore…?…

The first statement is a fact about Socrates, and the second is a general rule about humans. What follows? That Socrates is mortal, of course, by applying the rule to Socrates. In inductive reasoning we start instead with the initial and derived facts, and look for a rule that would allow us to infer the latter from the former:

Socrates is human.

…?…

Therefore Socrates is mortal.

One such rule is: If Socrates is human, then he’s mortal. This does the job, but is not very useful because it’s specific to Socrates. But now we apply Newton’s principle and generalize the rule to all entities: If an entity is human, then it’s mortal. Or, more succinctly: All humans are mortal. Of course, it would be rash to induce this rule from Socrates alone, but we know similar facts about other humans:

Plato is human. Plato is mortal.

Aristotle is human. Aristotle is mortal.

And so on.

For each pair of facts, we construct the rule that allows us to infer the second fact from the first one and generalize it by Newton’s principle. When the same general rule is induced over and over again, we can have some confidence that it’s true.

So far we haven’t done anything that the “divide and conquer” algorithm couldn’t do. Suppose, however, that instead of knowing that Socrates, Plato, and Aristotle are human, we just know that they’re philosophers. We still want to conclude that they’re mortal, and we have previously induced or been told that all humans are mortal. What’s missing now? A different rule: All philosophers are human. This also a valid generalization (at least until we solve AI and robots start philosophizing), and it “fills the hole” in our reasoning:

Socrates is a philosopher.

All philosophers are human.

All humans are mortal.

Therefore Socrates is mortal.

We can also induce rules purely from other rules. If we know that all philosophers are human and mortal, we can induce that all humans are mortal. (We don’t induce that all mortals are human because we know other mortal creatures, like cats and dogs. On the other hand, scientists, artists, and so on are also human and mortal, reinforcing the rule.) In general, the more rules and facts we start out with, the more opportunities we have to induce new rules using “inverse deduction.” And the more rules we induce, the more rules we can induce. It’s a virtuous circle of knowledge creation, limited only by overfitting risk and computational cost. But here, too, having initial knowledge helps: if instead of one large hole we have many small ones to fill, our induction steps will be less risky and therefore less likely to overfit. (For example, given the same number of examples, inducing that all philosophers are human is less risky than inducing that all humans are mortal.)

Inverting an operation is often difficult because the inverse is not unique. For example, a positive number has two square roots, one positive and one negative (2² = (-2)² = 4). Most famously, integrating the derivative of a function only recovers the function up to a constant. The derivative of a function tells us how much that function goes up or down at each point. Adding up all those changes gives us the function back, except we don’t know where it started; we can “slide” the integrated function up or down without changing the derivative. To make life easy, we can “clamp down” the function by assuming the additive constant is zero. Inverse deduction has a similar problem, and Newton’s principle is one solution. For example, from All Greek philosophers are human and All Greek philosophers are mortal we can induce that All humans are mortal, or just that All Greeks are mortal. But why settle for the more modest generalization? Instead, we can assume that all humans are mortal until we meet an exception. (Which, according to Ray Kurzweil, will be soon.)

In the meantime, one important application of inverse deduction is predicting whether new drugs will have harmful side effects. Failure during animal testing and clinical trials is the main reason new drugs take many years and billions of dollars to develop. By generalizing from known toxic molecular structures, we can form rules that quickly weed out many apparently promising compounds, greatly increasing the chances of successful trials on the remaining ones.

Learning to cure cancer

More generally, inverse deduction is a great way to discover new knowledge in biology, and doing that is the first step in curing cancer. According to the Central Dogma, everything that happens in a living cell is ultimately controlled by its genes, via the proteins whose synthesis they initiate. In effect, a cell is like a tiny computer, and DNA is the program running on it: change the DNA, and a skin cell can become a neuron or a mouse cell can turn into a human one. In a computer program, all bugs are the programmer’s fault. But in a cell, bugs can arise spontaneously, when radiation or a copying error changes a gene into a different one, a gene is accidentally copied twice, and so on. Most of the time these mutations cause the cell to die silently, but sometimes the cell starts to grow and divide uncontrollably and a cancer is born.

Curing cancer means stopping the bad cells from reproducing without harming the good ones. That requires knowing how they differ, and in particular how their genomes differ, since all else follows from that. Luckily, gene sequencing is becoming routine and affordable. Using it, we can learn to predict which drugs will work against which cancer genes. This contrasts with traditional chemotherapy, which affects all cells indiscriminately. Learning which drugs work against which mutations requires a database of patients, their cancers’ genomes, the drugs tried, and the outcomes. The simplest rules encode one-to-one correspondences between genes and drugs, such as If the BCR-ABL gene is present, then use Gleevec. (BCR-ABL causes a type of leukemia, and Gleevec cures it in nine out of ten patients.) Once sequencing cancer genomes and collating treatment outcomes becomes standard practice, many more rules like this will be discovered.

That’s only the beginning, however. Most cancers involve a combination of mutations, or can only be cured by drugs that haven’t been discovered yet. The next step is to learn rules with more complex conditions, involving the cancer’s genome, the patient’s genome and medical history, known side effects of drugs, and so on. But ultimately what we need is a model of how the entire cell works, enabling us to simulate on the computer the effect of a specific patient’s mutations, as well as the effect of different combinations of drugs, existing or speculative. Our main sources of information for building such models are DNA sequencers, gene expression microarrays, and the biological literature. Combining these is where inverse deduction can shine.

Adam, the robot scientist we met in Chapter 1, gives a preview. Adam’s goal is to figure out how yeast cells work. It starts with basic knowledge of yeast genetics and metabolism and a trove of gene expression data from yeast cells. It then uses inverse deduction to hypothesize which genes are expressed as which proteins, designs microarray experiments to test them, revises its hypotheses, and repeats. Whether each gene is expressed depends on other genes and conditions in the environment, and the resulting web of interactions can be represented as a set of rules, such as:

If the temperature is high, gene A is expressed.

If gene A is expressed and gene B is not, gene C is expressed.

If gene C is expressed, gene D is not.

If we knew the first and third rules but not the second, and we had microarray data where at a high temperature B and D were not expressed, we could induce the second rule by inverse deduction. Once we have that rule, and perhaps have verified it using a microarray experiment, we can use it as the basis for further inductive inferences. In a similar manner, we can piece together the sequences of chemical reactions by which proteins do their work.

Just knowing which genes regulate which genes and how proteins organize the cell’s web of chemical reactions is not enough, though. We also need to know how much of each molecular species is produced. DNA microarrays and other experiments can provide this type of quantitative information, but inverse deduction, with its “all or none” logical character, is not very good at dealing with it. For that we need the connectionist methods that we’ll meet in the next chapter.

A game of twenty questions

Another limitation of inverse deduction is that it’s very computationally intensive, which makes it hard to scale to massive data sets. For these, the symbolist algorithm of choice is decision tree induction. Decision trees can be viewed as an answer to the question of what to do if rules of more than one concept match an instance. How do we then decide which concept the instance belongs to? If we see a partly occluded object with a flat surface and four legs, how do we decide whether it is a table or a chair? One option is to order the rules, for example by decreasing accuracy, and choose the first one that matches. Another is to let the rules vote. Decision trees instead ensure a priori that each instance will be matched by exactly one rule. This will be the case if each pair of rules differs in at least one attribute test, and such a rule set can be organized into a decision tree. For example, consider these rules:

If you’re for cutting taxes and pro-life, you’re a Republican.

If you’re against cutting taxes, you’re a Democrat.

If you’re for cutting taxes, pro-choice, and against gun control, you’re an independent.

If you’re for cutting taxes, pro-choice, and pro-gun control, you’re a Democrat.

These can be organized into the following decision tree:

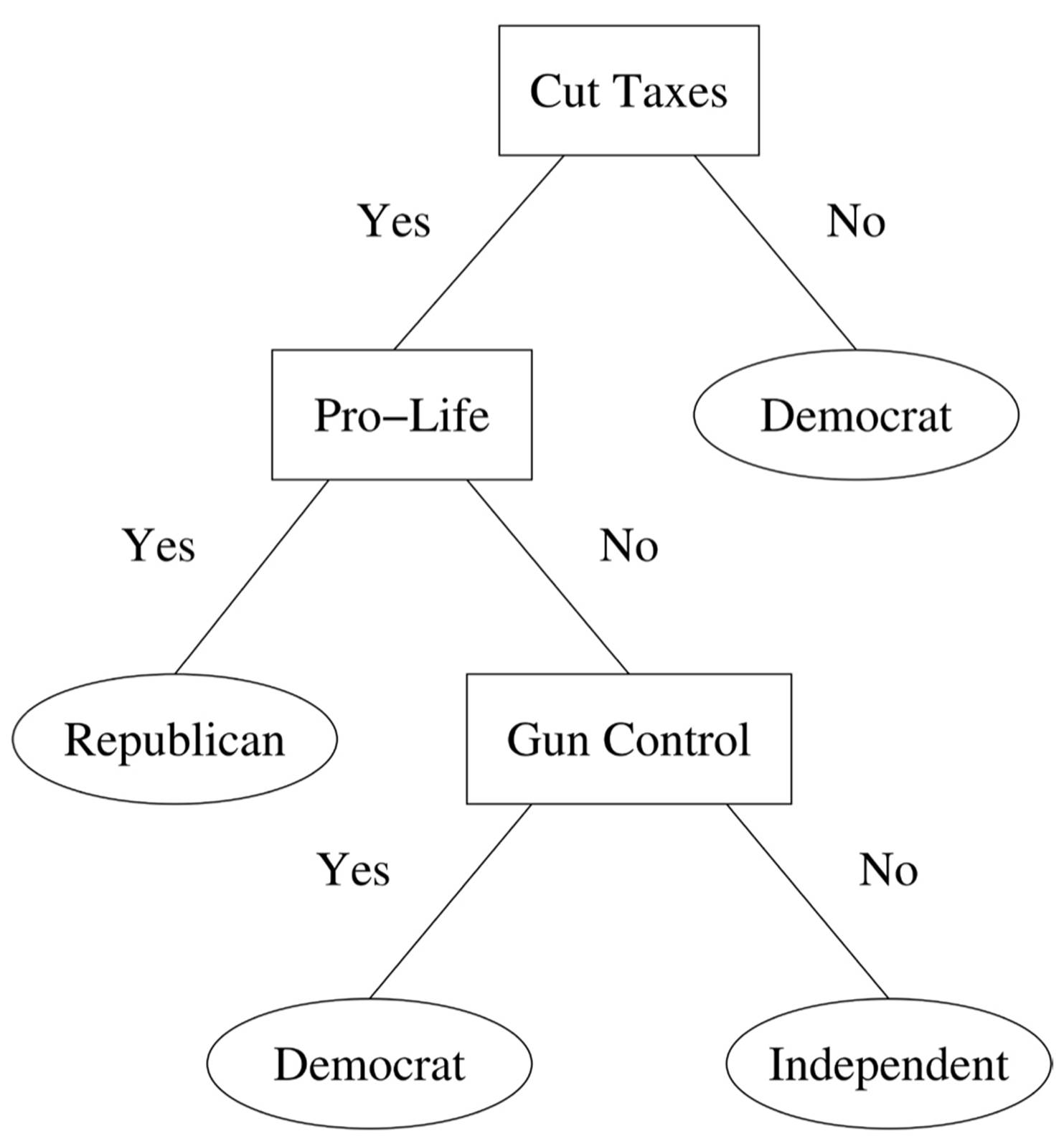
A decision tree is like playing a game of twenty questions with an instance. Starting at the root, each node asks about the value of one attribute, and depending on the answer, we follow one or another branch. When we arrive at a leaf, we read off the predicted concept. Each path from the root to a leaf corresponds to a rule. If this reminds you of those annoying phone menus you have to get through when you call customer service, it’s not an accident: a phone menu is a decision tree. The computer on the other end of the line is playing a game of twenty questions with you to figure out what you want, and each menu is a question.

According to the decision tree above, you’re either a Republican, a Democrat, or an independent; you can’t be more than one, or none of the above. Sets of concepts with this property are called sets of classes, and the algorithm that predicts them is a classifier. A single concept implicitly defines two classes: the concept itself and its negation. (For example, spam and nonspam.) Classifiers are the most widespread form of machine learning.

We can learn decision trees using a variant of the “divide and conquer” algorithm. First we pick an attribute to test at the root. Then we focus on the examples that went down each branch and pick the next test for those. (For example, we check whether tax-cutters are pro-life or pro-choice.) We repeat this for each new node we induce until all the examples in a branch have the same class, at which point we label that branch with the class.

One salient question is how to pick the best attribute to test at a node. Accuracy-the number of correctly predicted examples-doesn’t work very well, because we’re not trying to predict a particular class; rather, we’re trying to gradually separate the classes until each branch is “pure.” This brings to mind the concept of entropy from information theory. The entropy of a set of objects is a measure of the amount of disorder in it. If a group of 150 people includes 50 Republicans, 50 Democrats, and 50 independents, its political entropy is maximum. On the other hand, if they’re all Republican then the entropy is zero (as far as party affiliation goes). So to learn a good decision tree, we pick at each node the attribute that on average yields the lowest class entropy across all its branches, weighted by how many examples go into each branch.

As with rule learning, we don’t want to induce a tree that perfectly predicts the classes of all the training examples, because it would probably overfit. As before, we can use significance tests or a penalty on the size of the tree to prevent this.

Having a branch for each value of an attribute is fine if the attribute is discrete, but what about numeric attributes? If we had a branch for every value of a continuous variable, the tree would be infinitely wide. A simple solution is to pick a few key thresholds by entropy and use those. For example, is the patient’s temperature above or below 100 degrees Fahrenheit? That, combined with other symptoms, may be all the doctor needs to know about the patient’s temperature to decide if he has an infection.

Decision trees are used in many different fields. In machine learning, they grew out of work in psychology. Earl Hunt and colleagues used them in the 1960s to model how humans acquire new concepts, and one of Hunt’s graduate students, J. Ross Quinlan, later tried using them for chess. His original goal was to predict the outcome of king-rook versus king-knight endgames from the board positions. From those humble beginnings, decision trees have grown to be, according to surveys, the most widely used machine-learning algorithm. It’s not hard to see why: they’re easy to understand, fast to learn, and usually quite accurate without too much tweaking. Quinlan is the most prominent researcher in the symbolist school. An unflappable, down-to-earth Australian, he made decision trees the gold standard in classification by dint of relentlessly improving them year after year, and writing beautifully clear papers about them.

Whatever you want to predict, there’s a good chance someone has used a decision tree for it. Microsoft’s Kinect uses decision trees to figure out where various parts of your body are from the output of its depth camera; it can then use their motions to control the Xbox game console. In a 2002 head-to-head competition, decision trees correctly predicted three out of every four Supreme Court rulings, while a panel of experts got less than 60 percent correct. Thousands of decision tree users can’t be wrong, you think, and sketch one to predict your friend’s reply when you ask her out:

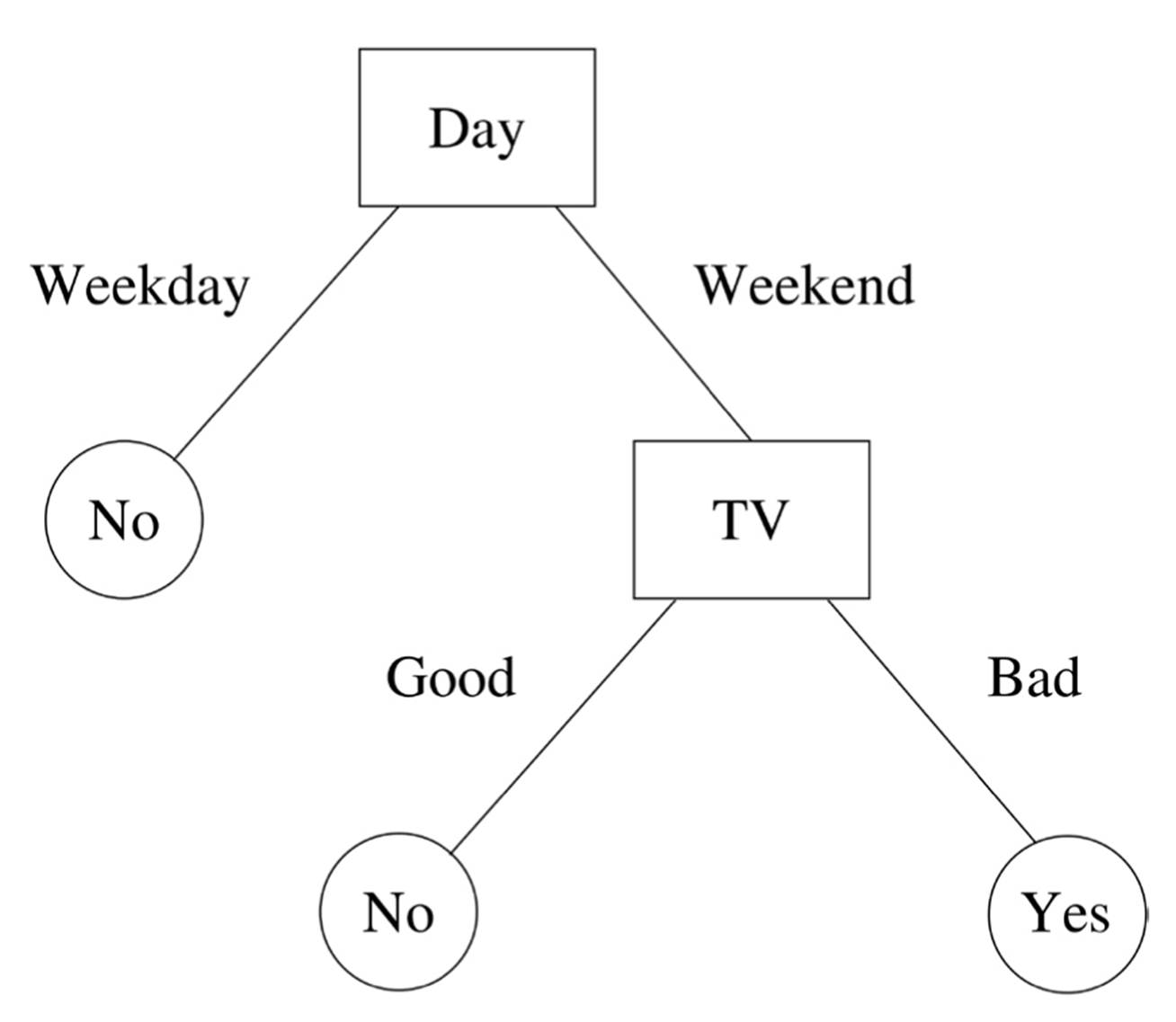
According to this tree, tonight she’ll say yes. With a deep breath, you pick up the phone and dial her number.

The symbolists

The symbolists’ core belief is that all intelligence can be reduced to manipulating symbols. A mathematician solves equations by moving symbols around and replacing symbols by other symbols according to predefined rules. The same is true of a logician carrying out deductions. According to this hypothesis, intelligence is independent of the substrate; it doesn’t matter if the symbol manipulations are done by writing on a blackboard, switching transistors on and off, firing neurons, or playing with Tinkertoys. If you have a setup with the power of a universal Turing machine, you can do anything. Software can be cleanly separated from hardware, and if your concern is figuring out how machines can learn, you (thankfully) don’t need to worry about the latter beyond buying a PC or cycles on Amazon’s cloud.

Symbolist machine learners share this belief in the power of symbol manipulation with many other computer scientists, psychologists, and philosophers. The psychologist David Marr argued that every information processing system should be studied at three distinct levels: the fundamental properties of the problem it’s solving; the algorithms and representations used to solve it; and how they are physically implemented. For example, addition can be defined by a set of axioms irrespective of how it’s carried out; numbers can be expressed in different ways (e.g., Roman and Arabic) and added using different algorithms; and these can be implemented using an abacus, a pocket calculator, or even, very inefficiently, in your head. Learning is a prime example of a cognitive faculty we can profitably study according to Marr’s levels.

Symbolist machine learning is an offshoot of the knowledge engineering school of AI. In the 1970s, so-called knowledge-based systems scored some impressive successes, and in the 1980s they spread rapidly, but then they died out. The main reason they did was the infamous knowledge acquisition bottleneck: extracting knowledge from experts and encoding it as rules is just too difficult, labor-intensive, and failure-prone to be viable for most problems. Letting the computer automatically learn to, say, diagnose diseases by looking at databases of past patients’ symptoms and the corresponding outcomes turned out to be much easier than endlessly interviewing doctors. Suddenly, the work of pioneers like Ryszard Michalski, Tom Mitchell, and Ross Quinlan had a new relevance, and the field hasn’t stopped growing since. (Another important problem was that knowledge-based systems had trouble dealing with uncertainty, of which more in Chapter 6.)

Because of its origins and guiding principles, symbolist machine learning is still closer to the rest of AI than the other schools. If computer science were a continent, symbolist learning would share a long border with knowledge engineering. Knowledge is traded in both directions-manually entered knowledge for use in learners, induced knowledge for addition to knowledge bases-but at the end of the day the rationalist-empiricist fault line runs right down that border, and crossing it is not easy.

Symbolism is the shortest path to the Master Algorithm. It doesn’t require us to figure out how evolution or the brain works, and it avoids the mathematical complexities of Bayesianism. Sets of rules and decision trees are easy to understand, so we know what the learner is up to. This makes it easier to figure out what it’s doing right and wrong, fix the latter, and have confidence in the results.

Despite the popularity of decision trees, inverse deduction is the better starting point for the Master Algorithm. It has the crucial property that incorporating knowledge into it is easy-and we know Hume’s problem makes that essential. Also, sets of rules are an exponentially more compact way to represent most concepts than decision trees. Converting a decision tree to a set of rules is easy: each path from the root to a leaf becomes a rule, and there’s no blowup. On the other hand, in the worst case converting a set of rules into a decision tree requires converting each rule into a mini-decision tree, and then replacing each leaf of rule 1’s tree with a copy of rule 2’s tree, each leaf of each copy of rule 2 with a copy of rule 3, and so on, causing a massive blowup.

Inverse deduction is like having a superscientist systematically looking at the evidence, considering possible inductions, collating the strongest, and using those along with other evidence to construct yet further hypotheses-all at the speed of computers. It’s clean and beautiful, at least for the symbolist taste. On the other hand, it has some serious shortcomings. The number of possible inductions is vast, and unless we stay close to our initial knowledge, it’s easy to get lost in space. Inverse deduction is easily confused by noise: how do we figure out what the missing deductive steps are, if the premises or conclusions are themselves wrong? Most seriously, real concepts can seldom be concisely defined by a set of rules. They’re not black and white: there’s a large gray area between, say, spam and nonspam. They require weighing and accumulating weak evidence until a clear picture emerges. Diagnosing an illness involves giving more weight to some symptoms than others, and being OK with incomplete evidence. No one has ever succeeded in learning a set of rules that will recognize a cat by looking at the pixels in an image, and probably no one ever will.

Connectionists, in particular, are highly critical of symbolist learning. According to them, concepts you can define with logical rules are only the tip of the iceberg; there’s a lot going on under the surface that formal reasoning just can’t see, in the same way that most of what goes on in our minds is subconscious. You can’t just build a disembodied automated scientist and hope he’ll do something meaningful-you have to first endow him with something like a real brain, connected to real senses, growing up in the world, perhaps even stubbing his toe every now and then. And how do you build such a brain? By reverse engineering the competition. If you want to reverse engineer a car, you look under the hood. If you want to reverse engineer the brain, you look inside the skull.

Оглавление книги