Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER SIX: In the Church of the Reverend Bayes

CHAPTER SIX: In the Church of the Reverend Bayes

The dark hulk of the cathedral rises from the night. Light pours from its stained-glass windows, projecting intricate equations onto the streets and buildings beyond. As you approach, you can hear chanting inside. It seems to be Latin, or perhaps math, but the Babel fish in your ear translates it into English: “Turn the crank! Turn the crank!” Just as you enter, the chant dissolves into an “Aaaah!” of satisfaction, and a murmur of “The posterior! The posterior!” You peek through the crowd. A massive stone tablet towers above the altar with a formula engraved on it in ten-foot letters:

P ( A|B ) = P ( A ) P(B|A) / P(B)

As you stare uncomprehendingly at it, your Google Glass helpfully flashes: “Bayes’ theorem.” Now the crowd starts to chant “More data! More data!” A stream of sacrificial victims is being inexorably pushed toward the altar. Suddenly, you realize that you’re in the middle of it-too late. As the crank looms over you, you scream, “No! I don’t want to be a data point! Let me gooooo!”

You wake up in a cold sweat. Lying on your lap is a book entitled The Master Algorithm. Shaking off the nightmare, you resume reading where you had left off.

The theorem that runs the world

The path to optimal learning begins with a formula that many people have heard of: Bayes’ theorem. But here we’ll see it in a whole new light and realize that it’s vastly more powerful than you’d guess from its everyday uses. At heart, Bayes’ theorem is just a simple rule for updating your degree of belief in a hypothesis when you receive new evidence: if the evidence is consistent with the hypothesis, the probability of the hypothesis goes up; if not, it goes down. For example, if you test positive for AIDS, your probability of having it goes up. Things get more interesting when you have many pieces of evidence, such as the results of multiple tests. To combine them all without suffering a combinatorial explosion, we need to make simplifying assumptions. Things get even more interesting when we consider many hypotheses at once, such as all the different possible diagnoses for a patient. Computing the probability of each disease from the patient’s symptoms in a reasonable amount of time can take a lot of smarts. Once we know how to do all these things, we’ll be ready to learn the Bayesian way. For Bayesians, learning is “just” another application of Bayes’ theorem, with whole models as the hypotheses and the data as the evidence: as you see more data, some models become more likely and some less, until ideally one model stands out as the clear winner. Bayesians have invented fiendishly clever kinds of models. So let’s get started.

Thomas Bayes was an eighteenth-century English clergyman who, without realizing it, became the center of a new religion. You may well ask how that could happen, until you notice that it happened to Jesus, too: Christianity as we know it was invented by Saint Paul, while Jesus saw himself as the pinnacle of the Jewish faith. Similarly, Bayesianism as we know it was invented by Pierre-Simon de Laplace, a Frenchman who was born five decades after Bayes. Bayes was the preacher who first described a new way to think about chance, but it was Laplace who codified those insights into the theorem that bears Bayes’s name.

One of the greatest mathematicians of all time, Laplace is perhaps best known for his dream of Newtonian determinism:

An intelligence that, at a given instant, could comprehend all the forces by which nature is animated and the respective situation of the beings that make it up, if moreover it were vast enough to submit these data to analysis, would encompass in the same formula the movements of the greatest bodies of the universe and those of the lightest atoms. For such an intelligence nothing would be uncertain, and the future, like the past, would be open to its eyes.

This is ironic, since Laplace was also the father of probability theory, which he believed was just common sense reduced to calculation. At the heart of his explorations in probability was a preoccupation with Hume’s question. For example, how do we know the sun will rise tomorrow? It has done so every day until today, but that’s no guarantee it will continue. Laplace’s answer had two parts. The first is what we now call the principle of indifference, or principle of insufficient reason. We wake up one day-at the beginning of time, let’s say, which for Laplace was five thousand years or so ago-and after a beautiful afternoon, we see the sun go down. Will it come back? We’ve never seen the sun rise, and there is no particular reason to believe it will or won’t. Therefore we should consider the two scenarios equally likely and say that the sun will rise again with a probability of one-half. But, Laplace went on, if the past is any guide to the future, every day that the sun rises should increase our confidence that it will continue to do so. After five thousand years, the probability that the sun will rise yet again tomorrow should be very close to one, but not quite there, since we can never be completely certain. From this thought experiment, Laplace derived his so-called rule of succession, which estimates the probability that the sun will rise again after having risen n times as (n + 1) / (n + 2). When n = 0, this is just ?; and as n increases, so does the probability, approaching 1 when n approaches infinity.

This rule arises from a more general principle. Suppose you awake in the middle of the night on a strange planet. Even though all you can see is the starry sky, you have reason to believe that the sun will rise at some point, since most planets revolve around themselves and their sun. So your estimate of the corresponding probability should be greater than one-half (two-thirds, say). We call this the prior probability that the sun will rise, since it’s prior to seeing any evidence. It’s not based on counting the number of times the sun has risen on this planet in the past, because you weren’t there to see it; rather, it reflects your a priori beliefs about what will happen, based on your general knowledge of the universe. But now the stars start to fade, so your confidence that the sun does rise on this planet goes up, based on your experience on Earth. Your confidence is now a posterior probability, since it’s after seeing some evidence. The sky begins to lighten, and the posterior probability takes another leap. Finally, a sliver of the sun’s bright disk appears above the horizon and perhaps catches “the Sultan’s turret in a noose of light,” as in the opening verse of the Rubaiyat. Unless you’re hallucinating, it is now certain that the sun will rise.

The crucial question is exactly how the posterior probability should evolve as you see more evidence. The answer is Bayes’ theorem. We can think of it in terms of cause and effect. Sunrise causes the stars to fade and the sky to lighten, but the latter is stronger evidence of daybreak, since the stars could fade in the middle of the night due to, say, fog rolling in. So the probability of sunrise should increase more after seeing the sky lighten than after seeing the stars fade. In mathematical notation, we say that P(sunrise | lightening-sky), the conditional probability of sunrise given that the sky is lightening, is greater than P(sunrise | fading-stars), its conditional probability given that the stars are fading. According to Bayes’ theorem, the more likely the effect is given the cause, the more likely the cause is given the effect: if P(lightening-sky | sunrise) is higher than P(fading-stars | sunrise), perhaps because some planets are far enough from their sun that the stars still shine after sunrise, then P(sunrise | lightening sky) is also higher than P(sunrise | fading-stars).

This is not the whole story, however. If we observe an effect that would happen even without the cause, then surely that’s not much evidence of the cause being present. Bayes’ theorem incorporates this by saying that P(cause | effect) goes down with P(effect), the prior probability of the effect (i.e., its probability in the absence of any knowledge of the causes). Finally, other things being equal, the more likely a cause is a priori, the more likely it should be a posteriori. Putting all of these together, Bayes’ theorem says that

P(cause | effect) = P(cause) ? P(effect | cause) / P(effect).

Replace cause by A and effect by B and omit the multiplication sign for brevity, and you get the ten-foot formula in the cathedral.

That’s just a statement of the theorem, not a proof, of course. But the proof is surprisingly simple. We can illustrate it with an example from medical diagnosis, one of the “killer apps” of Bayesian inference. Suppose you’re a doctor, and you’ve diagnosed a hundred patients in the last month. Fourteen of them had the flu, twenty had a fever, and eleven had both. The conditional probability of fever given flu is therefore eleven out of fourteen, or 11/14. Conditioning reduces the size of the universe that we’re considering, in this case from all patients to only patients with the flu. In the universe of all patients, the probability of fever is 20/100; in the universe of flu-stricken patients, it’s 11/14. The probability that a patient has the flu and a fever is the fraction of patients that have the flu times the fraction of those that have a fever: P(flu, fever) = P(flu) ? P(fever | flu) = 14/100 ? 11/14 = 11/100. But we could equally well have done this the other way around: P(flu, fever) = P(fever) ? P(flu | fever). Therefore, since they’re both equal to P(flu,fever), P(fever) ? P(flu | fever) = P(flu) ? P(fever | flu). Divide both sides by P(fever), and you get P(flu | fever) = P(flu) ? P(fever | flu) / P(fever). That’s it! That’s Bayes’ theorem, with flu as the cause and fever as the effect.

Humans, it turns out, are not very good at Bayesian inference, at least when verbal reasoning is involved. The problem is that we tend to neglect the cause’s prior probability. If you test positive for HIV, and the test only gives 1 percent false positives, should you panic? At first sight, it seems like your chances of having AIDS are now 99 percent. Yikes! But let’s keep a cool head and apply Bayes’ theorem step-by-step: P(HIV | positive) = P(HIV) ? P(positive | HIV) / P(positive). P(HIV) is the prevalence of HIV in the general population, which is about 0.3 percent in the United States. P(positive) is the probability that the test comes out positive whether or not you have AIDS; let’s say that’s 1 percent. So P(HIV | positive) = 0.003 ? 0.99 / 0.01 = 0.297. That’s very different from 0.99! The reason is that HIV is rare in the general population. The test coming out positive increases your chances of having AIDS by two orders of magnitude, but they’re still less than half. If you test positive for HIV, the right thing to do is to stay calm and take another, more definitive test. Chances are you’ll be fine.

Bayes’ theorem is useful because what we usually know is the probability of the effects given the causes, but what we want to know is the probability of the causes given the effects. For example, we know what percentage of flu patients have a fever, but what we really want to know is how likely a patient with a fever is to have the flu. Bayes’ theorem lets us go from one to the other. Its significance extends far beyond that, however. For Bayesians, this innocent-looking formula is the F = ma of machine learning, the foundation from which a vast number of results and applications flow. And whatever the Master Algorithm is, it must be “just” a computational implementation of Bayes’ theorem. I put just in quotes because implementing Bayes’ theorem on a computer turns out to be fiendishly hard for all but the simplest problems, for reasons that we’re about to see.

Bayes’ theorem as a foundation for statistics and machine learning is bedeviled not just by computational difficulty but also by extreme controversy. You might be forgiven for wondering why: Isn’t it a straightforward consequence of the notion of conditional probability, as we saw in the flu example? Indeed, no one has a problem with the formula itself. The controversy is in how Bayesians obtain the probabilities that go into it and what those probabilities mean. For most statisticians, the only legitimate way to estimate probabilities is by counting how often the corresponding events occur. For example, the probability of fever is 0.2 because twenty out of one hundred observed patients had it. This is the “frequentist” interpretation of probability, and the dominant school of thought in statistics takes its name from it. But notice that in the sunrise example, and in Laplace’s principle of indifference, we did something different: we pulled a probability out of thin air. What exactly justifies assuming a priori that the probability the sun will rise is one-half, or two-thirds, or whatever? Bayesians’ answer is that a probability is not a frequency but a subjective degree of belief. Therefore it’s up to you what you make it, and all that Bayesian inference lets you do is update your prior beliefs with new evidence to obtain your posterior beliefs (also known as “turning the Bayesian crank”). Bayesians’ devotion to this idea is near religious, enough to withstand two hundred years of attacks and counting. And with the appearance on the stage of computers powerful enough to do Bayesian inference, and the massive data sets to go with it, they’re beginning to gain the upper hand.

All models are wrong, but some are useful

In reality, a doctor doesn’t diagnose the flu just based on whether you have a fever; she takes a whole bunch of symptoms into account, including whether you have a cough, a sore throat, a runny nose, a headache, chills, and so on. So what we really need to compute is P(flu | fever, cough, sore throat, runny nose, headache, chills,… ). By Bayes’ theorem, we know that this is proportional to P(fever, cough, sore throat, runny nose, headache, chills,…| flu). But now we run into a problem. How are we supposed to estimate this probability? If each symptom is a Boolean variable (you either have it or you don’t) and the doctor takes n symptoms into account, a patient could have 2n possible combinations of symptoms. If we have, say, twenty symptoms and a database of ten thousand patients, we’ve only seen a small fraction of the roughly one million possible combinations. Worse still, to accurately estimate the probability of a particular combination, we need at least tens of observations of it, meaning the database would need to include tens of millions of patients. Add another ten symptoms, and we’d need more patients than there are people on Earth. With a hundred symptoms, even if we were somehow able to magically get the data, there wouldn’t be enough space on all the hard disks in the world to store all the probabilities. And if a patient walks in with a combination of symptoms we haven’t seen before, we won’t know how to diagnose him. We’re face-to-face with our old foe: the combinatorial explosion.

Therefore we do what we always have to do in life: compromise. We make simplifying assumptions that whittle the number of probabilities we have to estimate down to something manageable. A very simple and popular assumption is that all the effects are independent given the cause. This means that, for example, having a fever doesn’t change how likely you are to also have a cough, if we already know you have the flu. Mathematically, this is saying that P(fever, cough | flu) is just P(fever | flu) ? P(cough | flu). Lo and behold: each of these is easy to estimate from a small number of observations. In fact, we did it for fever in the previous section, and it would be no different for cough or any other symptom. The number of observations we need no longer goes up exponentially with the number of symptoms; in fact, it doesn’t go up at all.

Notice that we’re only saying that fever and cough are independent given that you have the flu, not overall. Clearly, if we don’t know whether you have the flu, fever and cough are highly correlated, since you’re much more likely to have a cough if you already have a fever. P(fever, cough) is not equal to P(fever) ? P(cough). All we’re saying is that, if we know you have the flu, knowing whether you have a fever gives us no additional information about whether you have a cough. Likewise, if you don’t know the sun is about to rise and you see the stars fade, your expectation that the sky will lighten increases; but if you already know that sunrise is imminent, seeing the stars fade makes no difference.

Notice also that it’s only thanks to Bayes’ theorem that we were able to pull off this trick. If we wanted to directly estimate P(flu | fever, cough, etc.), without first turning it into P(fever, cough, etc. | flu) using the theorem, we’d still need an exponential number of probabilities, one for each combination of symptoms and flu/not flu.

A learner that uses Bayes’ theorem and assumes the effects are independent given the cause is called a Na?ve Bayes classifier. That’s because, well, that’s such a na?ve assumption. In reality, having a fever makes having a cough more likely, even if you already know you have the flu, because (for example) it makes you more likely to have a bad flu. But machine learning is the art of making false assumptions and getting away with it. As the statistician George Box famously put it: “All models are wrong, but some are useful.” An oversimplified model that you have enough data to estimate is better than a perfect one that you don’t. It’s astonishing how simultaneously very wrong and very useful some models can be. The economist Milton Friedman even argued in a highly influential essay that the best theories are the most oversimplified, provided their predictions are accurate, because they explain the most with the least. That seems to me like a bridge too far, but it illustrates that, counter to Einstein’s dictum, science often progresses by making things as simple as possible, and then some.

No one is sure who invented the Na?ve Bayes algorithm. It was mentioned without attribution in a 1973 pattern recognition textbook, but it only took off in the 1990s, when researchers noticed that, surprisingly, it was often more accurate than much more sophisticated learners. I was a graduate student at the time, and when I belatedly decided to include Na?ve Bayes in my experiments, I was shocked to find it did better than all the other algorithms I was comparing, save one-luckily, the algorithm I was developing for my thesis, or I might not be here now.

Na?ve Bayes is now very widely used. For example, it forms the basis of many spam filters. It all began when David Heckerman, a prominent Bayesian researcher who is also a medical doctor, had the idea of treating spam as a disease whose symptoms are the words in the e-mail: Viagra is a symptom, and so is free, but your best friend’s first name probably signals a legit e-mail. We can then use Na?ve Bayes to classify e-mails into spam and nonspam, provided spammers generate e-mails by picking words at random. That’s a ridiculous assumption, of course: it would only be true if sentences had no syntax and no content. But that summer Mehran Sahami, then a Stanford graduate student, tried it out during an internship at Microsoft Research, and it worked great. When Bill Gates asked Heckerman how this could be, he pointed out that to identify spam you don’t need to understand the details of the message; it’s enough to get the gist of it by seeing which words it contains.

A basic search engine also uses an algorithm quite similar to Na?ve Bayes to decide which web pages to return in answer to your query. The main difference is that, instead of spam/not-spam, it’s trying to predict relevant/not-relevant. The list of prediction problems Na?ve Bayes has been applied to is practically endless. Peter Norvig, director of research at Google, told me at one point that it was the most widely used learner there, and Google uses machine learning in every nook and cranny of what it does. It’s not hard to see why Na?ve Bayes would be popular among Googlers. Surprising accuracy aside, it scales great; learning a Na?ve Bayes classifier is just a matter of counting how many times each attribute co-occurs with each class and takes barely longer than reading the data from disk.

You could even use Na?ve Bayes, tongue-in-cheek, on a much larger scale than Google’s: to model the whole universe. Indeed, if you believe in an omnipotent God, then you can model the universe as a vast Na?ve Bayes distribution where everything that happens is independent given God’s will. The catch, of course, is that we can’t read God’s mind, but in Chapter 8 we’ll investigate how to learn Na?ve Bayes models even when we don’t know the classes of the examples.

It might not seem so at first, but Na?ve Bayes is closely related to the perceptron algorithm. The perceptron adds weights and Na?ve Bayes multiplies probabilities, but if you take a logarithm, the latter reduces to the former. Both can be seen as generalizations of simple If… then… rules, where each antecedent can count more or less toward the conclusion instead of being “all or none.” This is just one example of the deeper connections among learners that hint at a Master Algorithm. You may not consciously know Bayes’ theorem (well, now you do), but in a way every one of the ten billion neurons in your brain is a tiny instance of it.

Na?ve Bayes is a good conceptual model of a learner to use when reading the press: it captures the pairwise correlation between each input and the output, which is often all that’s needed to understand references to learning algorithms in news stories. But machine learning is not just pairwise correlations, of course, any more than the brain is just one neuron. The real action begins when we look for more complex patterns.

From Eugene Onegin to Siri

In 1913, on the eve of World War I, the Russian mathematician Andrei Markov published a paper applying probability to, of all things, poetry. In it, he modeled a classic of Russian literature, Pushkin’s Eugene Onegin, using what we now call a Markov chain. Rather than assume that each letter was generated at random independently of the rest, he introduced a bare minimum of sequential structure: he let the probability of each letter depend on the letter immediately preceding it. He showed that, for example, vowels and consonants tend to alternate, so if you see a consonant, the next letter (ignoring punctuation and white space) is much more likely to be a vowel than it would be if letters were independent. This may not seem like much, but in the days before computers, it required spending hours manually counting characters, and Markov’s idea was quite new. If Vowel_i is a Boolean variable that’s true if the ith letter of Eugene Onegin is a vowel and false if it’s a consonant, we can represent Markov’s model with a chain-like graph like this, with an arrow between two nodes indicating a direct dependency between the corresponding variables:

Markov assumed (wrongly but usefully) that the probabilities are the same at every position in the text. Thus we need to estimate only three probabilities: P(Vowel₁ = True), P(Vowel_i+1 = True | Vowel_i = True), and P(Vowel_i+1= True | Vowel_i = False). (Since probabilities sum to one, from these we can immediately obtain P(Vowel₁ = False), etc.) As with Na?ve Bayes, we can have as many variables as we want without the number of probabilities we need to estimate going through the roof, but now the variables actually depend on each other.

If we measure not just the probability of vowels versus consonants, but the probability of each letter in the alphabet following each other, we can have fun generating new texts with the same statistics as Onegin: choose the first letter, then choose the second based on the first, and so on. The result is complete gibberish, of course, but if we let each letter depend on several previous letters instead of just one, it starts to sound more like the ramblings of a drunkard, locally coherent even if globally meaningless. Still not enough to pass the Turing test, but models like this are a key component of machine-translation systems, like Google Translate, which lets you see the whole web in English (or almost), regardless of the language the pages were originally written in.

PageRank, the algorithm that gave rise to Google, is itself a Markov chain. Larry Page’s idea was that web pages with many incoming links are probably more important than pages with few, and links from important pages should themselves count for more. This sets up an infinite regress, but we can handle it with a Markov chain. Imagine a web surfer going from page to page by randomly following links: the states of this Markov chain are web pages instead of characters, making it a vastly larger problem, but the math is the same. A page’s score is then the fraction of the time the surfer spends on it, or equivalently, his probability of landing on the page after wandering around for a long time.

Markov chains turn up everywhere and are one of the most intensively studied topics in mathematics, but they’re still a very limited kind of probabilistic model. We can go one step further with a model like this:

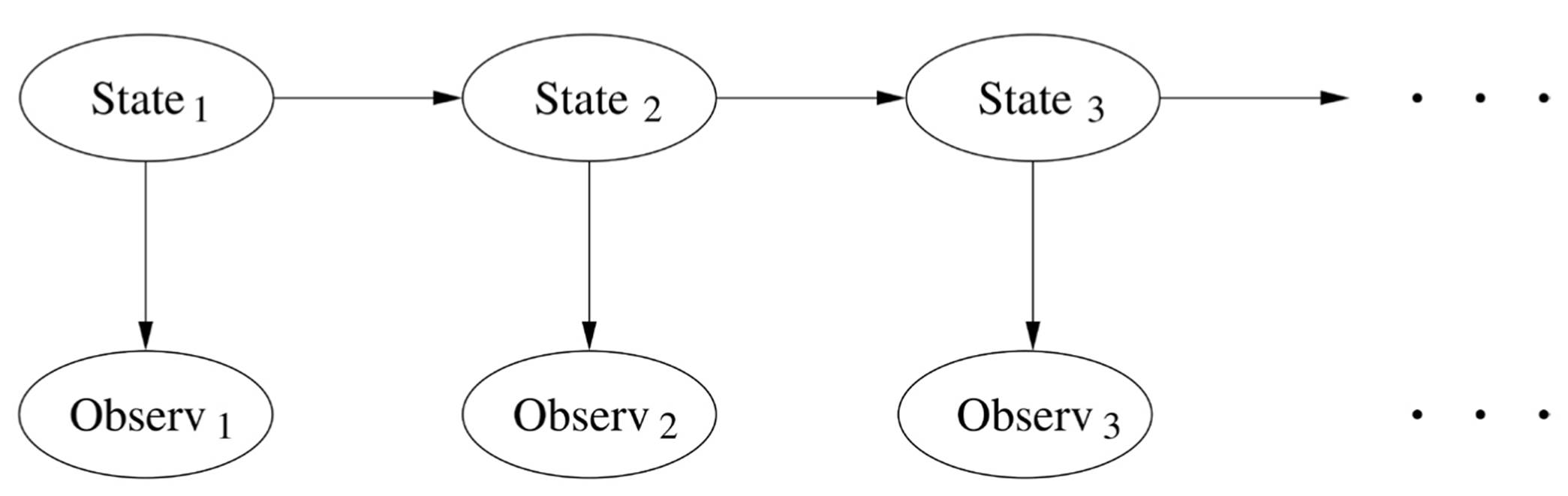
The states form a Markov chain, as before, but we don’t get to see them; we have to infer them from the observations. This is called a hidden Markov model, or HMM for short. (Slightly misleading, because it’s the states that are hidden, not the model.) HMMs are at the heart of speech-recognition systems like Siri. In speech recognition, the hidden states are written words, the observations are the sounds spoken to Siri, and the goal is to infer the words from the sounds. The model has two components: the probability of the next word given the current one, as in a Markov chain, and the probability of hearing various sounds given the word being pronounced. (How exactly to do the inference is a fascinating problem that we’ll turn to after the next section.)

Siri aside, you use an HMM every time you talk on your cell phone. That’s because your words get sent over the air as a stream of bits, and the bits get corrupted in transit. The HMM then figures out the intended bits (hidden state) from the ones received (observations), which it should be able to do as long as not too many bits got mangled.

HMMs are also a favorite tool of computational biologists. A protein is a sequence of amino acids, and DNA is a sequence of bases. If we want to predict, for example, how a protein will fold into a 3-D shape, we can treat the amino acids as the observations and the type of fold at each point as the hidden state. Similarly, we can use an HMM to identify the sites in DNA where gene transcription is initiated and many other properties.

If the states and observations are continuous variables instead of discrete ones, the HMM becomes what’s known as a Kalman filter. Economists use Kalman filters to remove noise from time series of quantities like GDP, inflation, and unemployment. The “true” GDP values are the hidden states; at each time step, the true value should be similar to the observed one, but also to the previous true value, since the economy seldom makes abrupt jumps. The Kalman filter trades off these two, yielding a smoother curve that still accords with the observations. When a missile cruises to its target, it’s a Kalman filter that keeps it on track. Without it, there would have been no man on the moon.

Everything is connected, but not directly

HMMs are good for modeling sequences of all kinds, but they’re still a far cry from the flexibility of the symbolists’ If… then… rules, where anything can appear as an antecedent, and a rule’s consequent can in turn be an antecedent in any downstream rule. If we allow such an arbitrary structure in practice, however, the number of probabilities we need to learn blows up. For a long time no one knew how to square this circle, and researchers resorted to ad-hoc schemes, like attaching confidence estimates to rules and somehow combining them. If A implies B with confidence 0.8 and B implies C with confidence 0.7, then perhaps A implies C with confidence 0.8 ? 0.7.

The problem with these schemes is that they can go badly awry. From the two perfectly reasonable rules If the sprinkler is on, then the grass is wet and If the grass is wet, then it rained, I can infer the nonsensical rule If the sprinkler is on, then it rained. A more insidious problem is that with confidence-rated rules we’re prone to double-counting evidence. Suppose you read in the New York Times that aliens have landed. Maybe it’s a prank, even though it’s not April 1. But now you see the same headline in the Wall Street Journal, USA Today, and the Washington Post. You start to panic, like the listeners to Orson Welles’s infamous War of the Worlds radio broadcast who didn’t realize it was a dramatization. If, however, you check the fine print and notice that all four newspapers got the story from the Associated Press, you go back to suspecting it’s a prank, this time by an AP reporter. Rule systems have no way of dealing with this, and neither does Na?ve Bayes. If it uses features like Reported in the New York Times as predictors that a news story is true, all it can do is add Reported by AP, which only makes things worse.

The breakthrough came in the early 1980s, when Judea Pearl, a professor of computer science at the University of California, Los Angeles, invented a new representation: Bayesian networks. Pearl is one of the most distinguished computer scientists in the world, his methods having swept through machine learning, AI, and many other fields. He won the Turing Award, the Nobel Prize of computer science, in 2012.

Pearl realized that it’s OK to have a complex network of dependencies among random variables, provided each variable depends directly on only a few others. We can represent these dependencies with a graph like the ones we saw for Markov chains and HMMs, except now the graph can have any structure (as long as the arrows don’t form closed loops). One of Pearl’s favorite examples is burglar alarms. The alarm at your house should go off if a burglar attempts to break in, but it could also be triggered by an earthquake. (In Los Angeles, where Pearl lives, earthquakes are almost as frequent as burglaries.) If you’re working late one night and your neighbor Bob calls to say he just heard your alarm go off, but your neighbor Claire doesn’t, should you call the police? Here’s the graph of dependencies:

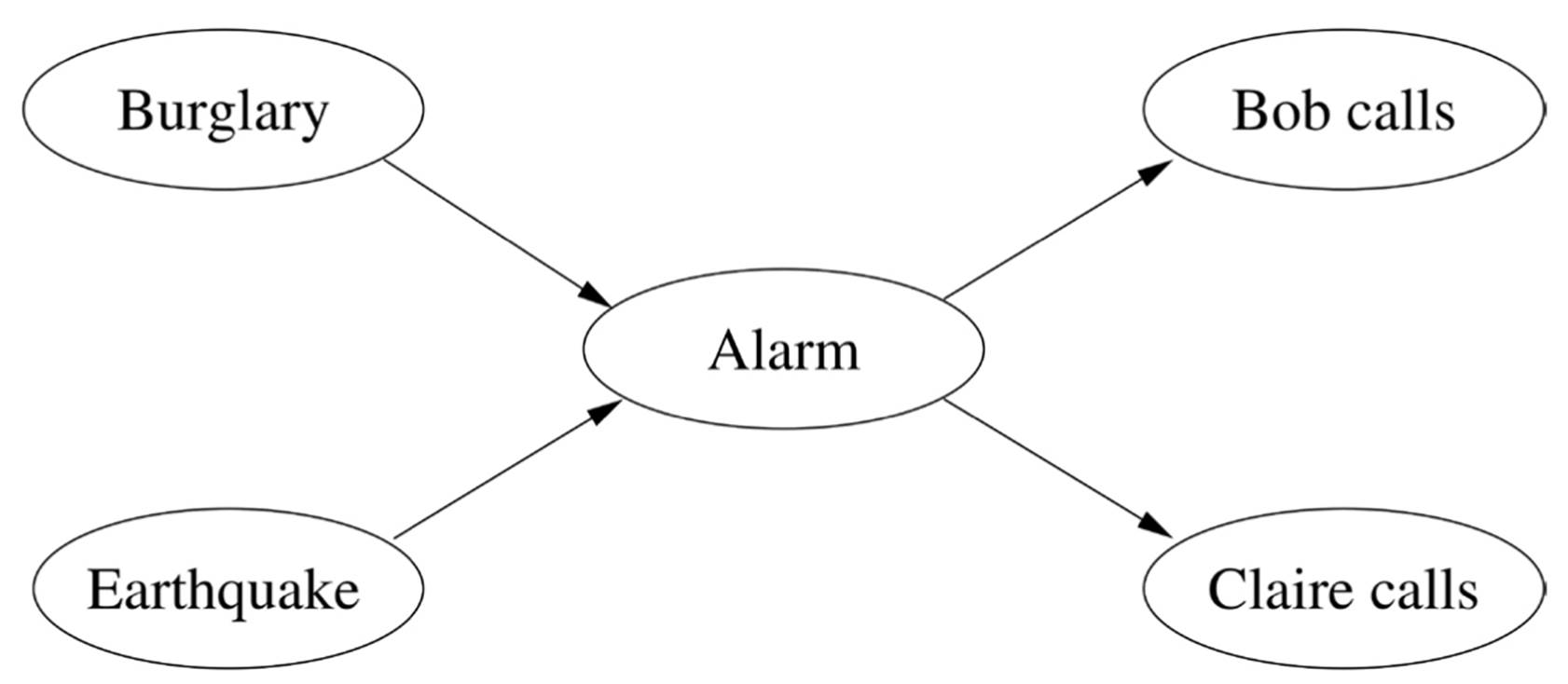
If there’s an arrow from one node to another in the graph, we say that the first node is a parent of the second. So Alarm’s parents are Burglary and Earthquake, and Alarm is the sole parent of Bob calls and Claire calls. A Bayesian network is a graph of dependencies like this, together with a table for each variable, giving its probability for each combination of values of its parents. For Burglary and Earthquake we only need one probability each, since they have no parents. For Alarm we need four: the probability that it goes off even if there’s no burglary or earthquake, the probability that it goes off if there’s a burglary and no earthquake, and so on. For Bob calls we need two probabilities (given alarm and given no alarm), and similarly for Claire.

Here’s the crucial point: Bob calling depends on Burglary and Earthquake, but only through Alarm. Bob’s call is conditionally independent of Burglary and Earthquake given Alarm, and so is Claire’s. If the alarm doesn’t go off, your neighbors sleep soundly, and the burglar proceeds undisturbed. Also, Bob and Claire are independent given Alarm. Without this independence structure, you’d need to learn 2⁵ = 32 probabilities, one for each possible state of the five variables. (Or 31, if you’re a stickler for details, since the last one can be left implicit.) With the conditional independencies, all you need is 1 + 1 + 4 + 2 + 2 = 10, a savings of 68 percent. And that’s just in this tiny example; with hundreds or thousands of variables, the savings would be very close to 100 percent.

The first law of ecology, according to biologist Barry Commoner, is that everything is connected to everything else. That may be true, but it would also make the world impossible to understand, if not for the saving grace of conditional independence: everything is connected, but only indirectly. In order to affect me, something that happens a mile away must first affect something in my neighborhood, even if only through the propagation of light. As one wag put it, space is the reason everything doesn’t happen to you. Put another way, the structure of space is an instance of conditional independence.

In the burglary example, the full table of thirty-two probabilities is never represented explicitly, but it’s implicit in the collection of smaller tables and graph structure. To obtain P(Burglary, Earthquake, Alarm, Bob calls, Claire calls), all I have to do is multiply P(Burglary), P(Earthquake), P(Alarm | Burglary, Earthquake), P(Bob calls | Alarm), and P(Claire calls | Alarm). It’s the same in any Bayesian network: to obtain the probability of a complete state, just multiply the probabilities from the corresponding lines in the individual variables’ tables. So, provided the conditional independencies hold, no information is lost by switching to the more compact representation. And in this way we can easily compute the probabilities of extremely unusual states, including states that were never observed before. Bayesian networks give the lie to the common misconception that machine learning can’t predict very rare events, or “black swans,” as Nassim Taleb calls them.

In retrospect, we can see that Na?ve Bayes, Markov chains, and HMMs are all special cases of Bayesian networks. The structure of Na?ve Bayes is:

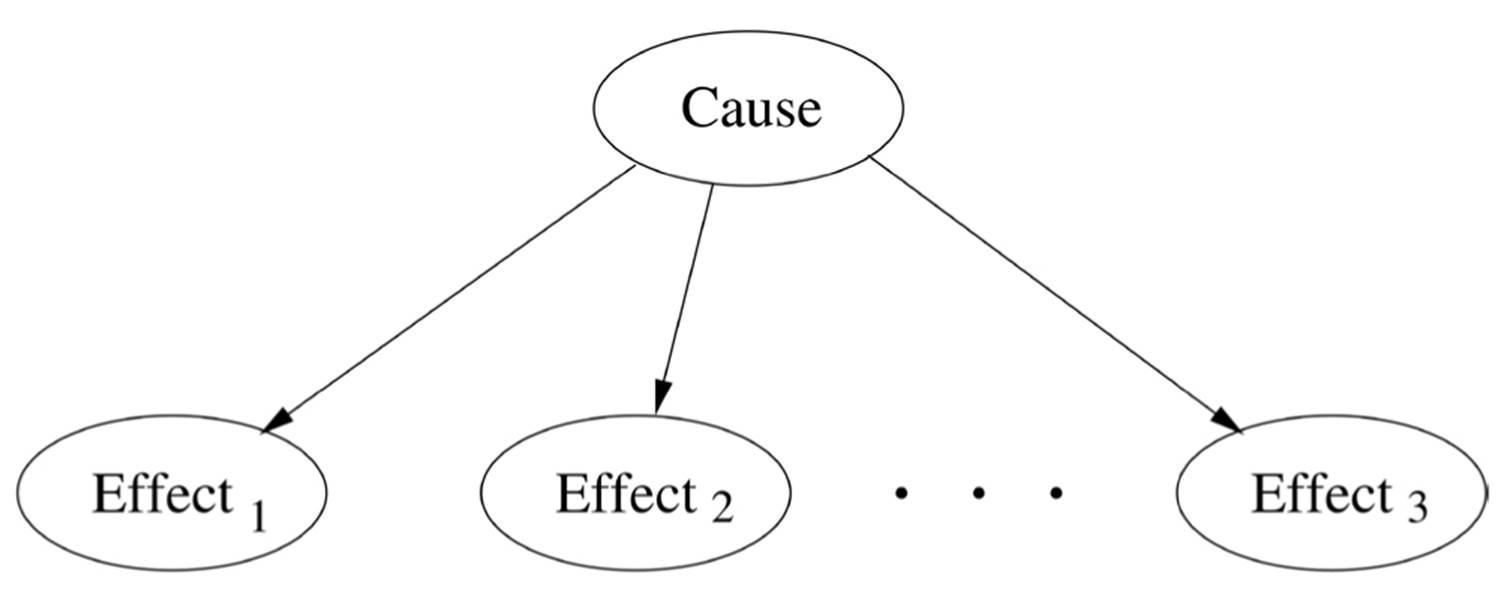
Markov chains encode the assumption that the future is conditionally independent of the past given the present. HMMs assume in addition that each observation depends only on the corresponding state. Bayesian networks are for Bayesians what logic is for symbolists: a lingua franca that allows us to elegantly encode a dizzying variety of situations and devise algorithms that work uniformly in all of them.

We can think of a Bayesian network as a “generative model,” a recipe for probabilistically generating a state of the world: first decide independently whether there’s a burglary and/or an earthquake, then based on that decide whether the alarm goes off, and then based on that whether Bob and Claire call. A Bayesian network tells a story: A happened, and it led to B; at the same time, C also happened, and B and C together caused D. To compute the probability of a particular story, we just multiply the probabilities of all of its different strands.

One of the most exciting applications of Bayesian networks is modeling how genes regulate each other in living cells. Billions of dollars have been spent trying to discover pairwise correlations between individual genes and specific diseases, but the yield has been disappointingly low. In retrospect, this is not so surprising: a cell’s behavior is the result of complex interactions among genes and the environment, and a single gene has limited predictive power. But with Bayesian networks, we can uncover these interactions, provided we have the requisite data, and with the spread of DNA microarrays, we increasingly do.

After pioneering the application of machine learning to spam filtering, David Heckerman turned to using Bayesian networks in the fight against AIDS. The AIDS virus is a tough adversary because it mutates rapidly, making it difficult for any one vaccine or drug to pin it down for long. Heckerman noticed that this is the same cat-and-mouse game that spam filters play with spam and decided to apply a lesson he had learned there: attack the weakest link. In the case of spam, weak links include the URLs you have to use to take payment from the customer. In the case of HIV, they’re small regions of the virus protein that can’t change without hurting the virus. If he could train the immune system to recognize these regions and attack the cells displaying them, he just might have an AIDS vaccine. Heckerman and coworkers used a Bayesian network to help identify the vulnerable regions and developed a vaccine delivery mechanism that could teach the immune system to attack just those regions. The delivery mechanism worked in mice, and clinical trials are now in preparation.

It often happens that, even after we take all conditional independences into account, some nodes in a Bayesian network still have too many parents. Some networks are so dense with arrows that when we print them, the page turns solid black. (The physicist Mark Newman calls them “ridiculograms.”) A doctor needs to simultaneously diagnose all the possible diseases a patient could have, not just one, and every disease is a parent of many different symptoms. A fever could be caused by any number of conditions besides the flu, but it’s hopeless to try to predict its probability given every possible combination of conditions. All is not lost. Instead of a table specifying the node’s conditional probability for every state of its parents, we can learn a simpler distribution. The most popular choice is a probabilistic version of the logical OR operation: any cause alone can provoke a fever, but each cause has a certain probability of failing to do so, even if it’s usually sufficient. Heckerman and others have learned Bayesian networks that diagnose hundreds of infectious diseases in this way. Google uses a giant Bayesian network of this type in its AdSense system for automatically choosing ads to place on web pages. The network relates a million content variables to each other and to twelve million words and phrases via over three hundred million arrows, all learned from a hundred billion text snippets and search queries.

On a lighter note, Microsoft’s Xbox Live uses a Bayesian network to rate players and match players of similar skill. The outcome of a game is a probabilistic function of the opponents’ skill levels, and using Bayes’ theorem we can infer a player’s skill from the outcomes of his games.

The inference problem

There’s a big snag in all of this, unfortunately. Just because a Bayesian network lets us compactly represent a probability distribution doesn’t mean we can also reason efficiently with it. Suppose you want to compute P(Burglary | Bob called, Claire didn’t). By Bayes’ theorem, you know this is just P(Burglary) P(Bob called, Claire didn’t | Burglary) / P(Bob called, Claire didn’t), or equivalently, P(Burglary, Bob called, Claire didn’t) / P(Bob called, Claire didn’t). If you had the full table with the probabilities of all states, you could obtain both of these probabilities by adding up the corresponding lines in the table. For example, P(Bob called, Claire didn’t) is the sum of the probabilities of all the lines where Bob calls and Claire doesn’t. But the Bayesian network doesn’t give you the full table. You could always construct it from the individual tables, but that takes exponential time and space. What we really want is to compute P(Burglary | Bob called, Claire didn’t) without building the full table. That, in a nutshell, is the problem of inference in Bayesian networks.

In many cases we can do this and avoid the exponential blowup. Suppose you’re leading a platoon in single file through enemy territory in the dead of night, and you want to make sure that all your soldiers are still with you. You could stop and count them yourself, but that wastes too much time. A cleverer solution is to just ask the first soldier behind you: “How many soldiers are behind you?” Each soldier asks the next the same question, until the last one says “None.” The next-to-last soldier can now say “One,” and so on all the way back to the first soldier, with each soldier adding one to the number of soldiers behind him. Now you know how many soldiers are still with you, and you didn’t even have to stop.

Siri uses the same idea to compute the probability that you just said, “Call the police” from the sounds it picked up from the microphone. Think of “Call the police” as a platoon of words marching across the page in single file. Police wants to know its probability, but for that it needs to know the probability of the; and the in turn needs to know the probability of call. So call computes its probability and passes it on to the, which does the same and passes the result to police. Now police knows its probability, duly influenced by every word in the sentence, but we never had to construct the full table of eight possibilities (the first word is call or isn’t, the second is the or isn’t, and the third is police or isn’t). In reality, Siri considers all words that could appear in each position, not just whether the first word is call or not and so on, but the algorithm is the same. Perhaps Siri thinks, based on the sounds, that the first word was either call or tell, the second was the or her, and the third was police or please. Individually, perhaps the most likely words are call, the, and please. But that forms the nonsensical sentence “Call the please,” so taking the other words into account, Siri concludes that the sentence is really “Call the police.” It makes the call, and with luck the police get to your house in time to catch the burglar.

The same idea still works if the graph is a tree instead of a chain. If instead of a platoon you’re in command of a whole army, you can ask each of your company commanders how many soldiers are behind him and add up their answers. Each company commander in turn asks each of his platoon commanders, and so on. But if the graph forms loops, you’re in trouble. If there’s a liaison officer who’s a member of two platoons, he gets counted twice; in fact, everyone behind him gets counted twice. This is what happens in the “aliens have landed” scenario, if you want to compute, say, the probability of panic:

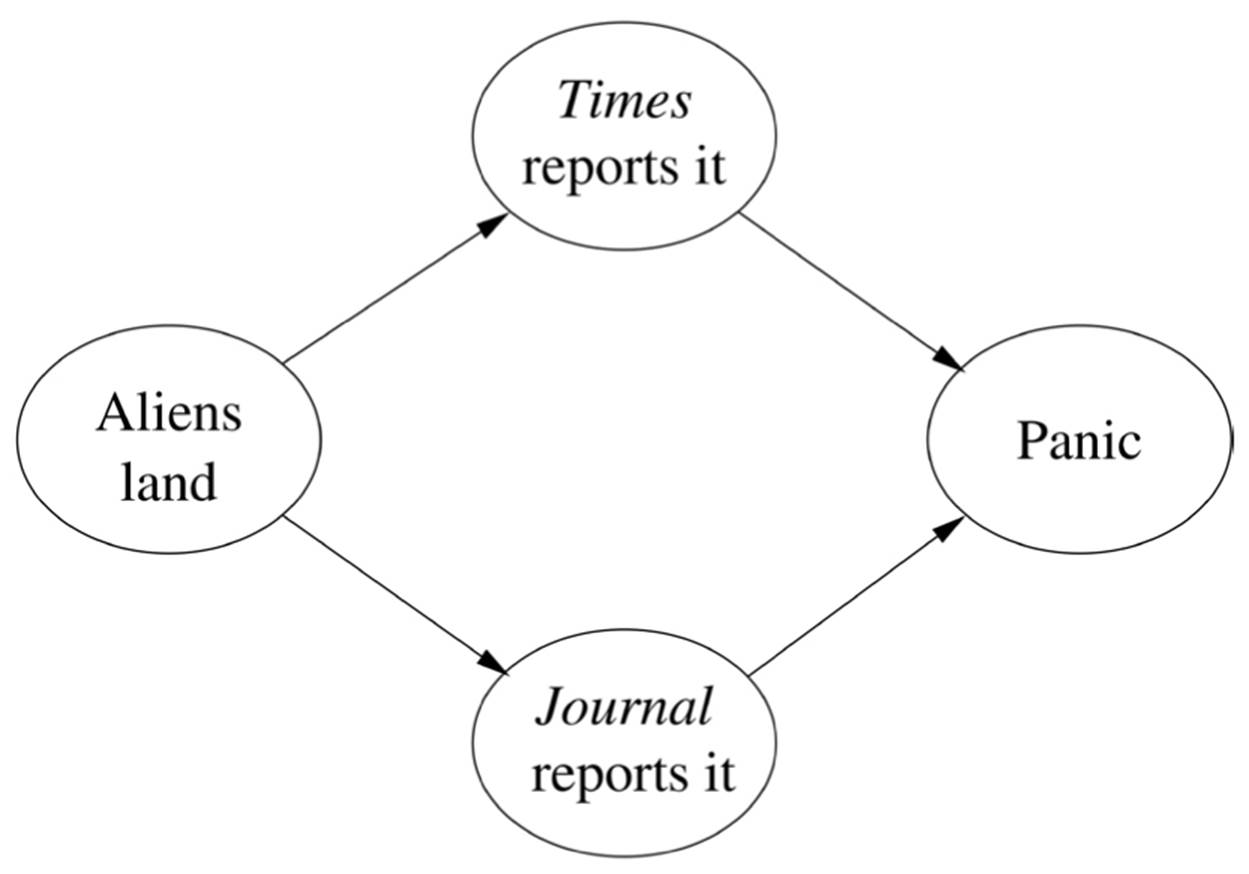
One solution is to combine The Times reports it and The Journal reports it into a single megavariable with four values: YesYes if they both do, YesNo if the Times reports a landing and the Journal doesn’t, and so on. This turns the graph into a chain of three variables, and all is well. However, every time you add a news source, the number of values of the megavariable doubles. If instead of two news sources you have fifty, the megavariable has 2⁵⁰ values. So this method can only get you so far, and no other known method does any better.

The problem is worse than it seems, because Bayesian networks in effect have “invisible” arrows to go along with the visible ones. Burglary and Earthquake are a priori independent, but the alarm going off entangles them: the alarm makes you suspect a burglary, but if now you hear on the radio that there’s been an earthquake, you assume that’s what caused the alarm. The earthquake has explained away the alarm, making a burglary less likely, and the two are therefore dependent. In a Bayesian network, all parents of the same variable are interdependent in this way, and this in turn introduces further dependencies, making the resulting graph often much denser than the original one.

The crucial question for inference is whether you can make the filled-in graph “look like a tree” without the trunk getting too thick. If the megavariable in the trunk has too many possible values, the tree grows out of control until it covers the whole planet, like the baobabs in The Little Prince. In the tree of life, each species is a branch, but inside each branch is a graph, with each creature having two parents, four grandparents, some number of offspring, and so on. The “thickness” of a branch is the size of the species’ population. When the branches are too thick, our only choice is to resort to approximate inference.

One solution, left as an exercise by Pearl in his book on Bayesian networks, is to pretend the graph has no loops and just keep propagating probabilities back and forth until they converge. This is known as loopy belief propagation, both because it works on graphs with loops and because it’s a crazy idea. Surprisingly, it turns out to work quite well in many cases. For instance, it’s a state-of-the art method for wireless communication, with the random variables being the bits in the message, encoded in a clever way. But loopy belief propagation can also converge to the wrong answers or oscillate forever. Another solution, which originated in physics but was imported into machine learning and greatly extended by Michael Jordan and others, is to approximate an intractable distribution with a tractable one and optimize the latter’s parameters to make it as close as possible to the former.

The most popular option, however, is to drown our sorrows in alcohol, get punch drunk, and stumble around all night. The technical term for this is Markov chain Monte Carlo, or MCMC for short. The “Monte Carlo” part is because the method involves chance, like a visit to the eponymous casino, and the “Markov chain” part is because it involves taking a sequence of steps, each of which depends only on the previous one. The idea in MCMC is to do a random walk, like the proverbial drunkard, jumping from state to state of the network in such a way that, in the long run, the number of times each state is visited is proportional to its probability. We can then estimate the probability of a burglary, say, as the fraction of times we visited a state where there was a burglary. A “well-behaved” Markov chain converges to a stable distribution, so after a while it always gives approximately the same answers. For example, when you shuffle a deck of cards, after a while all card orders are equally likely, no matter the initial order; so you know that if there are n possible orders, the probability of each one is 1/n. The trick in MCMC is to design a Markov chain that converges to the distribution of our Bayesian network. One easy option is to repeatedly cycle through the variables, sampling each one according to its conditional probability given the state of its neighbors. People often talk about MCMC as a kind of simulation, but it’s not: the Markov chain does not simulate any real process; rather, we concocted it to efficiently generate samples from a Bayesian network, which is itself not a sequential model.

The origins of MCMC go all the way back to the Manhattan Project, when physicists needed to estimate the probability that neutrons would collide with atoms and set off a chain reaction. But in more recent decades, it has sparked such a revolution that it’s often considered one of the most important algorithms of all time. MCMC is good not just for computing probabilities but for integrating any function. Without it, scientists were limited to functions they could integrate analytically, or to well-behaved, low-dimensional integrals they could approximate as a series of trapezoids. With MCMC, they’re free to build complex models, knowing the computer will do the heavy lifting. Bayesians, for one, probably have MCMC to thank for the rising popularity of their methods more than anything else.

On the downside, MCMC is often excruciatingly slow to converge, or fools you by looking like it’s converged when it hasn’t. Real probability distributions are usually very peaked, with vast wastelands of minuscule probability punctuated by sudden Everests. The Markov chain then converges to the nearest peak and stays there, leading to very biased probability estimates. It’s as if the drunkard followed the scent of alcohol to the nearest tavern and stayed there all night, instead of wandering all around the city like we wanted him to. On the other hand, if instead of using a Markov chain we just generated independent samples, like simpler Monte Carlo methods do, we’d have no scent to follow and probably wouldn’t even find that first tavern; it would be like throwing darts at a map of the city, hoping they land smack dab on the pubs.

Inference in Bayesian networks is not limited to computing probabilities. It also includes finding the most probable explanation for the evidence, such as the disease that best explains the symptoms or the words that best explain the sounds Siri heard. This is not the same as just picking the most probable word at each step, because words that are individually likely given their sounds may be unlikely to occur together, as in the “Call the please” example. However, similar kinds of algorithms also work for this task (and they are, in fact, what most speech recognizers use). Most importantly, inference includes making the best decisions, guided not just by the probabilities of different outcomes but also by the corresponding costs (or utilities, to use the technical term). The cost of ignoring an e-mail from your boss asking you to do something by tomorrow is much greater than the cost of seeing a piece of spam, so often it’s better to let an e-mail through even if it does seem fairly likely to be spam.

Driverless cars and other robots are a prime example of probabilistic inference in action. As the car drives around, it simultaneously builds up a map of the territory and figures out its location on it with increasing certainty. According to a recent study, London taxi drivers grow a larger posterior hippocampus, a brain region involved in memory and map making, as they learn the layout of the city. Perhaps they use similar probabilistic inference algorithms, with the notable difference that in the case of humans, drinking doesn’t seem to help.

Learning the Bayesian way

Now that we know how to (more or less) solve the inference problem, we’re ready to learn Bayesian networks from data, because for Bayesians learning is just another kind of probabilistic inference. All you have to do is apply Bayes’ theorem with the hypotheses as the possible causes and the data as the observed effect:

P(hypothesis | data) = P(hypothesis) ? P(data | hypothesis) / P(data)

The hypothesis can be as complex as a whole Bayesian network, or as simple as the probability that a coin will come up heads. In the latter case, the data is just the outcome of a series of coin flips. If, say, we obtain seventy heads in a hundred flips, a frequentist would estimate the probability of heads as 0.7. This is justified by the so-called maximum likelihood principle: of all the possible probabilities of heads, 0.7 is the one under which seeing seventy heads in a hundred flips is most likely. The likelihood of a hypothesis is P(data | hypothesis), and the principle says we should pick the hypothesis that maximizes it. Bayesians do something more subtle, though. They point out that we never know for sure which hypothesis is the true one, and so we shouldn’t just pick one hypothesis, like a value of 0.7 for the probability of heads; rather, we should compute the posterior probability of every possible hypothesis and entertain all of them when making predictions. The sum of the probabilities of all the hypotheses must be one, so if one becomes more likely, the others become less. For a Bayesian, in fact, there is no such thing as the truth; you have a prior distribution over hypotheses, after seeing the data it becomes the posterior distribution, as given by Bayes’ theorem, and that’s all.

This is a radical departure from the way science is usually done. It’s like saying, “Actually, neither Copernicus nor Ptolemy was right; let’s just predict the planets’ future trajectories assuming Earth goes round the sun and vice versa and average the results.”

Of course, it’s a weighted average, the weight of a hypothesis being its posterior probability, so a hypothesis that explains the data better will count for more. Still, as the joke goes, being Bayesian means never having to say you’re certain.

Needless to say, carrying around a multitude of hypotheses instead of just one is a huge pain. In the case of learning a Bayesian network, we’re supposed to make predictions by averaging over all possible Bayesian networks, including all possible graph structures and all possible parameter values for each structure. In some cases, we can compute the average over parameters in closed form, but with varying structures we’re out of luck. We have to resort to, for example, doing MCMC over the space of networks, jumping from one possible network to another as the Markov chain progresses. Combine all this complexity and computational cost with Bayesians’ controversial notion that there’s really no such thing as objective reality, and it’s not hard to see why frequentism has dominated science for the last century.

There’s a saving grace, however, and some major reasons to prefer the Bayesian way. The saving grace is that, most of the time, almost all hypotheses wind up with a tiny posterior probability, and we can safely ignore them. In fact, just considering the single most probable hypothesis is usually a very good approximation. Suppose our prior distribution for the coin flip problem is that all probabilities of heads are equally likely. The effect of seeing the outcomes of successive flips is to concentrate the distribution more and more on the hypotheses that best agree with the data. For example, if h ranges over the possible probabilities of heads and a coin comes out heads 70 percent of the time, we’ll see something like this:

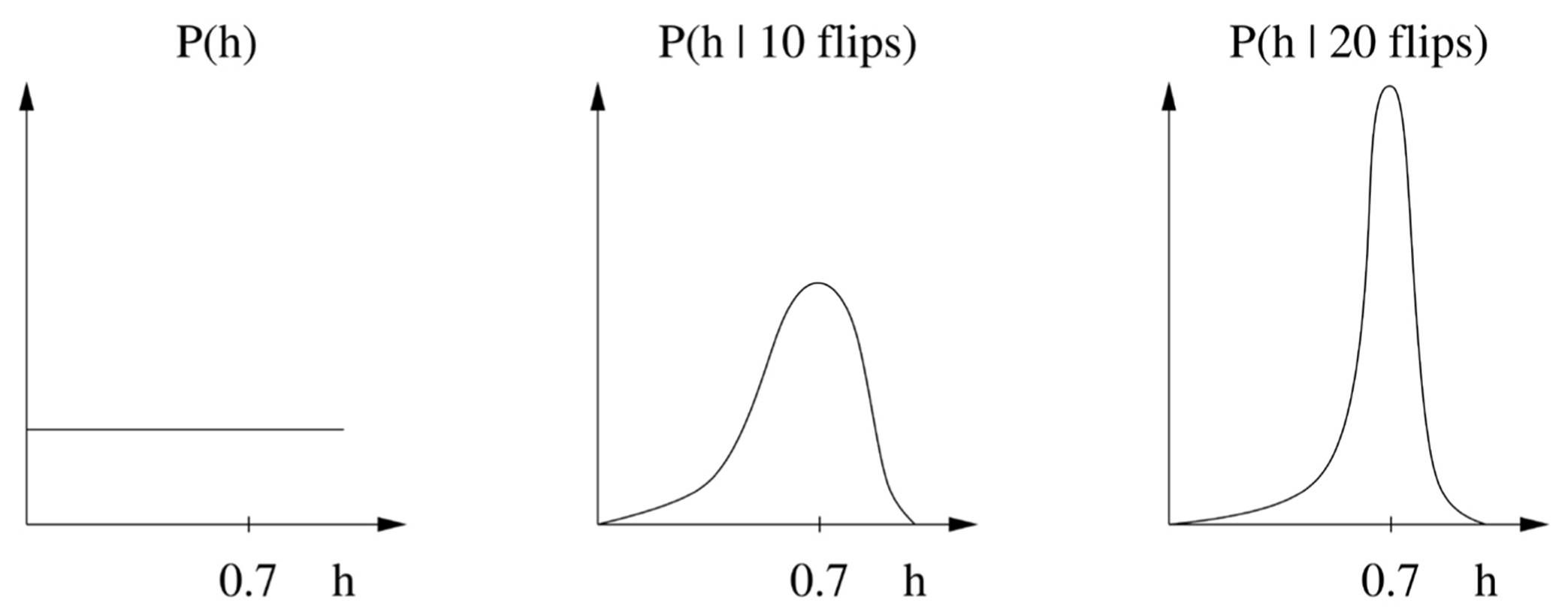
The posterior after each flip becomes the prior for the next flip, and flip by flip, we become increasingly certain that h = 0.7. If we just take the single most probable hypothesis (h = 0.7 in this case), the Bayesian approach becomes quite similar to the frequentist one, but with one crucial difference: Bayesians take the prior P(hypothesis) into account, not just the likelihood P(data | hypothesis). (The data prior P(data) can be ignored because it’s the same for all hypotheses and therefore doesn’t affect the choice of winner.) If we’re willing to assume that all hypotheses are equally likely a priori, the Bayesian approach now reduces to the maximum likelihood principle. So Bayesians can say to frequentists: “See, what you do is a special case of what we do, but at least we make our assumptions explicit.” And if the hypotheses are not equally likely a priori, maximum likelihood’s implicit assumption that they are leads to the wrong answers.

This might seem like a theoretical discussion, but it has tremendous practical consequences. If we’ve seen only one coin flip and it came out heads, maximum likelihood says that the probability of heads must be one. This could be wildly inaccurate and leaves us woefully unprepared for the coin coming up tails. Once we’ve seen a lot of flips, the estimate becomes more reliable, but in many problems, we never see enough flips, no matter how big the data. Suppose the word supercalifragilisticexpialidocious never appears in a spam e-mail in our training data and appears once in an e-mail talking about Mary Poppins. A Na?ve Bayes spam filter with maximum likelihood probability estimates will then decide that an e-mail containing it cannot be spam, regardless of whether every other word in the e-mail screams “Spam! Spam!” In contrast, a Bayesian would give the word a low but nonzero probability of appearing in spam, allowing the other words to override it.

The problem only gets worse if we try to learn the structure of a Bayesian network as well as its parameters. We can do this by hill climbing, starting with an empty network (no arrows), adding the arrow that most increases likelihood, and so on until no arrow causes an improvement. Unfortunately, this quickly leads to massive overfitting, with a network that assigns zero probability to all states not appearing in the data. Bayesians can do something much more interesting. They can use the prior distribution to encode experts’ knowledge about the problem-their answer to Hume’s question. For example, we can design an initial Bayesian network for medical diagnosis by interviewing doctors, asking them which symptoms they think depend on which diseases, and adding the corresponding arrows. This is the “prior network,” and the prior distribution can penalize alternative networks by the number of arrows that they add or remove from it. But doctors are fallible, so we’ll let the data override them: if the increase in likelihood from adding an arrow outweighs the penalty, we do it.

Of course, frequentists are aware of this issue, and their answer is to, for example, multiply the likelihood by a factor that penalizes more complex networks. But at this point frequentism and Bayesianism have become indistinguishable, and whether you call the scoring function “penalized likelihood” or “posterior probability” is really just a matter of taste.

Despite the convergence of frequentist and Bayesian thinking on some issues, there remains the philosophical difference about the meaning of probability. Viewing it as subjective makes many scientists queasy, but it also enables many otherwise-forbidden uses. If you’re a frequentist, you can only estimate probabilities of events that can occur more than once. So a question like “What is the probability that Hillary Clinton will beat Jeb Bush in the next presidential election?” is unanswerable, because there’s never been an election pitting them against each other. But for a Bayesian, a probability is a subjective degree of belief, so he’s free to make an educated guess, and the inference calculus keeps all his guesses consistent.

The Bayesian method is not just applicable to learning Bayesian networks and their special cases. (Conversely, despite their name, Bayesian networks aren’t necessarily Bayesian: frequentists can learn them, too, as we just saw.) We can put a prior distribution on any class of hypotheses-sets of rules, neural networks, programs-and then update it with the hypotheses’ likelihood given the data. Bayesians’ view is that it’s up to you what representation you choose, but then you have to learn it using Bayes’ theorem. In the 1990s, they mounted a spectacular takeover of the Conference on Neural Information Processing Systems (NIPS for short), the main venue for connectionist research. The ringleaders (so to speak) were David MacKay, Radford Neal, and Michael Jordan. MacKay, a Brit who was a student of John Hopfield’s at Caltech and later became chief scientific advisor to the UK’s Department of Energy, showed how to learn multilayer perceptrons the Bayesian way. Neal introduced the connectionists to MCMC, and Jordan introduced them to variational inference. Finally, they pointed out that in the limit you could “integrate out” the neurons in a multilayer perceptron, leaving a type of Bayesian model that made no reference to them. Before long, the word neural in the title of a paper submitted to NIPS became a good predictor of rejection. Some researchers joked that the conference should change its name to BIPS, for Bayesian Information Processing Systems.

Markov weighs the evidence

But something funny happened on the way to world domination. Researchers using Bayesian models kept noticing that you got better results by tweaking the probabilities in illegal ways. For example, raising P(words) to some power in speech recognizers improved accuracy, but then it wasn’t Bayes’ theorem any more. What was going on? The culprit, it turns out, was the false independence assumptions that generative models make. The simplified graph structure makes the models learnable and is worth keeping, but then we’re better off just learning the best parameters we can for the task at hand, irrespective of whether they’re probabilities. The real strength of, say, Na?ve Bayes is that it provides a small, informative set of features from which to predict the class and a fast, robust way to learn the corresponding parameters. In a spam filter, each feature is the occurrence of a particular word in spam, and the corresponding parameter is how often it occurs; and similarly for nonspam. Viewed in this way, Na?ve Bayes can be optimal, in the sense of making the best predictions possible, even in many cases where its independence assumptions are wildly violated. When I realized this and published a paper about it in 1996, people’s suspicion of Na?ve Bayes melted away, helping it to take off. But it was also a step on the way to a different kind of model, which in the last two decades has increasingly replaced Bayesian networks in machine learning: Markov networks.

A Markov network is a set of features and corresponding weights, which together define a probability distribution. A feature can be as simple as This is a ballad or as elaborate as This is a ballad by a hip-hop artist, with a saxophone riff and a descending chord progression. Pandora uses a large set of features, which it calls the Music Genome Project, to select songs to play for you. Suppose we plug them into a Markov network. If you like ballads, the weight of the corresponding feature goes up, and you’re more likely to hear ballads when you turn on Pandora. If you also like songs by hip-hop artists, that feature’s weight also goes up. The songs you’re most likely to hear are now ones that have both features, namely ballads by hip-hop artists. If you don’t like ballads or hip-hop artists per se, but only enjoy them in combination, the more elaborate feature Ballad by a hip-hop artist is what you need. Pandora’s features are handcrafted, but in Markov networks we can also learn features using hill climbing, similar to rule induction. Either way, gradient descent is a good way to learn the weights.

Like Bayesian networks, Markov networks can be represented by graphs, but they have undirected arcs instead of arrows. Two variables are connected, meaning they depend directly on each other, if they appear together in some feature, like Ballad and By a hip-hop artist in Ballad by a hip-hop artist.

Markov networks are a staple in many areas, such as computer vision. For instance, a driverless car needs to segment each image it sees into road, sky, and countryside. One option is to label each pixel as one of the three according to its color, but this is not nearly good enough. Images are very noisy and variable, and the car will hallucinate rocks strewn all over the roadway and patches of road in the sky. We know, however, that nearby pixels in an image are usually part of the same object, and we can introduce a corresponding set of features: for each pair of neighboring pixels, the feature is true if they belong to the same object, and false otherwise. Now images with large, contiguous blocks of road and sky are much more likely than images without, and the car goes straight instead of continually swerving left and right to avoid imaginary rocks.

Markov networks can be trained to maximize either the likelihood of the whole data or the conditional likelihood of what we want to predict given what we know. For Siri, the likelihood of the whole data is P(words, sounds), and the conditional likelihood we’re interested in is P(words | sounds). By optimizing the latter, we can ignore P(sounds), which is only a distraction from our goal. And since we ignore it, it can be arbitrarily complex. This is much better than HMMs’ unrealistic assumption that sounds depend solely on the corresponding words, without any influence from the surroundings. In fact, if all Siri cares about is figuring out which words you just spoke, perhaps it doesn’t even need to worry about probabilities; it just needs to make sure the correct words score higher than incorrect ones when it tots up the weights of their features-ideally a lot higher, just to be safe.

Analogizers took this line of reasoning to its logical conclusion, as we’ll see in the next chapter. In the first decade of the new millennium, they in turn took over NIPS. Now the connectionists dominate once more, under the banner of deep learning. Some say that research goes in cycles, but it’s more like a spiral, with loops winding around the direction of progress. In machine learning, the spiral converges to the Master Algorithm.

Logic and probability: The star-crossed couple

You’d think that Bayesians and symbolists would get along great, given that they both believe in a first-principles approach to learning, rather than a nature-inspired one. Far from it. Symbolists don’t like probabilities and tell jokes like “How many Bayesians does it take to change a lightbulb? They’re not sure. Come to think of it, they’re not sure the lightbulb is burned out.” More seriously, symbolists point to the high price we pay for probability. Inference suddenly becomes a lot more expensive, all those numbers are hard to understand, we have to deal with priors, and hordes of zombie hypotheses chase us around forever. The ability to compose pieces of knowledge on the fly, so dear to symbolists, is gone. Worst of all, we don’t know how to put probability distributions on many of the things we need to learn. A Bayesian network is a distribution over a vector of variables, but what about distributions over networks, databases, knowledge bases, languages, plans, and computer programs, to name a few? All of these are easily handled in logic, and an algorithm that can’t learn them is clearly not the Master Algorithm.

Bayesians, in turn, point to the brittleness of logic. If I have a rule like Birds fly, a world with even one flightless bird is impossible. If I try to patch things by adding exceptions, such as Birds fly, unless they’re penguins, I’ll never be done. (What about ostriches? Birds in cages? Dead birds? Birds with broken wings? Soaked wings?) A doctor diagnoses you with cancer, and you decide to get a second opinion. If the second doctor disagrees, you’re stuck. You can’t weigh the two opinions; you just have to believe them both. And then a catastrophe happens: pigs fly, perpetual motion is possible, and Earth doesn’t exist-because in logic everything can be inferred from a contradiction. Furthermore, if knowledge is learned from data, I can never be sure it’s true. Why do symbolists pretend otherwise? Surely Hume would frown on such insouciance.

Bayesians and symbolists agree that prior assumptions are inevitable, but they differ in the kinds of prior knowledge they allow. For Bayesians, knowledge goes in the prior distribution over the structure and parameters of the model. In principle, the parameter prior could be anything we please, but ironically, Bayesians tend to choose uninformative priors (like assigning the same probability to all hypotheses) because they’re easier to compute with. In any case, humans are not very good at estimating probabilities. For structure, Bayesian networks provide an intuitive way to incorporate knowledge: draw an arrow from A to B if you think that A directly causes B. But symbolists are much more flexible: you can provide as prior knowledge to your learner anything you can encode in logic, and practically anything can be encoded in logic-provided it’s black and white.

Clearly, we need both logic and probability. Curing cancer is a good example. A Bayesian network can model a single aspect of how cells function, like gene regulation or protein folding, but only logic can put all the pieces together into a coherent picture. On the other hand, logic can’t deal with incomplete or noisy information, which is pervasive in experimental biology, but Bayesian networks can handle it with aplomb.

Bayesian learning works on a single table of data, where each column represents a variable (for example, the expression level of one gene) and each row represents an instance (for example, a single microarray experiment, with each gene’s observed expression level). It’s OK if the table has “holes” and measurement errors because we can use probabilistic inference to fill in the holes and average over the errors. But if we have more than one table, Bayesian learning is stuck. It doesn’t know how to, for example, combine gene expression data with data about which DNA segments get translated into proteins, and how in turn the three-dimensional shapes of those proteins cause them to lock on to different parts of the DNA molecule, affecting the expression of other genes. In logic, we can easily write rules relating all of these aspects, and learn them from the relevant combinations of tables-but only provided the tables have no holes or errors.

Combining connectionism and evolutionism was fairly easy: just evolve the network structure and learn the parameters by backpropagation. But unifying logic and probability is a much harder problem. Attempts to do it go all the way back to Leibniz, who was a pioneer of both. Some of the best philosophers and mathematicians of the nineteenth and twentieth centuries, like George Boole and Rudolf Carnap, worked hard on it but ultimately didn’t get very far. More recently, computer scientists and AI researchers have joined the fray. But as the millennium turned around, the best we had were partial successes, like adding some logical constructs to Bayesian networks. Most experts believed that unifying logic and probability was impossible. The prospects for a Master Algorithm did not look good, particularly since the existing evolutionary and connectionist algorithms couldn’t deal with incomplete information or multiple data sets, either.

Luckily, we have since cracked the problem, and the Master Algorithm now looks that much closer. We’ll see how we did it in Chapter 9 and take it from there. But first we need to gather a very important, still-missing piece of the puzzle: how to learn from very little data. That might seem unnecessary in these days of data deluge, but the truth is that we often find ourselves with reams of data about some parts of the problem we want to solve and almost none about others. This is where one of the most important ideas in machine learning comes in: analogy. All of the tribes we’ve met so far have one thing in common: they learn an explicit model of the phenomenon under consideration, whether it’s a set of rules, a multilayer perceptron, a genetic program, or a Bayesian network. When they don’t have enough data to do that, they’re stumped. But analogizers can learn from as little as one example because they never form a model. Let’s see what they do instead.

Оглавление книги