Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER NINE: The Pieces of the Puzzle Fall into Place

CHAPTER NINE: The Pieces of the Puzzle Fall into Place

Machine learning is both a science and a technology, and both characteristics give us hints on how to unify it. On the science side, unifying theories often begin with a deceptively simple observation. Two seemingly unrelated phenomena turn out to be just two faces of the same coin, and like the first domino to fall, that realization sets off a cascade of others. An apple falling to the ground, the moon hanging in the sky: both are caused by gravity, and-apocryphal story or not-once Newton figured out how, gravity turned out to also account for the tides, the precession of the equinoxes, the trajectories of comets, and much else. In everyday experience, electricity and magnetism are never seen together: a lightning spark here, a rock that attracts iron objects there, both quite rare. But once Maxwell figured out how a changing electric field gives rise to magnetism and vice versa, it became clear that light itself is an intimate marriage of the two, and today we know that, far from rare, electromagnetism pervades all matter. Mendeleev’s periodic table not only organized all the known elements into just two dimensions, it also predicted where new elements would be found. Darwin’s observations aboard the Beagle suddenly began to make sense when Malthus’s Essay on Population suggested natural selection as the organizing principle. When Crick and Watson hit on the double helix structure as an explanation for the puzzling properties of DNA, they immediately saw how it might replicate itself, and biology’s transition from stamp collecting (in Rutherford’s pejorative words) to unified science had begun. In each of these cases, a bewildering variety of observations turned out to have a common cause, and once scientists identified it, they could in turn use it to predict many new phenomena. Similarly, even though the learners we’ve met in this book seem quite disparate-some based on the brain, some on evolution, some on abstract mathematical principles-they in fact have much in common, and the resulting theory of learning yields many new insights.

Although it is less well known, many of the most important technologies in the world are the result of inventing a unifier, a single mechanism that does what previously required many. The Internet, as the name implies, is a network that interconnects networks. Without it, every type of network would need a different protocol to talk to every other, much like we need a different dictionary for every pair of languages in the world. The Internet’s protocols are an Esperanto that gives each computer the illusion of talking directly to any other and that allows e-mail and the web to ignore the details of the physical infrastructure they flow over. Relational databases do something similar for enterprise applications, allowing developers and users to think in terms of the abstract relational model and ignore the different ways computers go about answering queries. A microprocessor is an assembly of digital electronic components that can mimic any other assembly. Virtual machines allow the same computer to pose as a hundred different computers to a hundred different people at the same time, and help make the cloud possible. Graphical user interfaces let us edit documents, spreadsheets, slide decks, and much else using a common language of windows, menus, and mouse clicks. The computer itself is a unifier: a single device capable of solving any logical or mathematical problem, provided we know how to program it. Even plain old electricity is a kind of unifier: you can generate it from many different sources-coal, gas, nuclear, hydro, wind, solar-and consume it in an infinite variety of ways. A power station doesn’t know or care how the electricity it produces will be consumed, and your porch light, dishwasher, or brand-new Tesla are oblivious to where their electricity supply comes from. Electricity is the Esperanto of energy. The Master Algorithm is the unifier of machine learning: it lets any application use any learner, by abstracting the learners into a common form that is all the applications need to know.

Our first step toward the Master Algorithm will be surprisingly simple. As it turns out, it’s not hard to combine many different learners into one, using what is known as metalearning. Netflix, Watson, Kinect, and countless others use it, and it’s one of the most powerful arrows in the machine learner’s quiver. It’s also a stepping-stone to the deeper unification that will follow.

Out of many models, one

Here’s a challenge: you have fifteen minutes to combine decision trees, multilayer perceptrons, classifier systems, Na?ve Bayes, and SVMs into a single algorithm possessing the best properties of each. Quick-what can you do? Clearly, it can’t involve the details of the individual algorithms; there’s no time for that. But how about the following? Think of each learner as an expert on a committee. Each looks carefully at the instance to be classified-what is the diagnosis for this patient?-and confidently makes its prediction. You’re not an expert yourself, but you’re the chair of the committee, and your job is to combine their recommendations into a final decision. What you have on your hands is in fact a new classification problem, where instead of the patient’s symptoms, the input is the experts’ opinions. But you can apply machine learning to this problem in the same way the experts applied it to the original one. We call this metalearning because it’s learning about the learners. The metalearner can itself be any learner, from a decision tree to a simple weighted vote. To learn the weights, or the decision tree, we replace the attributes of each original example by the learners’ predictions. Learners that often predict the correct class will get high weights, and inaccurate ones will tend to be ignored. With a decision tree, the choice of whether to use a learner can be contingent on other learners’ predictions. Either way, to obtain a learner’s prediction for a given training example, we must first apply it to the original training set excluding that example and use the resulting classifier-otherwise the committee risks being dominated by learners that overfit, since they can predict the correct class just by remembering it. The Netflix Prize winner used metalearning to combine hundreds of different learners. Watson uses it to choose its final answer from the available candidates. Nate Silver combines polls in a similar way to predict election results.

This type of metalearning is called stacking and is the brainchild of David Wolpert, whom we met in Chapter 3 as the author of the “no free lunch” theorem. An even simpler metalearner is bagging, invented by the statistician Leo Breiman. Bagging generates random variations of the training set by resampling, applies the same learner to each one, and combines the results by voting. The reason to do this is that it reduces variance: the combined model is much less sensitive to the vagaries of the data than any single one, making this a remarkably easy way to improve accuracy. If the models are decision trees and we further vary them by withholding a random subset of the attributes from consideration at each node, the result is a so-called random forest. Random forests are some of the most accurate classifiers around. Microsoft’s Kinect uses them to figure out what you’re doing, and they regularly win machine-learning competitions.

One of the cleverest metalearners is boosting, created by two learning theorists, Yoav Freund and Rob Schapire. Instead of combining different learners, boosting repeatedly applies the same classifier to the data, using each new model to correct the previous ones’ mistakes. It does this by assigning weights to the training examples; the weight of each misclassified example is increased after each round of learning, causing later rounds to focus more on it. The name boosting comes from the notion that this process can boost a classifier that’s only slightly better than random guessing, but consistently so, into one that’s almost perfect.

Metalearning is remarkably successful, but it’s not a very deep way to combine models. It’s also expensive, requiring as it does many runs of learning, and the combined models can be quite opaque. (“I believe you have prostate cancer because the decision tree, the genetic algorithm, and Na?ve Bayes say so, although the multilayer perceptron and the SVM disagree.”) Moreover, all the combined models are really just one big, messy model. Can’t we have a single learner that does the same job? Yes we can.

The Master Algorithm

Our unified learner is perhaps best introduced through an extended allegory. If machine learning is a continent divided into the territories of the five tribes, the Master Algorithm is its capital city, standing on the unique spot where the five territories meet. As you approach it from a distance, you can see that the city is made up of three concentric circles, each bounded by a wall. The outer and by far widest circle is Optimization Town. Each house here is an algorithm, and they come in all shapes and sizes. Some are under construction, the locals busy around them; some are gleaming new; and some look old and abandoned. Higher up the hill lies the Citadel of Evaluation. From its mansions and palaces orders issue continuously to the algorithms below. Above all, silhouetted against the sky, rise the Towers of Representation. Here live the rulers of the city. Their immutable laws set forth what can and cannot be done not just in the city but throughout the continent. Atop the central, tallest tower flies the flag of the Master Algorithm, red and black, with a five-pointed star surrounding an inscription that you cannot yet make out.

The city is divided into five sectors, each belonging to one of the five tribes. Each sector stretches down from its Tower of Representation to the city’s outer walls, encompassing the tower, a clutch of palaces in the Citadel of Evaluation, and the streets and houses in Optimization Town they overlook. The five sectors and three rings divide the city into fifteen districts, fifteen shapes, fifteen pieces of the puzzle you need to solve:

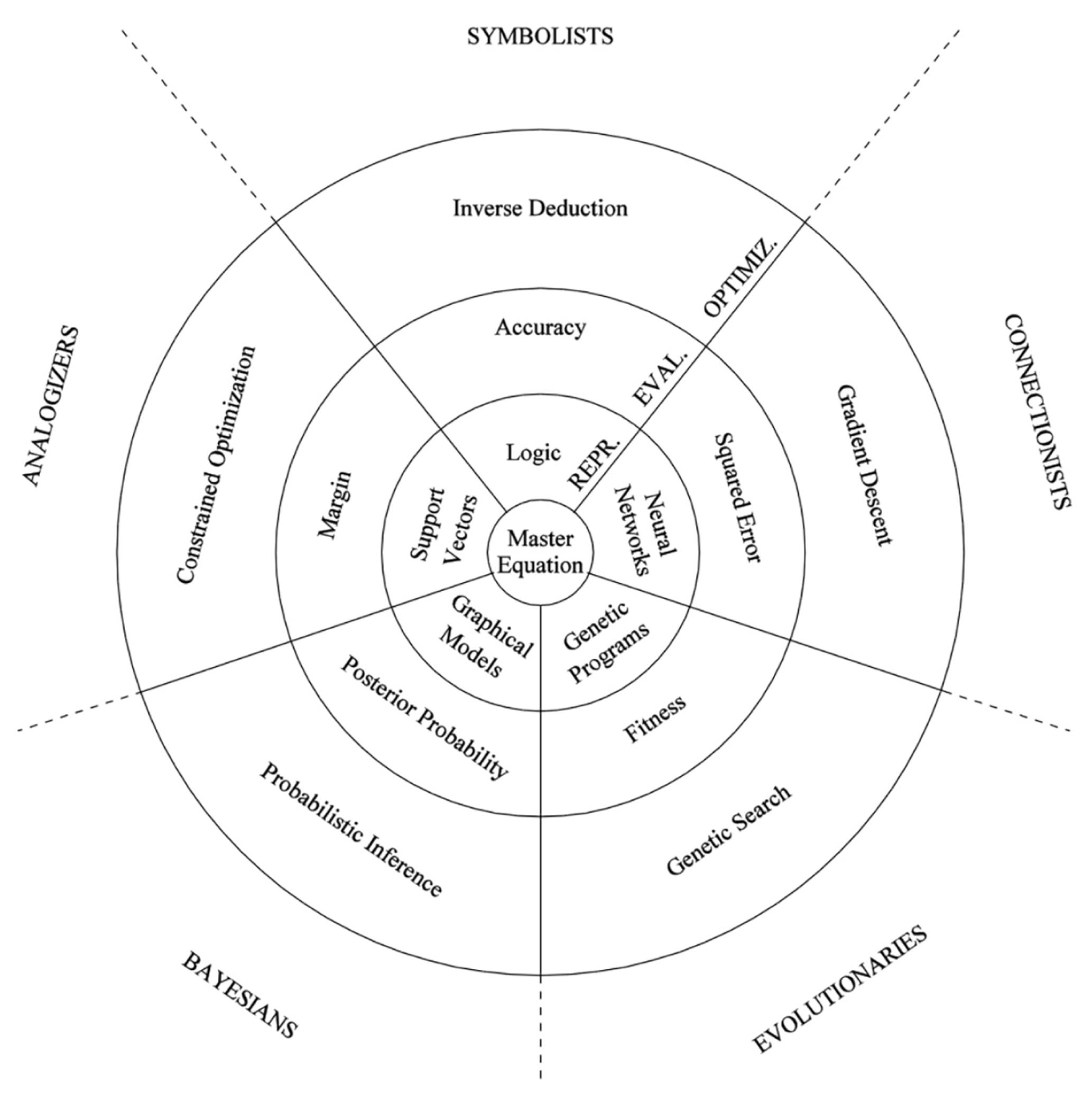
You gaze intently at the map, trying to decipher its secret. The fifteen pieces all match quite precisely, but you need to figure out how they combine to form just three: the representation, evaluation, and optimization components of the Master Algorithm. Every learner has these three elements, but they vary from tribe to tribe.

Representation is the formal language in which the learner expresses its models. The symbolists’ formal language is logic, of which rules and decision trees are special cases. The connectionists’ is neural networks. The evolutionaries’ is genetic programs, including classifier systems. The Bayesians’ is graphical models, an umbrella term for Bayesian networks and Markov networks. The analogizers’ is specific instances, possibly with weights, as in an SVM.

The evaluation component is a scoring function that says how good a model is. Symbolists use accuracy or information gain. Connectionists use a continuous error measure, such as squared error, which is the sum of the squares of the differences between the predicted values and the true ones. Bayesians use the posterior probability. Analogizers (at least of the SVM stripe) use the margin. In addition to how well the model fits the data, all tribes take into account other desirable properties, such as the model’s simplicity.

Optimization is the algorithm that searches for the highest-scoring model and returns it. The symbolists’ characteristic search algorithm is inverse deduction. The connectionists’ is gradient descent. The evolutionaries’ is genetic search, including crossover and mutation. The Bayesians are unusual in this regard: they don’t just look for the best model, but average over all models, weighted by how probable they are. To do the weighting efficiently, they use probabilistic inference algorithms like MCMC. The analogizers (or more precisely, the SVM mavens) use constrained optimization to find the best model.

After a long day’s journey, the sun is rapidly nearing the horizon, and you need to hurry before it gets dark. The city’s outer wall has five massive gates, each controlled by one of the tribes and leading to its district in Optimization Town. Let us enter through the Gradient Descent Gate, after whispering the watchword-“deep learning”-to the guard, and spiral in toward the Towers of Representation. From the gate the street ascends steeply up the hill to the citadel’s Squared Error Gate, but instead you turn left toward the evolutionary sector. The houses in the gradient descent district are all smooth curves and densely intertwined patterns, almost more like a jungle than a city. But when gradient descent gives way to genetic search, the picture changes abruptly. Here the houses rise higher, with structure piled on structure, but the structures are spare, almost vacant, as if waiting to be filled in by gradient descent’s curves. That’s it: the way to combine the two is to use genetic search to find the structure of the model and let gradient descent fill in its parameters. This is what nature does: evolution creates brain structures, and individual experience modulates them.

The first step accomplished, you hurry on to the Bayesian district. Even from a distance, you can see how it clusters around the Cathedral of Bayes’ Theorem. MCMC Alley zigzags randomly along the way. This is going to take a while. You take a shortcut onto Belief Propagation Street, but it seems to loop around forever. Then you see it: the Most Likely Avenue, rising majestically toward the Posterior Probability Gate. Rather than average over all models, you can head straight for the most probable one, confident that the resulting predictions will be almost the same. And you can let genetic search pick the model’s structure and gradient descent its parameters. With a sigh of relief, you realize that’s all the probabilistic inference you’ll need, at least until it’s time to answer questions using the model.

You keep going. The constrained optimization district is a maze of narrow alleys and dead ends, examples of all kinds standing cheek by jowl everywhere, with an occasional clearing around a support vector. Clearly, all you need to do to avoid bumping into examples of the wrong class is add constraints to the optimizer you’ve already assembled. But come to think of it, not even that is necessary. When we learn SVMs, we usually let margins be violated in order to avoid overfitting, provided each violation pays a penalty. In this case the optimal example weights can again be learned by a form of gradient descent. That was easy. You feel like you’re starting to get the hang of it.

The dense ranks of instances end abruptly, and you find yourself in the inverse deduction district, a place of broad avenues and ancient stone buildings. The architecture here is geometric, austere, made of straight lines and right angles. Even the severely pruned trees have rectangular trunks, and their leaves are meticulously labeled with class predictions. The denizens of this district seem to build their houses in a peculiar way: they start with the roof, which they label “Conclusions,” and gradually fill in the gaps between it and the ground, which they label “Premises.” One by one, they find a stone block that’s the right shape to fill in a particular gap and hoist it up to its place. But, you notice, many gaps have the same shape, and it would be faster to cut and combine blocks until they form that shape, and then repeat the process as many times as necessary. In other words, you could use genetic search to do inverse deduction. Neat. It looks like you’ve boiled down the five optimizers to a simple recipe: genetic search for structure and gradient descent for parameters. And even that may be overkill. For a lot of problems, you can whittle genetic search down to hill climbing if you do three things: leave out crossover, try all possible point mutations in each generation, and always select the single best hypothesis to seed the next generation.

What’s that statue up ahead? Aristotle, looking rather disapprovingly toward the tangled mess of the gradient descent quarter. You’ve come full circle. You have the unified optimizer you need for the Master Algorithm, but this is no time to congratulate yourself. Night has fallen, and you still have much to do. You enter the Citadel of Evaluation through the imposing but rather narrow Accuracy Gate. The inscription above it says “Abandon all hope of overfitting, ye who enter here.” As you circle past the palaces of the five tribes’ evaluators, you mentally snap the pieces into place. You use accuracy to evaluate yes-or-no predictions and squared error for continuous ones. Fitness is just the evolutionaries’ name for the scoring function; you can make it anything you want, including accuracy and squared error. Posterior probability reduces to squared error if you ignore the prior probability and the errors follow a normal distribution. The margin, if you allow it to be violated for a price, becomes a softer version of accuracy: instead of paying no penalty for a correct prediction and a penalty of one for an incorrect prediction, the penalty is zero until you get inside the margin, at which point it starts to steadily go up. Whew! Combining the evaluators was a lot easier than combining the optimizers. But the Towers of Representation, looming above you, fill you with a sense of foreboding.

You’ve reached the final stage of your quest. You knock on the door of the Tower of Support Vectors. A menacing-looking guard opens it, and you suddenly realize that you don’t know the password. “Kernel,” you blurt out, trying to keep the panic from your voice. The guard bows and steps aside. Regaining your composure, you step in, mentally kicking yourself for your carelessness. The entire ground floor of the tower is taken up by a lavishly appointed circular chamber, with what seems to be a marble representation of an SVM occupying pride of place at the center. As you walk around it, you notice a door on the far side. It must lead to the central tower-the Tower of the Master Algorithm. The door seems unguarded. You decide to take a shortcut. Slipping through the doorway, you walk down a short corridor and find yourself in an even larger pentagonal chamber, with a door in each wall. In the center, a spiral staircase rises as high as the eye can see. You hear voices above and duck into the doorway opposite. This one leads to the Tower of Neural Networks. Once again you’re in a circular chamber, this one with a sculpture of a multilayer perceptron as the centerpiece. Its parts are different from the SVM’s, but their arrangement is remarkably similar. Suddenly you see it: an SVM is just a multilayer perceptron with a hidden layer composed of kernels instead of S curves and an output that’s a linear combination instead of another S curve.

Could it be that the other representations also have a similar form? With rising excitement, you run back through the pentagonal chamber and into the Tower of Logic. Staring at the depiction of a set of rules in the center, you try to discern a pattern. Yes! Each rule is just a highly stylized neuron. For example, the rule If it’s a giant reptile and breathes fire then it’s a dragon is just a perceptron with weights of one for it’s a giant reptile and breathes fire and a threshold of 1.5. And a set of rules is a multilayer perceptron with a hidden layer containing one neuron for each rule and an output neuron to form the disjunction of the rules. There’s a nagging doubt in the back of your mind, but you don’t have time for it right now. As you cross the pentagonal chamber to the Tower of Genetic Programs, you can already see how to bring them into the fold. Genetic programs are just programs, and programs are just logic constructs. The sculpture of a genetic program in the chamber is in the shape of a tree, subroutines branching into more subroutines, and when you look closely at the leaves, you can see that they’re just simple rules. So programs boil down to rules, and if rules can be reduced to neurons, so can programs.

On to the Tower of Graphical Models. Unfortunately, the sculpture in its circular chamber looks nothing like the others. A graphical model is a product of factors: conditional probabilities, in the case of Bayesian networks, and non-negative functions of the state, in the case of Markov networks. Try as you might, you just can’t see the connection to neural networks or sets of rules. Disappointment washes over you. But then you put on your “loggles,” which replace every function by its logarithm. Eureka-the product of factors is now a sum of terms, just like an SVM, a voting set of rules, or a multilayer perceptron without the output S curve. For example, you can translate a Na?ve Bayes dragon classifier into a perceptron whose weight for breathes fire is the log of P(breathes fire | dragon) minus the log of P(breathes fire | not dragon). But of course, graphical models are much more general than this because they can represent probability distributions over many variables, not just the distribution of one variable (the class) given the others (the attributes).

You did it! Or did you? Absorbing SVMs into neural networks and neural networks into graphical models: that worked. So did absorbing genetic programs into logic. But combining logic and graphical models? Something is amiss there. Belatedly, you see the problem: logic has a dimension that graphical models lack and vice versa. The sculptures in the five chambers matched because they were simple allegories, but the reality doesn’t. Graphical models don’t let us represent rules involving more than one object, like Friends of friends are friends; all their variables have to be properties of the same object. They also can’t represent arbitrary programs, which pass sets of variables from one subroutine to another. Logic can easily do both of these things, but on the other hand it can’t represent uncertainty, ambiguity, or degrees of similarity. And without a representation that can do all of these things, you don’t have a universal learner.

You rack your brains for a solution, but the more you try, the harder it gets. Perhaps unifying logic and probability is just beyond human ability. Exhausted, you fall asleep. A deep growl jolts you awake. The hydra-headed complexity monster pounces on you, jaws snapping, but you duck at the last moment. Slashing desperately at the monster with the sword of learning, the only one that can slay it, you finally succeed in cutting off all its heads. Before it can grow new ones, you run up the stairs.

After an arduous climb, you reach the top. A wedding is in progress. Praedicatus, First Lord of Logic, ruler of the symbolic realm and Protector of the Programs, says to Markovia, Princess of Probability, Empress of Networks: “Let us unite our realms. To my rules thou shalt add weights, begetting a new representation that will spread far across the land.” The princess says, “And we shall call our progeny Markov logic networks.”

Your head is spinning. You go outside to the balcony. The sun has risen over the city. You gaze out over the rooftops to the countryside beyond. Forests of servers stretch away in all directions, humming quietly, waiting for the Master Algorithm. Convoys move along the roads, carrying gold from the data mines. Far to the west, the land gives way to a sea of information, dotted with ships. You look up at the flag of the Master Algorithm. You can now clearly see the inscription inside the five-pointed star:

P = e ^w•n / Z

What could this mean, you wonder?

Markov logic networks

In 2003, I started thinking about the problem of how to unify logic and probability, together with my student Matt Richardson. At first we made little progress because we were trying to do it with Bayesian networks, and their rigid form-a strict order on variables, conditional distributions of children given parents-is incompatible with the flexibility of logic. But the day before Christmas Eve, I realized there was a much better way. If we switched to Markov networks, we could use any logical formula as a template for Markov network features, and that would unify logic and graphical models. Let’s see how.

Recall that a Markov network is defined by a weighted sum of features, much like a perceptron. Suppose we have a collection of photos of people. We pick a random one and compute features of it like The person has gray hair, The person is old, The person is a woman, and so on. In a perceptron, we pass the weighted sum of these features through a threshold to decide whether, say, the person is your grandmother or not. In a Markov network, we do something very different (at least at first sight): we exponentiate the weighted sum, turning it into a product of factors, and this product is the probability of choosing that particular picture from the collection, regardless of whether your grandmother is in it. If you have many pictures of old people, the weight of that feature goes up. If most of them are of men, the weight of The person is a woman goes down. The features can be anything we want, making Markov networks a remarkably flexible way to represent probability distributions.

Actually, I lied: the product of factors is not yet a probability because the probabilities of all pictures must add up to one, and there’s no guarantee that the products of factors for all pictures will do so. We need to normalize them, meaning divide each product by the sum of all of them. The sum of all the normalized products is then guaranteed to be one because it’s just a number divided by itself. The probability of a picture is thus the weighted sum of its features, exponentiated and normalized. If you look back at the equation in the five-pointed star, you’ll probably start to get an inkling of what it means. P is a probability, w is a vector of weights (notice it’s in boldface), n is a vector of numbers, and their dot product • is exponentiated and divided by Z, the sum of all products. If we let the first component of n be one if the first feature of the image is true and zero otherwise, and so on, w•n is just a shorthand for the weighted sum of features we’ve been talking about all along.

So the equation gives the probability of an image (or whatever) according to a Markov network. But it’s more general than that because it’s not just the equation of a Markov network; rather, it’s the equation of a Markov logic network, as we call it. In a Markov logic network, or MLN for short, the numbers in n don’t have to be just zero or one, and they don’t refer to features-they refer to logical formulas. At the end of Chapter 8, we saw how we can go beyond Markov networks to relational models, which are defined in terms of feature templates, not just features. Alice and Bob both have the flu is a feature specific to Alice and Bob. X and Y both have the flu is a feature template, which can be instantiated with Alice and Bob, Alice and Chris, and any other two people. A feature template is a powerful thing because it can summarize billions of features or more in a single short expression. But we need a formal language to define feature templates, and we have one readily available: logic.

An MLN is just a set of logical formulas and their weights. When applied to a particular set of entities, it defines a Markov network over their possible states. For example, if the entities are Alice and Bob, a possible state is that Alice and Bob are friends, Alice has the flu, and so does Bob. Let’s suppose the MLN has two formulas: Everyone has the flu and If someone has the flu, so do their friends. In standard logic, this would be a pretty useless pair of statements: the first would rule out any state with even a single healthy person, and the second would be redundant. But in an MLN, the first formula just means that there’s a feature X has the flu for every person X, with the same weight as the formula. If people are likely to have the flu, the formula will have a high weight, and so will the corresponding features. A state with many healthy people is less probable than one with few, but not impossible. And because of the second formula, a state where someone has the flu and their friends don’t is less probable than one where healthy and infected people fall into separate clusters of friends.

At this point you can probably guess what the n in the master equation is: its first component is the number of true instances of the first formula in the state, the second is the number of true instances of the second formula, and so on. If we’re looking at a group of ten friends and seven of them have the flu, the first component of n is seven, and so on. (Shouldn’t the probability be different if seven out of twenty instead of seven out of ten friends have the flu? Yes, and it is, because of Z.) In the limit, if we let all the weights go to infinity, Markov logic reduces to standard logic because violating a single instance of a formula then causes the probability to collapse to zero, making the state impossible. On the probabilistic side, an MLN reduces to a Markov network when all the formulas talk about a single object. So Markov logic includes both logic and Markov networks as special cases, and it’s the unification we were looking for.

Learning an MLN means discovering formulas that are true in the world more often than random chance would predict, and figuring out the weights for those formulas that cause their predicted probabilities to match their observed frequencies. Once we’ve learned an MLN, we can use it to answer questions like “What is the probability that Bob has the flu, given that he’s friends with Alice and she has the flu?” And guess what? It turns out that the probability is given by an S curve applied to the weighted sum of features, much as in a multilayer perceptron. And an MLN with long chains of rules can represent a deep neural network, with one layer per link in the chain.

Of course, don’t be deceived by the simple MLN above for predicting the spread of flu. Picture instead an MLN for diagnosing and curing cancer. The MLN represents a probability distribution over the states of a cell. Every part of the cell, every organelle, every metabolic pathway, every gene and protein is an entity in the MLN, and the MLN’s formulas encode the dependencies between them. We can ask the MLN, “Is this cell cancerous?” and probe it with different drugs and see what happens. We don’t have an MLN like this yet, but later in this chapter I’ll envisage how it might come about.

To recap: the unified learner we’ve arrived at uses MLNs as the representation, posterior probability as the evaluation function, and genetic search coupled with gradient descent as the optimizer. If we want, we can easily replace the posterior by some other accuracy measure, or genetic search by hill climbing. We’ve ascended a high peak, and now we can enjoy the view. I wouldn’t be so rash as to call this learner the Master Algorithm, however. For one, the proof of the pudding is in the eating, and although over the last decade this algorithm (or variations of it) has been successfully applied in many areas, there are many more to which it hasn’t, and so it’s not yet clear just how general purpose it is. Second, there are some important problems that it doesn’t solve. But before we look at them, let’s look at what it can do.

From Hume to your housebot

You can download the learner I’ve just described from alchemy.cs.washington.edu. We christened it Alchemy to remind ourselves that, despite all its successes, machine learning is still in the alchemy stage of science. If you do download it, you’ll see that it includes a lot more than the basic algorithm I’ve described but also that it is still missing a few things I said the universal learner ought to have, like crossover. Nevertheless, let’s use the name Alchemy to refer to our candidate universal learner for simplicity.

Alchemy addresses Hume’s original question by having another input besides the data: your initial knowledge, in the form of a set of logical formulas, with or without weights. The formulas can be inconsistent, incomplete, or even just plain wrong; the learning and probabilistic reasoning will take care of that. The key point is that Alchemy doesn’t have to learn from scratch. In fact, we can even tell Alchemy to keep the formulas unchanged and learn only the weights. In this case, giving Alchemy the appropriate formulas can turn it into a Boltzmann machine, a Bayesian network, an instance-based learner, and many other models. This explains why we can have a universal learner despite the “no free lunch” theorem. Rather, Alchemy is like an inductive Turing machine, which we can program to behave as a very powerful or a very restricted learner; it’s up to us. Alchemy provides a unifier for machine learning in the same way that the Internet provides one for computer networks, the relational model for databases, or the graphical user interface for everyday applications.

Of course, even if you use Alchemy with no initial formulas (and you can), that doesn’t make it knowledge-free. The choice of formal language, score function, and optimizer implicitly encodes assumptions about the world. So it’s natural to ask whether we can have an even more general learner than Alchemy. What did evolution assume when it began its long journey from the first bacteria to all the life-forms around today? I think there’s a simple assumption from which all else follows: the learner is part of the world. This means that the learner as a physical system obeys the same laws as its environment, whatever they are, and therefore already “knows” them implicitly and is primed to discover them. In the next section, we’ll see what this can mean concretely and how to embody it in Alchemy. But for the moment, let’s note that it’s perhaps the best answer we can ever give to Hume’s question. On the one hand, assuming the learner is part of the world is an assumption-in principle, the learner could obey different laws from those the world obeys-so it satisfies Hume’s dictum that learning is only possible with prior knowledge. On the other hand, it’s an assumption so basic and hard to disagree with that perhaps it’s all we need for this world.

At the other extreme, knowledge engineers-the most determined critics of machine learning-have good reason to like Alchemy. Instead of a basic model structure or a few rough guesses, Alchemy can input a large, lovingly assembled knowledge base, if it’s available. Because probabilistic rules can interact in much richer ways than deterministic ones, manually encoded knowledge goes a longer way in Markov logic. And since knowledge bases in Markov logic don’t have to be self-consistent, they can be very large and accommodate many different contributors without falling apart-a goal that has so far eluded knowledge engineers.

Most of all, though, Alchemy addresses the problems that each of the five tribes of machine learning has worked on for so long. Let’s look at each of them in turn.

Symbolists combine different pieces of knowledge on the fly, in the same way that mathematicians combine axioms to prove theorems. This contrasts sharply with neural networks and other models with a fixed structure. Alchemy does it using logic, as symbolists do, but with a twist. To prove a theorem in logic, you need to find only one sequence of axiom applications that produces it. Because Alchemy reasons probabilistically, it does more: it finds multiple sequences of formulas that lead to the theorem or its negation and weighs them to compute the theorem’s probability of being true. This way it can reason not just about mathematical universals, but about whether “the president” in a news story means “Barack Obama,” or what folder an e-mail should be filed in. The symbolists’ master algorithm, inverse deduction, postulates new logical rules needed to serve as steps between the data and a desired conclusion. Alchemy introduces new rules by hill climbing, starting with the initial rules and constructing rules that, combined with the initial ones and the data, make the conclusions more likely.

Connectionists’ models are inspired by the brain, with networks of S curves that correspond to neurons and weighted connections between them corresponding to synapses. In Alchemy, two variables are connected if they appear together in some formula, and the probability of a variable given its neighbors is an S curve. (Although I won’t show why, it’s a direct consequence of the master equation we saw in the previous section.) The connectionists’ master algorithm is backpropagation, which they use to figure out which neurons are responsible for which errors and adjust their weights accordingly. Backpropagation is a form of gradient descent, which Alchemy uses to optimize the weights of a Markov logic network.

Evolutionaries use genetic algorithms to simulate natural selection. A genetic algorithm maintains a population of hypotheses and in each generation crosses over and mutates the fittest ones to produce the next generation. Alchemy maintains a population of hypotheses in the form of weighted formulas, modifies them in various ways at each step, and keeps the variations that most increase the posterior probability of the data (or some other score function). If the population is a single hypothesis, this reduces to hill climbing. The current open-source implementation of Alchemy does not include crossover, but this would be a straightforward addition. The evolutionaries’ master algorithm is genetic programming, which applies crossover and mutation to computer programs represented as trees of subroutines. Trees of subroutines can be represented by sets of logical rules, and the Prolog programming language does just that. In Prolog, each rule corresponds to a subroutine, and its antecedents are the subroutines it calls. So we can think of Alchemy with crossover as genetic programming using a Prolog-like programming language, with the added advantage that the rules can be probabilistic.

Bayesians believe that modeling uncertainty is the key to learning and use formal representations like Bayesian networks and Markov networks to do so. As we already saw, Markov networks are a special type of MLN. Bayesian networks are also easily represented using the MLN master equation, with a feature for each possible state of a variable and its parents, and the logarithm of the corresponding conditional probability as its weight. (The normalization constant Z then conveniently reduces to 1, meaning we can ignore it.) Bayesians’ master algorithm is Bayes’ theorem, implemented using probabilistic inference algorithms like belief propagation and MCMC. As you may have noticed, Bayes’ theorem is a special case of the master equation, with P = P(A|B), Z = P(B), and features and weights corresponding to P(A) and P(B|A). The Alchemy system includes both belief propagation and MCMC for inference, generalized to handle weighted logical formulas. Using probabilistic inference over the proof paths provided by logic, Alchemy weighs the evidence for and against a conclusion and outputs the probability of the conclusion. This contrasts with the “plain vanilla” logic used by symbolists, which is all or none and so falls apart when given contradictory evidence.

Analogizers learn by hypothesizing that entities with similar known properties have similar unknown ones: patients with similar symptoms have similar diagnoses, readers who bought the same books in the past will do so again in the future, and so on. MLNs can represent similarity between entities with formulas like People with the same tastes buy the same books. Then the more of the same books Alice and Bob have bought, the more likely they are to have the same tastes, and (applying the same formula in the opposite direction) the more likely Alice is to buy a book if Bob also did. Their similarity is represented by their probability of having the same tastes. To make this really useful, we can have different weights for different instances of the same rule: if Alice and Bob both bought a certain rare book, this is probably more informative than if they both bought a best seller and should therefore have a higher weight. In this case the properties whose similarity we’re computing are discrete (bought/not bought), but we can also represent similarity between continuous properties, like the distance between two cities, by letting an MLN have these similarities as features. If the evaluation function is a margin-style score function instead of the posterior probability, the result is a generalization of SVMs, the analogizers’ master algorithm. A greater challenge for our master learner is reproducing structure mapping, the more powerful type of analogy that can make inferences from one domain (e.g., the solar system) to another (the atom). We can do this by learning formulas that don’t refer to any of the specific relations in the source domain. For example, Friends of smokers also smoke is about friendship and smoking, but Related entities have similar properties applies to any relation and property. We can learn it by generalizing from Friends of friends also smoke, Coworkers of experts are also experts, and other such patterns in a social network and then apply it to, say, the web, with instances like Interesting pages link to interesting pages, or to molecular biology, with instances like Proteins that interact with gene-regulating proteins also regulate genes. Researchers in my group and others have done all of these things, and more.

Alchemy also enables the five types of unsupervised learning we saw in the previous chapter. It does relational learning, obviously, and in fact that’s where most of its applications to date have been. Alchemy uses logic to represent relations among entities and Markov networks to let them be uncertain. We can turn Alchemy into a reinforcement learner by wrapping delayed rewards around it and using it to learn the value of each state in the same way that traditional reinforcement learners use, say, a neural network. We can do chunking in Alchemy by adding a new operation that condenses chains of rules into single rules. (For example, If A then B and If B then C into If A then C.) An MLN with a single unobserved variable connected to all the observable ones does clustering. (An unobserved variable is a variable whose values we never see in the data; it’s “hidden,” so to speak, and can only be inferred.) MLNs with more than one unobserved variable do a kind of discrete dimensionality reduction by inferring the values of those (fewer) variables from the (more numerous) observable ones. Alchemy can also handle MLNs with continuous unobserved variables, which would be needed to do things like principal-component analysis and Isomap. So Alchemy can in principle do all the things we want Robby the robot to do, or at least all the things we’ve discussed in this book. Indeed, we’ve used Alchemy to let a robot learn a map of its environment, figuring out from its sensors where the walls and doors are, their angles and distances, and so on, which is the first step in building a competent housebot.

Finally, we can turn Alchemy into a metalearner like stacking by encoding the individual classifiers as MLNs and adding or learning formulas to combine them. This is what DARPA did in its PAL project. PAL, the Personalized Assistant that Learns, was the largest AI project in DARPA history and the progenitor of Siri. PAL’s goal was to build an automated secretary. It used Markov logic as its overarching representation, combining the outputs from different modules into the final decisions on what to do. This also allowed PAL’s modules to learn from each other by evolving toward a consensus.

One of Alchemy’s largest applications to date was to learn a semantic network (or knowledge graph, as Google calls it) from the web. A semantic network is a set of concepts (like planets and stars) and relations among those concepts (planets orbit stars). Alchemy learned over a million such patterns from facts extracted from the web (e.g., Earth orbits the sun). It discovered concepts like planet all by itself. The version we used was more advanced than the basic one I’ve described here, but the essential ideas are the same. Various research groups have used Alchemy or their own MLN implementations to solve problems in natural language processing, computer vision, activity recognition, social network analysis, molecular biology, and many other areas.

Despite its successes, Alchemy has some significant shortcomings. It does not yet scale to truly big data, and someone without a PhD in machine learning will find it hard to use. Because of these problems, it’s not yet ready for prime time. But let’s see what we can do about them.

Planetary-scale machine learning

In computer science, a problem isn’t really solved until it’s solved efficiently. Knowing how to do something isn’t much use if you can’t do it within the available time and memory, and these can run out very quickly when you’re dealing with an MLN. We routinely learn MLNs with millions of variables and billions of features, but this is not as large as it seems because the number of variables grows very quickly with the number of entities in the MLN: if you have a social network with a thousand people, you already have a million possible pairs of friends and a billion instances of the formula Friends of friends are friends.

Inference in Alchemy is a combination of logical and probabilistic inference. The former is done by proving theorems and the latter by belief propagation, MCMC, and the other methods we saw in Chapter 6. We’ve combined the two into probabilistic theorem proving, and the unified inference algorithm, capable of computing the probability of any logical formula, is a key part of the current Alchemy system. But it can be very computationally expensive. If your brain used probabilistic theorem proving, the proverbial tiger would eat you before you figured out to run away. That’s a high price to pay for the generality of Markov logic. Your brain, having evolved in the real world, must encode additional assumptions that allow it to do inference very efficiently. In the last few years, we’ve started to figure out what they might be and encode them into Alchemy.

The world is not a random jumble of interactions; it has a hierarchical structure: galaxies, planets, continents, countries, cities, neighborhoods, your house, you, your head, your nose, a cell on its tip, the organelles in it, molecules, atoms, subatomic particles. The way to model it, then, is with an MLN that also has a hierarchical structure. This is an example of the assumption that the learner and its environment are alike. The MLN doesn’t have to know a priori which parts the world is composed of; all Alchemy has to do is assume that the world has parts and look for them, rather like a newly made bookshelf assumes that there are books but doesn’t yet know which ones will be placed on it. Hierarchical structure helps make inference tractable because subparts of the world interact mostly with other subparts of the same part: neighbors talk more to each other than to people in another country, molecules produced in one cell react mostly with other molecules in that cell, and so on.

Another property of the world that makes learning and inference easier is that the entities in it don’t come in arbitrary forms. Rather, they fall into classes and subclasses, with members of the same class being more alike than members of different ones. Alive or inanimate, animal or plant, bird or mammal, human or not: if we know all the distinctions relevant to the question at hand, we can lump together all the entities that lack them and that can save a lot of time. As before, the MLN doesn’t have to know a priori what the classes in the world are; it can learn them from data by hierarchical clustering.

The world has parts, and parts belong to classes: combining these two gives us most of what we need to make inference in Alchemy tractable. We can learn the world’s MLN by breaking it into parts and subparts, such that most interactions are between subparts of the same part, and then grouping the parts into classes and subclasses. If the world is a Lego toy, we can break it up into individual bricks, remembering which attaches to which, and group the bricks by shape and color. If the world is Wikipedia, we can extract the entities it talks about, group them into classes, and learn how classes relate to each other. Then if someone asks us “Is Arnold Schwarzenegger an action star?” we can answer yes, because he’s a star and he’s in action movies. Step-by-step, we can learn larger and larger MLNs, until we’re doing what a friend of mine at Google calls “planetary-scale machine learning”: modeling everyone in the world at once, with data continually streaming in and answers streaming out.

Of course, learning on this scale requires much more than a direct implementation of the algorithms we’ve seen. For one, beyond a certain point a single processor is not enough; we have to distribute the learning over many servers. Researchers in both industry and academia have intensely investigated how to, for example, do gradient descent using many computers in parallel. One option is to divide the data among the processors; another is to divide the model’s parameters. After each step, we combine the results and redistribute the work. Either way, doing this without letting the cost of communication overwhelm you, or the quality of the results suffer, is far from trivial. Another issue is that, if you have an endless stream of data coming in, you can’t wait to see it all before you commit to some decisions. One solution is to use the sampling principle: if you want to predict who will win the next presidential election, you don’t need to ask every voter who he or she will vote for; a sample of a few thousand suffices, if you’re willing to accept a little bit of uncertainty. The trick is to generalize this to complex models with millions of parameters. But we can do this by taking at each step just as many examples from the stream as we need to be pretty sure that we’re making the right decision and that the total uncertainty over all the decisions stays within bounds. That way we can effectively learn from infinite data in finite time, as I put it in an early paper proposing this approach.

Big-data systems are the Cecil B. DeMille productions of machine learning, with thousands of servers instead of thousands of extras. In the largest projects, just getting all the data together, verifying it, cleaning it up, and munging it into a form the learners can digest can make building the pyramids seem like a walk in the park. At the pharaonic end, Europe’s FuturICT project aims to build a model of-literally-the whole world. Societies, governments, culture, technology, agriculture, disease, the global economy: nothing is to be left out. This is surely premature, but it does foreshadow the shape of things to come. In the meantime, projects like this can help us find out where the limits of scalability are and how to overcome them.

Computational complexity is one thing, but human complexity is another. If computers are like idiot savants, learning algorithms can sometimes come across like child prodigies prone to temper tantrums. That’s one reason humans who can wrangle them into submission are so highly paid. If you know how to expertly tweak the control knobs until they’re just right, magic can ensue, in the form of a stream of insights beyond the learner’s years. And, not unlike the Delphic oracle, interpreting the learner’s pronouncements can itself require considerable skill. Turn the knobs wrong, though, and the learner may spew out a torrent of gibberish or clam up in defiance. Unfortunately, in this regard Alchemy is no better than most. Writing down what you know in logic, feeding in the data, and pushing the button is the fun part. When Alchemy returns a beautifully accurate and efficient MLN, you go down to the pub and celebrate. When it doesn’t-which is most of the time-the battle begins. Is the problem in the knowledge, the learning, or the inference? On the one hand, because of the learning and probabilistic inference, a simple MLN can do the job of a complex program. On the other, when it doesn’t work, it’s much harder to debug. The solution is to make it more interactive, able to introspect and explain its reasoning. That will take us another step closer to the Master Algorithm.

The doctor will see you now

The cure for cancer is a program that inputs the cancer’s genome and outputs the drug to kill it with. We can now picture what such a program-let’s call it CanceRx-will look like. Despite its outward simplicity, CanceRx is one of the largest and most complex programs ever built-indeed, so large and complex that it could only have been built with the help of machine learning. It is based on a detailed model of how living cells work, with a subclass for each type of cell in the human body and an overarching model of how they interact. This model, in the form of an MLN or something akin to it, combines knowledge of molecular biology with vast amounts of data from DNA sequencers, microarrays, and many other sources. Some of the knowledge was manually encoded, but most was automatically extracted from the biomedical literature. The model is continually evolving, incorporating the results of new experiments, data sources, and patient histories. Ultimately, it will know every pathway, regulatory mechanism, and chemical reaction in every type of human cell-the sum total of human molecular biology.

CanceRx spends most of its time querying the model with candidate drugs. Given a new drug, the model predicts its effect on both cancer cells and normal ones. When Alice is diagnosed with cancer, CanceRx instantiates its model with both her normal cells and the tumor’s and tries all available drugs until it finds one that kills the cancer cells without harming the healthy ones. If it can’t find a drug or combination of drugs that works, it sets about designing one that will, perhaps evolving it from existing ones using hill climbing or crossover. At each step in the search, it tries the candidate drugs on the model. If a drug stops the cancer but still has some harmful side effect, CanceRx tries to tweak it to get rid of the side effect. When Alice’s cancer mutates, it repeats the whole process. Even before the cancer mutates, the model predicts likely mutations, and CanceRx prescribes drugs that will stop them dead in their tracks. In the game of chess between humanity and cancer, CanceRx is checkmate.

Notice that machine learning isn’t going to give us CanceRx all by itself. It’s not as if we have a vast database of molecular biology ready to go, stream it into the Master Algorithm, and out pops the perfect model of a living cell. CanceRx would be the end result, after many iterations, of a worldwide collaboration between hundreds of thousands of biologists, oncologists, and data scientists. Most important, however, CanceRx would incorporate data from millions of cancer patients, with the help of their doctors and hospitals. Without that data, we can’t cure cancer; with it, we can. Contributing to this growing database would not only be in every cancer patient’s interest; it would be her ethical duty. In the world of CanceRx, discrete clinical trials are a thing of the past; new treatments proposed by CanceRx are continually being rolled out, and if they work, given to a widening circle of patients. Both successes and failures provide valuable data for CanceRx’s learning, in a virtuous circle of improvement. If you look at it one way, machine learning is only a small part of the CanceRx project, well behind data gathering and human contributions. But looked at another way, machine learning is the linchpin of the whole enterprise. Without it, we would have only fragmentary knowledge of cancer biology, scattered among thousands of databases and millions of scientific articles, each doctor aware of only a small part. Assembling all this knowledge into a coherent whole is beyond the power of unaided humans, no matter how smart; only machine learning can do it. Because every cancer is different, it takes machine learning to find the common patterns. And because a single tissue can yield billions of data points, it takes machine learning to figure out what to do for each new patient.

The effort to build what will ultimately become CanceRx is already under way. Researchers in the new field of systems biology model whole metabolic networks rather than individual genes and proteins. One group at Stanford has built a model of a whole cell. The Global Alliance for Genomics and Health promotes data sharing among researchers and oncologists, with a view to large-scale analysis. CancerCommons.org assembles cancer models and lets patients pool their histories and learn from similar cases. Foundation Medicine pinpoints the mutations in a patient’s tumor cells and suggests the most appropriate drugs. A decade ago, it wasn’t clear if, or how, cancer would ever be cured. Now we can see how to get there. The road is long, but we have found it.

Оглавление книги