Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER TWO: The Master Algorithm

CHAPTER TWO: The Master Algorithm

Even more astonishing than the breadth of applications of machine learning is that it’s the same algorithms doing all of these different things. Outside of machine learning, if you have two different problems to solve, you need to write two different programs. They might use some of the same infrastructure, like the same programming language or the same database system, but a program to, say, play chess is of no use if you want to process credit-card applications. In machine learning, the same algorithm can do both, provided you give it the appropriate data to learn from. In fact, just a few algorithms are responsible for the great majority of machine-learning applications, and we’ll take a look at them in the next few chapters.

For example, consider Na?ve Bayes, a learning algorithm that can be expressed as a single short equation. Given a database of patient records-their symptoms, test results, and whether or not they had some particular condition-Na?ve Bayes can learn to diagnose the condition in a fraction of a second, often better than doctors who spent many years in medical school. It can also beat medical expert systems that took thousands of person-hours to build. The same algorithm is widely used to learn spam filters, a problem that at first sight has nothing to do with medical diagnosis. Another simple learner, called the nearest-neighbor algorithm, has been used for everything from handwriting recognition to controlling robot hands to recommending books and movies you might like. And decision tree learners are equally apt at deciding whether your credit-card application should be accepted, finding splice junctions in DNA, and choosing the next move in a game of chess.

Not only can the same learning algorithms do an endless variety of different things, but they’re shockingly simple compared to the algorithms they replace. Most learners can be coded up in a few hundred lines, or perhaps a few thousand if you add a lot of bells and whistles. In contrast, the programs they replace can run in the hundreds of thousands or even millions of lines, and a single learner can induce an unlimited number of different programs.

If so few learners can do so much, the logical question is: Could one learner do everything? In other words, could a single algorithm learn all that can be learned from data? This is a very tall order, since it would ultimately include everything in an adult’s brain, everything evolution has created, and the sum total of all scientific knowledge. But in fact all the major learners-including nearest-neighbor, decision trees, and Bayesian networks, a generalization of Na?ve Bayes-are universal in the following sense: if you give the learner enough of the appropriate data, it can approximate any function arbitrarily closely-which is math-speak for learning anything. The catch is that “enough data” could be infinite. Learning from finite data requires making assumptions, as we’ll see, and different learners make different assumptions, which makes them good for some things but not others.

But what if instead of leaving these assumptions embedded in the algorithm we make them an explicit input, along with the data, and allow the user to choose which ones to plug in, perhaps even state new ones? Is there an algorithm that can take in any data and assumptions and output the knowledge that’s implicit in them? I believe so. Of course, we have to put some limits on what the assumptions can be, otherwise we could cheat by giving the algorithm the entire target knowledge, or close to it, in the form of assumptions. But there are many ways to do this, from limiting the size of the input to requiring that the assumptions be no stronger than those of current learners.

The question then becomes: How weak can the assumptions be and still allow all relevant knowledge to be derived from finite data? Notice the word relevant: we’re only interested in knowledge about our world, not about worlds that don’t exist. So inventing a universal learner boils down to discovering the deepest regularities in our universe, those that all phenomena share, and then figuring out a computationally efficient way to combine them with data. This requirement of computational efficiency precludes just using the laws of physics as the regularities, as we’ll see. It does not, however, imply that the universal learner has to be as efficient as more specialized ones. As so often happens in computer science, we’re willing to sacrifice efficiency for generality. This also applies to the amount of data required to learn a given target knowledge: a universal learner will generally need more data than a specialized one, but that’s OK provided we have the necessary amount-and the bigger data gets, the more likely this will be the case.

Here, then, is the central hypothesis of this book:

All knowledge-past, present, and future-can be derived from data by a single, universal learning algorithm.

I call this learner the Master Algorithm. If such an algorithm is possible, inventing it would be one of the greatest scientific achievements of all time. In fact, the Master Algorithm is the last thing we’ll ever have to invent because, once we let it loose, it will go on to invent everything else that can be invented. All we need to do is provide it with enough of the right kind of data, and it will discover the corresponding knowledge. Give it a video stream, and it learns to see. Give it a library, and it learns to read. Give it the results of physics experiments, and it discovers the laws of physics. Give it DNA crystallography data, and it discovers the structure of DNA.

This may sound far-fetched: How could one algorithm possibly learn so many different things and such difficult ones? But in fact many lines of evidence point to the existence of a Master Algorithm. Let’s see what they are.

The argument from neuroscience

In April 2000, a team of neuroscientists from MIT reported in Nature the results of an extraordinary experiment. They rewired the brain of a ferret, rerouting the connections from the eyes to the auditory cortex (the part of the brain responsible for processing sounds) and rerouting the connections from the ears to the visual cortex. You’d think the result would be a severely disabled ferret, but no: the auditory cortex learned to see, the visual cortex learned to hear, and the ferret was fine. In normal mammals, the visual cortex contains a map of the retina: neurons connected to nearby regions of the retina are close to each other in the cortex. Instead, the rewired ferrets developed a map of the retina in the auditory cortex. If the visual input is redirected instead to the somatosensory cortex, responsible for touch perception, it too learns to see. Other mammals also have this ability.

In congenitally blind people, the visual cortex can take over other brain functions. In deaf ones, the auditory cortex does the same. Blind people can learn to “see” with their tongues by sending video images from a head-mounted camera to an array of electrodes placed on the tongue, with high voltages corresponding to bright pixels and low voltages to dark ones. Ben Underwood was a blind kid who taught himself to use echolocation to navigate, like bats do. By clicking his tongue and listening to the echoes, he could walk around without bumping into obstacles, ride a skateboard, and even play basketball. All of this is evidence that the brain uses the same learning algorithm throughout, with the areas dedicated to the different senses distinguished only by the different inputs they are connected to (e.g., eyes, ears, nose). In turn, the associative areas acquire their function by being connected to multiple sensory regions, and the “executive” areas acquire theirs by connecting the associative areas and motor output.

Examining the cortex under a microscope leads to the same conclusion. The same wiring pattern is repeated everywhere. The cortex is organized into columns with six distinct layers, feedback loops running to another brain structure called the thalamus, and a recurring pattern of short-range inhibitory connections and longer-range excitatory ones. A certain amount of variation is present, but it looks more like different parameters or settings of the same algorithm than different algorithms. Low-level sensory areas have more noticeable differences, but as the rewiring experiments show, these are not crucial. The cerebellum, the evolutionarily older part of the brain responsible for low-level motor control, has a clearly different and very regular architecture, built out of much smaller neurons, so it would seem that at least motor learning uses a different algorithm. If someone’s cerebellum is injured, however, the cortex takes over its function. Thus it seems that evolution kept the cerebellum around not because it does something the cortex can’t, but just because it’s more efficient.

The computations taking place within the brain’s architecture are also similar throughout. All information in the brain is represented in the same way, via the electrical firing patterns of neurons. The learning mechanism is also the same: memories are formed by strengthening the connections between neurons that fire together, using a biochemical process known as long-term potentiation. All this is not just true of humans: different animals have similar brains. Ours is unusually large, but seems to be built along the same principles as other animals’.

Another line of argument for the unity of the cortex comes from what might be called the poverty of the genome. The number of connections in your brain is over a million times the number of letters in your genome, so it’s not physically possible for the genome to specify in detail how the brain is wired.

The most important argument for the brain being the Master Algorithm, however, is that it’s responsible for everything we can perceive and imagine. If something exists but the brain can’t learn it, we don’t know it exists. We may just not see it or think it’s random. Either way, if we implement the brain in a computer, that algorithm can learn everything we can. Thus one route-arguably the most popular one-to inventing the Master Algorithm is to reverse engineer the brain. Jeff Hawkins took a stab at this in his book On Intelligence. Ray Kurzweil pins his hopes for the Singularity-the rise of artificial intelligence that greatly exceeds the human variety-on doing just that and takes a stab at it himself in his book How to Create a Mind. Nevertheless, this is only one of several possible approaches, as we’ll see. It’s not even necessarily the most promising one, because the brain is phenomenally complex, and we’re still in the very early stages of deciphering it. On the other hand, if we can’t figure out the Master Algorithm, the Singularity won’t happen any time soon.

Not all neuroscientists believe in the unity of the cortex; we need to learn more before we can be sure. The question of just what the brain can and can’t learn is also hotly debated. But if there’s something we know but the brain can’t learn, it must have been learned by evolution.

The argument from evolution

Life’s infinite variety is the result of a single mechanism: natural selection. Even more remarkable, this mechanism is of a type very familiar to computer scientists: iterative search, where we solve a problem by trying many candidate solutions, selecting and modifying the best ones, and repeating these steps as many times as necessary. Evolution is an algorithm. Paraphrasing Charles Babbage, the Victorian-era computer pioneer, God created not species but the algorithm for creating species. The “endless forms most beautiful” Darwin spoke of in the conclusion of The Origin of Species belie a most beautiful unity: all of those forms are encoded in strings of DNA, and all of them come about by modifying and combining those strings. Who would have guessed, given only a description of this algorithm, that it could produce you and me? If evolution can learn us, it can conceivably also learn everything that can be learned, provided we implement it on a powerful enough computer. Indeed, evolving programs by simulating natural selection is a popular endeavor in machine learning. Evolution, then, is another promising path to the Master Algorithm.

Evolution is the ultimate example of how much a simple learning algorithm can achieve given enough data. Its input is the experience and fate of all living creatures that ever existed. (Now that’s big data.) On the other hand, it’s been running for over three billion years on the most powerful computer on Earth: Earth itself. A computer version of it had better be faster and less data intensive than the original. Which one is the better model for the Master Algorithm: evolution or the brain? This is machine learning’s version of the nature versus nurture debate. And, just as nature and nurture combine to produce us, perhaps the true Master Algorithm contains elements of both.

The argument from physics

In a famous 1959 essay, the physicist and Nobel laureate Eugene Wigner marveled at what he called “the unreasonable effectiveness of mathematics in the natural sciences.” By what miracle do laws induced from scant observations turn out to apply far beyond them? How can the laws be many orders of magnitude more precise than the data they are based on? Most of all, why is it that the simple, abstract language of mathematics can accurately capture so much of our infinitely complex world? Wigner considered this a deep mystery, in equal parts fortunate and unfathomable. Nevertheless, it is so, and the Master Algorithm is a logical extension of it.

If the world were just a blooming, buzzing confusion, there would be reason to doubt the existence of a universal learner. But if everything we experience is the product of a few simple laws, then it makes sense that a single algorithm can induce all that can be induced. All the Master Algorithm has to do is provide a shortcut to the laws’ consequences, replacing impossibly long mathematical derivations with much shorter ones based on actual observations.

For example, we believe that the laws of physics gave rise to evolution, but we don’t know how. Instead, we can induce natural selection directly from observations, as Darwin did. Countless wrong inferences could be drawn from those observations, but most of them never occur to us, because our inferences are influenced by our broad knowledge of the world, and that knowledge is consistent with the laws of nature.

How much of the character of physical law percolates up to higher domains like biology and sociology remains to be seen, but the study of chaos provides many tantalizing examples of very different systems with similar behavior, and the theory of universality explains them. The Mandelbrot set is a beautiful example of how a very simple iterative procedure can give rise to an inexhaustible variety of forms. If the mountains, rivers, clouds, and trees of the world are all the result of such procedures-and fractal geometry shows they are-perhaps those procedures are just different parametrizations of a single one that we can induce from them.

In physics, the same equations applied to different quantities often describe phenomena in completely different fields, like quantum mechanics, electromagnetism, and fluid dynamics. The wave equation, the diffusion equation, Poisson’s equation: once we discover it in one field, we can more readily discover it in others; and once we’ve learned how to solve it in one field, we know how to solve it in all. Moreover, all these equations are quite simple and involve the same few derivatives of quantities with respect to space and time. Quite conceivably, they are all instances of a master equation, and all the Master Algorithm needs to do is figure out how to instantiate it for different data sets.

Another line of evidence comes from optimization, the branch of mathematics concerned with finding the input to a function that produces its highest output. For example, finding the sequence of stock purchases and sales that maximizes your total returns is an optimization problem. In optimization, simple functions often give rise to surprisingly complex solutions. Optimization plays a prominent role in almost every field of science, technology, and business, including machine learning. Each field optimizes within the constraints defined by optimizations in other fields. We try to maximize our happiness within economic constraints, which are firms’ best solutions within the constraints of the available technology-which in turn consists of the best solutions we could find within the constraints of biology and physics. Biology, in turn, is the result of optimization by evolution within the constraints of physics and chemistry, and the laws of physics themselves are solutions to optimization problems. Perhaps, then, everything that exists is the progressive solution of an overarching optimization problem, and the Master Algorithm follows from the statement of that problem.

Physicists and mathematicians are not the only ones who find unexpected connections between disparate fields. In his book Consilience, the distinguished biologist E. O. Wilson makes an impassioned argument for the unity of all knowledge, from science to the humanities. The Master Algorithm is the ultimate expression of this unity: if all knowledge shares a common pattern, the Master Algorithm exists, and vice versa.

Nevertheless, physics is unique in its simplicity. Outside physics and engineering, the track record of mathematics is more mixed. Sometimes it’s only reasonably effective, and sometimes its models are too oversimplified to be useful. This tendency to oversimplify stems from the limitations of the human mind, however, not from the limitations of mathematics. Most of the brain’s hardware (or rather, wetware) is devoted to sensing and moving, and to do math we have to borrow parts of it that evolved for language. Computers have no such limitations and can easily turn big data into very complex models. Machine learning is what you get when the unreasonable effectiveness of mathematics meets the unreasonable effectiveness of data. Biology and sociology will never be as simple as physics, but the method by which we discover their truths can be.

The argument from statistics

According to one school of statisticians, a single simple formula underlies all learning. Bayes’ theorem, as the formula is known, tells you how to update your beliefs whenever you see new evidence. A Bayesian learner starts with a set of hypotheses about the world. When it sees a new piece of data, the hypotheses that are compatible with it become more likely, and the hypotheses that aren’t become less likely (or even impossible). After seeing enough data, a single hypothesis dominates, or a few do. For example, if I’m looking for a program that accurately predicts stock movements and a stock that a candidate program had predicted would go up instead goes down, that candidate loses credibility. After I’ve reviewed a number of candidates, only a few credible ones will remain, and they will encapsulate my new knowledge of the stock market.

Bayes’ theorem is a machine that turns data into knowledge. According to Bayesian statisticians, it’s the only correct way to turn data into knowledge. If they’re right, either Bayes’ theorem is the Master Algorithm or it’s the engine that drives it. Other statisticians have serious reservations about the way Bayes’ theorem is used and prefer different ways to learn from data. In the days before computers, Bayes’ theorem could only be applied to very simple problems, and the idea of it as a universal learner would have seemed far-fetched. With big data and big computing to go with it, however, Bayes can find its way in vast hypothesis spaces and has spread to every conceivable field of knowledge. If there’s a limit to what Bayes can learn, we haven’t found it yet.

The argument from computer science

When I was a senior in college, I wasted a summer playing Tetris, a highly addictive video game where variously shaped pieces fall from above and which you try to pack as closely together as you can; the game is over when the pile of pieces reaches the top of the screen. Little did I know that this was my introduction to NP-completeness, the most important problem in theoretical computer science. Turns out that, far from an idle pursuit, mastering Tetris-really mastering it-is one of the most useful things you could ever do. If you can solve Tetris, you can solve thousands of the hardest and most important problems in science, technology, and management-all in one fell swoop. That’s because at heart they are all the same problem. This is one of the most astonishing facts in all of science.

Figuring out how proteins fold into their characteristic shapes; reconstructing the evolutionary history of a set of species from their DNA; proving theorems in propositional logic; detecting arbitrage opportunities in markets with transaction costs; inferring a three-dimensional shape from two-dimensional views; compressing data on a disk; forming a stable coalition in politics; modeling turbulence in sheared flows; finding the safest portfolio of investments with a given return, the shortest route to visit a set of cities, the best layout of components on a microchip, the best placement of sensors in an ecosystem, or the lowest energy state of a spin glass; scheduling flights, classes, and factory jobs; optimizing resource allocation, urban traffic flow, social welfare, and (most important) your Tetris score: these are all NP-complete problems, meaning that if you can efficiently solve one of them you can efficiently solve all problems in the class NP, including each other. Who would have guessed that all these problems, superficially so different, are really the same? But if they are, it makes sense that one algorithm could learn to solve all of them (or, more precisely, all efficiently solvable instances).

P and NP are the two most important classes of problems in computer science. (The names are not very mnemonic, unfortunately.) A problem is in P if we can solve it efficiently, and it’s in NP if we can efficiently check its solution. The famous P = NP question is whether every efficiently checkable problem is also efficiently solvable. Because of NP-completeness, all it takes to answer it is to prove that one NP-complete problem is efficiently solvable (or not). NP is not the hardest class of problems in computer science, but it’s arguably the hardest “realistic” class: if you can’t even check a problem’s solution before the universe ends, what’s the point of trying to solve it? Humans are good at solving NP problems approximately, and conversely, problems that we find interesting (like Tetris) often have an “NP-ness” about them. One definition of artificial intelligence is that it consists of finding heuristic solutions to NP-complete problems. Often, we do this by reducing them to satisfiability, the canonical NP-complete problem: Can a given logical formula ever be true, or is it self-contradictory? If we invent a learner that can learn to solve satisfiability, it has a good claim to being the Master Algorithm.

NP-completeness aside, the sheer existence of computers is itself a powerful sign that there is a Master Algorithm. If you could travel back in time to the early twentieth century and tell people that a soon-to-be-invented machine would solve problems in every realm of human endeavor-the same machine for every problem-no one would believe you. They would say that each machine can only do one thing: sewing machines don’t type, and typewriters don’t sew. Then in 1936 Alan Turing imagined a curious contraption with a tape and a head that read and wrote symbols on it, now known as a Turing machine. Every conceivable problem that can be solved by logical deduction can be solved by a Turing machine. Furthermore, a so-called universal Turing machine can simulate any other by reading its specification from the tape-in other words, it can be programmed to do anything.

The Master Algorithm is for induction, the process of learning, what the Turing machine is for deduction. It can learn to simulate any other algorithm by reading examples of its input-output behavior. Just as there are many models of computation equivalent to a Turing machine, there are probably many different equivalent formulations of a universal learner. The point, however, is to find the first such formulation, just as Turing found the first formulation of the general-purpose computer.

Machine learners versus knowledge engineers

Of course, the Master Algorithm has at least as many skeptics as it has proponents. Doubt is in order when something looks like a silver bullet. The most determined resistance comes from machine learning’s perennial foe: knowledge engineering. According to its proponents, knowledge can’t be learned automatically; it must be programmed into the computer by human experts. Sure, learners can extract some things from data, but nothing you’d confuse with real knowledge. To knowledge engineers, big data is not the new oil; it’s the new snake oil.

In the early days of AI, machine learning seemed like the obvious path to computers with humanlike intelligence; Turing and others thought it was the only plausible path. But then the knowledge engineers struck back, and by 1970 machine learning was firmly on the back burner. For a moment in the 1980s, it seemed like knowledge engineering was about to take over the world, with companies and countries making massive investments in it. But disappointment soon set in, and machine learning began its inexorable rise, at first quietly, and then riding a roaring wave of data.

Despite machine learning’s successes, the knowledge engineers remain unconvinced. They believe that its limitations will soon become apparent, and the pendulum will swing back. Marvin Minsky, an MIT professor and AI pioneer, is a prominent member of this camp. Minsky is not just skeptical of machine learning as an alternative to knowledge engineering, he’s skeptical of any unifying ideas in AI. Minsky’s theory of intelligence, as expressed in his book The Society of Mind, could be unkindly characterized as “the mind is just one damn thing after another.” The Society of Mind is a laundry list of hundreds of separate ideas, each with its own vignette. The problem with this approach to AI is that it doesn’t work; it’s stamp collecting by computer. Without machine learning, the number of ideas needed to build an intelligent agent is infinite. If a robot had all the same capabilities as a human except learning, the human would soon leave it in the dust.

Minsky was an ardent supporter of the Cyc project, the most notorious failure in the history of AI. The goal of Cyc was to solve AI by entering into a computer all the necessary knowledge. When the project began in the 1980s, its leader, Doug Lenat, confidently predicted success within a decade. Thirty years later, Cyc continues to grow without end in sight, and commonsense reasoning still eludes it. Ironically, Lenat has belatedly embraced populating Cyc by mining the web, not because Cyc can read, but because there’s no other way.

Even if by some miracle we managed to finish coding up all the necessary pieces, our troubles would be just beginning. Over the years, a number of research groups have attempted to build complete intelligent agents by putting together algorithms for vision, speech recognition, language understanding, reasoning, planning, navigation, manipulation, and so on. Without a unifying framework, these attempts soon hit an insurmountable wall of complexity: too many moving parts, too many interactions, too many bugs for poor human software engineers to cope with. Knowledge engineers believe AI is just an engineering problem, but we have not yet reached the point where engineering can take us the rest of the way. In 1962, when Kennedy gave his famous moon-shot speech, going to the moon was an engineering problem. In 1662, it wasn’t, and that’s closer to where AI is today.

In industry, there’s no sign that knowledge engineering will ever be able to compete with machine learning outside of a few niche areas. Why pay experts to slowly and painfully encode knowledge into a form computers can understand, when you can extract it from data at a fraction of the cost? What about all the things the experts don’t know but you can discover from data? And when data is not available, the cost of knowledge engineering seldom exceeds the benefit. Imagine if farmers had to engineer each cornstalk in turn, instead of sowing the seeds and letting them grow: we would all starve.

Another prominent machine-learning skeptic is the linguist Noam Chomsky. Chomsky believes that language must be innate, because the examples of grammatical sentences children hear are not enough to learn a grammar. This only puts the burden of learning language on evolution, however; it does not argue against the Master Algorithm but only against it being something like the brain. Moreover, if a universal grammar exists (as Chomsky believes), elucidating it is a step toward elucidating the Master Algorithm. The only way this is not the case is if language has nothing in common with other cognitive abilities, which is implausible given its evolutionary recency.

In any case, if we formalize Chomsky’s “poverty of the stimulus” argument, we find that it’s demonstrably false. In 1969, J. J. Horning proved that probabilistic context-free grammars can be learned from positive examples only, and stronger results have followed. (Context-free grammars are the linguist’s bread and butter, and the probabilistic version models how likely each rule is to be used.) Besides, language learning doesn’t happen in a vacuum; children get all sorts of cues from their parents and the environment. If we’re able to learn language from a few years’ worth of examples, it’s partly because of the similarity between its structure and the structure of the world. This common structure is what we’re interested in, and we know from Horning and others that it suffices.

More generally, Chomsky is critical of all statistical learning. He has a list of things statistical learners can’t do, but the list is fifty years out of date. Chomsky seems to equate machine learning with behaviorism, where animal behavior is reduced to associating responses with rewards. But machine learning is not behaviorism. Modern learning algorithms can learn rich internal representations, not just pairwise associations between stimuli.

In the end, the proof is in the pudding. Statistical language learners work, and hand-engineered language systems don’t. The first eye-opener came in the 1970s, when DARPA, the Pentagon’s research arm, organized the first large-scale speech recognition project. To everyone’s surprise, a simple sequential learner of the type Chomsky derided handily beat a sophisticated knowledge-based system. Learners like it are now used in just about every speech recognizer, including Siri. Fred Jelinek, head of the speech group at IBM, famously quipped that “every time I fire a linguist, the recognizer’s performance goes up.” Stuck in the knowledge-engineering mire, computational linguistics had a near-death experience in the late 1980s. Since then, learning-based methods have swept the field, to the point where it’s hard to find a paper devoid of learning in a computational linguistics conference. Statistical parsers analyze language with accuracy close to that of humans, where hand-coded ones lagged far behind. Machine translation, spelling correction, part-of-speech tagging, word sense disambiguation, question answering, dialogue, summarization: the best systems in these areas all use learning. Watson, the Jeopardy! computer champion, would not have been possible without it.

To this Chomsky might reply that engineering successes are not proof of scientific validity. On the other hand, if your buildings collapse and your engines don’t run, perhaps something is wrong with your theory of physics. Chomsky thinks linguists should focus on “ideal” speaker-listeners, as defined by him, and this gives him license to ignore things like the need for statistics in language learning. Perhaps it’s not surprising, then, that few experimentalists take his theories seriously any more.

Another potential source of objections to the Master Algorithm is the notion, popularized by the psychologist Jerry Fodor, that the mind is composed of a set of modules with only limited communication between them. For example, when you watch TV your “higher brain” knows that it’s only light flickering on a flat surface, but your visual system still sees three-dimensional shapes. Even if we believe in the modularity of mind, however, that does not imply that different modules use different learning algorithms. The same algorithm operating on, say, visual and verbal information may suffice.

Critics like Minsky, Chomsky, and Fodor once had the upper hand, but thankfully their influence has waned. Nevertheless, we should keep their criticisms in mind as we set out on the road to the Master Algorithm for two reasons. The first is that knowledge engineers faced many of the same problems machine learners do, and even if they didn’t succeed, they learned many valuable lessons. The second is that learning and knowledge are intertwined in surprisingly subtle ways, as we’ll soon find out. Unfortunately, the two camps often talk past each other. They speak different languages: machine learning speaks probability, and knowledge engineering speaks logic. Later in the book we’ll see what to do about this.

Swan bites robot

“No matter how smart your algorithm, there are some things it just can’t learn.” Outside of AI and cognitive science, the most common objections to machine learning are variants of this claim. Nassim Taleb hammered on it forcefully in his book The Black Swan. Some events are simply not predictable. If you’ve only ever seen white swans, you think the probability of ever seeing a black one is zero. The financial meltdown of 2008 was a “black swan.”

It’s true that some things are predictable and some aren’t, and the first duty of the machine learner is to distinguish between them. But the goal of the Master Algorithm is to learn everything that can be known, and that’s a vastly wider domain than Taleb and others imagine. The housing bust was far from a black swan; on the contrary, it was widely predicted. Most banks’ models failed to see it coming, but that was due to well-understood limitations of those models, not limitations of machine learning in general. Learning algorithms are quite capable of accurately predicting rare, never-before-seen events; you could even say that that’s what machine learning is all about. What’s the probability of a black swan if you’ve never seen one? How about it’s the fraction of known species that belatedly turned out to have black specimens? This is only a crude example; we’ll see many deeper ones in this book.

A related, frequently heard objection is “Data can’t replace human intuition.” In fact, it’s the other way around: human intuition can’t replace data. Intuition is what you use when you don’t know the facts, and since you often don’t, intuition is precious. But when the evidence is before you, why would you deny it? Statistical analysis beats talent scouts in baseball (as Michael Lewis memorably documented in Moneyball), it beats connoisseurs at wine tasting, and every day we see new examples of what it can do. Because of the influx of data, the boundary between evidence and intuition is shifting rapidly, and as with any revolution, entrenched ways have to be overcome. If I’m the expert on X at company Y, I don’t like to be overridden by some guy with data. There’s a saying in industry: “Listen to your customers, not to the HiPPO,” HiPPO being short for “highest paid person’s opinion.” If you want to be tomorrow’s authority, ride the data, don’t fight it.

OK, some say, machine learning can find statistical regularities in data, but it will never discover anything deep, like Newton’s laws. It arguably hasn’t yet, but I bet it will. Stories of falling apples notwithstanding, deep scientific truths are not low-hanging fruit. Science goes through three phases, which we can call the Brahe, Kepler, and Newton phases. In the Brahe phase, we gather lots of data, like Tycho Brahe patiently recording the positions of the planets night after night, year after year. In the Kepler phase, we fit empirical laws to the data, like Kepler did to the planets’ motions. In the Newton phase, we discover the deeper truths. Most science consists of Brahe- and Kepler-like work; Newton moments are rare. Today, big data does the work of billions of Brahes, and machine learning the work of millions of Keplers. If-let’s hope so-there are more Newton moments to be had, they are as likely to come from tomorrow’s learning algorithms as from tomorrow’s even more overwhelmed scientists, or at least from a combination of the two. (Of course, the Nobel prizes will go to the scientists, whether they have the key insights or just push the button. Learning algorithms have no ambitions of their own.) We’ll see in this book what those algorithms might look like and speculate about what they might discover-such as a cure for cancer.

Is the Master Algorithm a fox or a hedgehog?

We need to consider one more potential objection to the Master Algorithm, perhaps the most serious one of all. It comes not from knowledge engineers or disgruntled experts, but from the machine-learning practitioners themselves. Putting that hat on for a moment, I might say: “But the Master Algorithm does not look like my daily life. I try hundreds of variations of many different learning algorithms on any given problem, and different algorithms do better on different problems. How could a single algorithm replace them all?”

To which the answer is: indeed. Wouldn’t it be nice if, instead of trying hundreds of variations of many algorithms, we just had to try hundreds of variations of a single one? If we can figure out what’s important and not so important in each one, what the important parts have in common and how they complement each other, we can, indeed, synthesize a Master Algorithm from them. That’s what we’re going to do in this book, or as close to it as we can. Perhaps you, dear reader, will have some ideas of your own as you read it.

How complex will the Master Algorithm be? Thousands of lines of code? Millions? We don’t know yet, but machine learning has a delightful history of simple algorithms unexpectedly beating very fancy ones. In a famous passage of his book The Sciences of the Artificial, AI pioneer and Nobel laureate Herbert Simon asked us to consider an ant laboriously making its way home across a beach. The ant’s path is complex, not because the ant itself is complex but because the environment is full of dunelets to climb and pebbles to get around. If we tried to model the ant by programming in every possible path, we’d be doomed. Similarly, in machine learning the complexity is in the data; all the Master Algorithm has to do is assimilate it, so we shouldn’t be surprised if it turns out to be simple. The human hand is simple-four fingers, one opposable thumb-and yet it can make and use an infinite variety of tools. The Master Algorithm is to algorithms what the hand is to pens, swords, screwdrivers, and forks.

As Isaiah Berlin memorably noted, some thinkers are foxes-they know many small things-and some are hedgehogs-they know one big thing. The same is true of learning algorithms. I hope the Master Algorithm is a hedgehog, but even if it’s a fox, we can’t catch it soon enough. The biggest problem with today’s learning algorithms is not that they are plural; it’s that, useful as they are, they still don’t do everything we’d like them to. Before we can discover deep truths with machine learning, we have to discover deep truths about machine learning.

What’s at stake

Suppose you’ve been diagnosed with cancer, and the traditional treatments-surgery, chemotherapy, and radiation therapy-have failed. What happens next will determine whether you live or die. The first step is to get the tumor’s genome sequenced. Companies like Foundation Medicine in Cambridge, Massachusetts, will do that for you: send them a sample of the tumor and they will send back a list of the known cancer-related mutations in its genome. This is needed because every cancer is different, and no single drug is likely to work for all. Cancers mutate as they spread through your body, and by natural selection, the mutations most resistant to the drugs you’re taking are the most likely to grow. The right drug for you may be one that works for only 5 percent of patients, or you may need a combination of drugs that has never been tried before. Perhaps it will take a new drug designed specifically for your cancer, or a sequence of drugs to parry the cancer’s adaptations. Yet these drugs may have side effects that are deadly for you but not most other people. No doctor can keep track of all the information needed to predict the best treatment for you, given your medical history and your cancer’s genome. It’s an ideal job for machine learning, and yet today’s learners aren’t up to it. Each has some of the needed capabilities but is missing others. The Master Algorithm is the complete package. Applying it to vast amounts of patient and drug data, combined with knowledge mined from the biomedical literature, is how we will cure cancer.

A universal learner is sorely needed in many other areas, from life-and-death to mundane situations. Picture the ideal recommender system, one that recommends the books, movies, and gadgets you would pick for yourself if you had the time to check them all out. Amazon’s algorithm is a very far cry from it. That’s partly because it doesn’t have enough data-mainly it just knows which items you previously bought from Amazon-but if you went hog wild and gave it access to your complete stream of consciousness from birth, it wouldn’t know what to do with it. How do you transmute the kaleidoscope of your life, the myriad different choices you’ve made, into a coherent picture of who you are and what you want? This is well beyond the ken of today’s learners, but given enough data, the Master Algorithm should be able to understand you roughly as well as your best friend.

Someday there’ll be a robot in every house, doing the dishes, making the beds, even looking after the children while the parents work. How soon depends on how hard finding the Master Algorithm turns out to be. If the best we can do is combine many different learners, each of which solves only a small part of the AI problem, we’ll soon run into the complexity wall. This piecemeal approach worked for Jeopardy!, but few believe tomorrow’s housebots will be Watson’s grandchildren. It’s not that the Master Algorithm will single-handedly crack AI; there’ll still be great feats of engineering to perform, and Watson is a good preview of them. But the 80/20 rule applies: the Master Algorithm will be 80 percent of the solution and 20 percent of the work, so it’s surely the best place to start.

The Master Algorithm’s impact on technology will not be limited to AI. A universal learner is a phenomenal weapon against the complexity monster. Systems that today are too complex to build will no longer be. Computers will do more with less help from us. They will not repeat the same mistakes over and over again, but learn with practice, like people do. Sometimes, like the butlers of legend, they’ll even guess what we want before we express it. If computers make us smarter, computers running the Master Algorithm will make us feel like geniuses. Technological progress will noticeably speed up, not just in computer science but in many different fields. This in turn will add to economic growth and speed poverty’s decline. With the Master Algorithm to help synthesize and distribute knowledge, the intelligence of an organization will be more than the sum of its parts, not less. Routine jobs will be automated and replaced by more interesting ones. Every job will be done better than it is today, whether by a better-trained human, a computer, or a combination of the two. Stock-market crashes will be fewer and smaller. With a fine grid of sensors covering the globe and learned models to make sense of its output moment by moment, we will no longer be flying blind; the health of our planet will take a turn for the better. A model of you will negotiate the world on your behalf, playing elaborate games with other people’s and entities’ models. And as a result of all this, our lives will be longer, happier, and more productive.

Because the potential impact is so great, it would behoove us to try to invent the Master Algorithm even if the odds of success were low. And even if it takes a long time, searching for a universal learner has many immediate benefits. One is the better understanding of machine learning that a unified view enables. Too many business decisions are made with scant understanding of the analytics underpinning them, but it doesn’t have to be that way. To use a technology, we don’t need to master its inner workings, but we do need to have a good conceptual model of it. We need to know how to find a station on the radio, or change the volume. Today, those of us who aren’t machine-learning experts have no conceptual model of what a learner does. The algorithms we drive when we use Google, Facebook, or the latest analytics suite are a bit like a black limo with tinted windows that mysteriously shows up at our door one night: Should we get in? Where will it take us? It’s time to get in the driver’s seat. Knowing the assumptions that different learners make will help us pick the right one for the job, instead of going with a random one that fell into our lap-and then suffering with it for years, painfully rediscovering what we should have known from the start. By knowing what learners optimize, we can make certain they optimize what we care about, rather than what came in the box. Perhaps most important, once we know how a particular learner arrives at its conclusions, we’ll know what to make of that information-what to believe, what to return to the manufacturer, and how to get a better result next time around. And with the universal learner we’ll develop in this book as the conceptual model, we can do all this without cognitive overload. Machine learning is simple at heart; we just need to peel away the layers of math and jargon to reveal the innermost Russian doll.

These benefits apply in both our personal and professional lives. How do I make the best of the trail of data that my every step in the modern world leaves? Every transaction works on two levels: what it accomplishes for you and what it teaches the system you just interacted with. Being aware of this is the first step to a happy life in the twenty-first century. Teach the learners, and they will serve you; but first you need to understand them. What in my job can be done by a learning algorithm, what can’t, and-most important-how can I take advantage of machine learning to do it better? The computer is your tool, not your adversary. Armed with machine learning, a manager becomes a supermanager, a scientist a superscientist, an engineer a superengineer. The future belongs to those who understand at a very deep level how to combine their unique expertise with what algorithms do best.

But perhaps the Master Algorithm is a Pandora’s box best left closed. Will computers enslave us or even exterminate us? Will machine learning be the handmaiden of dictators or evil corporations? Knowing where machine learning is headed will help us to understand what to worry about, what not, and what to do about it. The Terminator scenario, where a super-AI becomes sentient and subdues mankind with a robot army, has no chance of coming to pass with the kinds of learning algorithms we’ll meet in this book. Just because computers can learn doesn’t mean they magically acquire a will of their own. Learners learn to achieve the goals we set them; they don’t get to change the goals. Rather, we need to worry about them trying to serve us in ways that do more harm than good because they don’t know any better, and the cure for that is to teach them better.

Most of all, we have to worry about what the Master Algorithm could do in the wrong hands. The first line of defense is to make sure the good guys get it first-or, if it’s not clear who the good guys are, to make sure it’s open-sourced. The second is to realize that, no matter how good the learning algorithm is, it’s only as good as the data it gets. He who controls the data controls the learner. Your reaction to the datafication of life should not be to retreat to a log cabin-the woods, too, are full of sensors-but to aggressively seek control of the data that matters to you. It’s good to have recommenders that find what you want and bring it to you; you’d feel lost without them. But they should bring you what you want, not what someone else wants you to have. Control of data and ownership of the models learned from it is what many of the twenty-first century’s battles will be about-between governments, corporations, unions, and individuals. But you also have an ethical duty to share data for the common good. Machine learning alone will not cure cancer; cancer patients will, by sharing their data for the benefit of future patients.

A different theory of everything

Science today is thoroughly balkanized, a Tower of Babel where each subcommunity speaks its own jargon and can see only into a few adjacent subcommunities. The Master Algorithm would provide a unifying view of all of science and potentially lead to a new theory of everything. At first this may seem like an odd claim. What machine learning does is induce theories from data. How could the Master Algorithm itself grow into a theory? Isn’t string theory the theory of everything, and the Master Algorithm nothing like it?

To answer these questions, we have to first understand what a scientific theory is and is not. A theory is a set of constraints on what the world could be, not a complete description of it. To obtain the latter, you have to combine the theory with data. For example, consider Newton’s second law. It says that force equals mass times acceleration, or F = ma. It does not say what the mass or acceleration of any object are, or the forces acting on it. It only requires that, if the mass of an object is m and its acceleration is a, then the total force on it must be ma. It removes some of the universe’s degrees of freedom, but not all. The same is true of all other physical theories, including relativity, quantum mechanics, and string theory, which are, in effect, refinements of Newton’s laws.

The power of a theory lies in how much it simplifies our description of the world. Armed with Newton’s laws, we only need to know the masses, positions, and velocities of all objects at one point in time; their positions and velocities at all times follow. So Newton’s laws reduce our description of the world by a factor of the number of distinguishable instants in the history of the universe, past and future. Pretty amazing! Of course, Newton’s laws are only an approximation of the true laws of physics, so let’s replace them with string theory, ignoring all its problems and the question of whether it can ever be empirically validated. Can we do better? Yes, for two reasons.

The first is that, in reality, we never have enough data to completely determine the world. Even ignoring the uncertainty principle, precisely knowing the positions and velocities of all particles in the world at some point in time is not remotely feasible. And because the laws of physics are chaotic, uncertainty compounds over time, and pretty soon they determine very little indeed. To accurately describe the world, we need a fresh batch of data at regular intervals. In effect, the laws of physics only tell us what happens locally. This drastically reduces their power.

The second problem is that, even if we had complete knowledge of the world at some point in time, the laws of physics would still not allow us to determine its past and future. This is because the sheer amount of computation required to make those predictions would be beyond the capabilities of any imaginable computer. In effect, to perfectly simulate the universe we would need another, identical universe. This is why string theory is mostly irrelevant outside of physics. The theories we have in biology, psychology, sociology, or economics are not corollaries of the laws of physics; they had to be created from scratch. We assume that they are approximations of what the laws of physics would predict when applied at the scale of cells, brains, and societies, but there’s no way to know.

Unlike the theories of a given field, which only have power within that field, the Master Algorithm has power across all fields. Within field X, it has less power than field X’s prevailing theory, but across all fields-when we consider the whole world-it has vastly more power than any other theory. The Master Algorithm is the germ of every theory; all we need to add to it to obtain theory X is the minimum amount of data required to induce it. (In the case of physics, that would be just the results of perhaps a few hundred key experiments.) The upshot is that, pound for pound, the Master Algorithm may well be the best starting point for a theory of everything we’ll ever have. Pace Stephen Hawking, it may ultimately tell us more about the mind of God than string theory.

Some may say that seeking a universal learner is the epitome of techno-hubris. But dreaming is not hubris. Maybe the Master Algorithm will take its place among the great chimeras, alongside the philosopher’s stone and the perpetual motion machine. Or perhaps it will be more like finding the longitude at sea, given up as too difficult until a lone genius solved it. More likely, it will be the work of generations, raised stone by stone like a cathedral. The only way to find out is to get up early one day and set out on the journey.

Candidates that don’t make the cut

So, if the Master Algorithm exists, what is it? A seemingly obvious candidate is memorization: just remember everything you’ve seen; after a while you’ll have seen everything there is to see, and therefore know everything there is to know. The problem with this is that, as Heraclitus said, you never step in the same river twice. There’s far more to see than you ever could. No matter how many snowflakes you’ve examined, the next one will be different. Even if you had been present at the Big Bang and everywhere since, you would still have seen only a tiny fraction of what you could see in the future. If you had witnessed life on Earth up to ten thousand years ago, that would not have prepared you for what was to come. Someone who grew up in one city doesn’t become paralyzed when they move to another, but a robot capable only of memorization would. Besides, knowledge is not just a long list of facts. Knowledge is general, and has structure. “All humans are mortal” is much more succinct than seven billion statements of mortality, one for each human. Memorization gives us none of these things.

Another candidate Master Algorithm is the microprocessor. After all, the one in your computer can be viewed as a single algorithm whose job is to execute other algorithms, like a universal Turing machine; and it can run any imaginable algorithm, up to its limits of memory and speed. In effect, to a microprocessor an algorithm is just another kind of data. The problem here is that, by itself, the microprocessor doesn’t know how to do anything; it just sits there idle all day. Where do the algorithms it runs come from? If they were coded up by a human programmer, no learning is involved. Nevertheless, there’s a sense in which the microprocessor is a good analog for the Master Algorithm. A microprocessor is not the best hardware for running any particular algorithm. That would be an ASIC (application-specific integrated circuit) designed very precisely for that algorithm. Yet microprocessors are what we use for almost all applications, because their flexibility trumps their relative inefficiency. If we had to build an ASIC for every new application, the Information Revolution would never have happened. Similarly, the Master Algorithm is not the best algorithm for learning any particular piece of knowledge; that would be an algorithm that already encodes most of that knowledge (or all of it, making the data superfluous). The point, however, is to induce the knowledge from data, because it’s easier and costs less; so the more general the learning algorithm, the better.

An even more extreme candidate is the humble NOR gate: a logic switch whose output is 1 only if its inputs are both 0. Recall that all computers are made of logic gates built out of transistors, and all computations can be reduced to combinations of AND, OR, and NOT gates. A NOR gate is just an OR gate followed by a NOT gate: the negation of a disjunction, as in “I’m happy as long as I’m not starving or sick.” AND, OR and NOT can all be implemented using NOR gates, so NOR can do everything, and in fact it’s all some microprocessors use. So why can’t it be the Master Algorithm? It’s certainly unbeatable for simplicity. Unfortunately, a NOR gate is not the Master Algorithm any more than a Lego brick is the universal toy. It can certainly be a universal building block for toys, but a pile of Legos doesn’t spontaneously assemble itself into a toy. The same applies to other simple computation schemes, like Petri nets or cellular automata.

Moving on to more sophisticated alternatives, what about the queries that any good database engine can answer, or the simple algorithms in a statistical package? Aren’t those enough? These are bigger Lego bricks, but they’re still only bricks. A database engine never discovers anything new; it just tells you what it knows. Even if all the humans in a database are mortal, it doesn’t occur to it to generalize mortality to other humans. (Database engineers would blanch at the thought.) Much of statistics is about testing hypotheses, but someone has to formulate them in the first place. Statistical packages can do linear regression and other simple procedures, but these have a very low limit on what they can learn, no matter how much data you feed them. The better packages cross into the gray zone between statistics and machine learning, but there are still many kinds of knowledge they can’t discover.

OK, it’s time to come clean: the Master Algorithm is the equation U(X) = 0. Not only does it fit on a T-shirt; it fits on a postage stamp. Huh? U(X) = 0 just says that some (possibly very complex) function U of some (possibly very complex) variable X is equal to 0. Every equation can be reduced to this form; for example, F = ma is equivalent to F – ma = 0, so if you think of F – ma as a function U of F, voil?: U(F) = 0. In general, X could be any input and U could be any algorithm, so surely the Master Algorithm can’t be any more general than this; and since we’re looking for the most general algorithm we can find, this must be it. I’m just kidding, of course, but this particular failed candidate points to a real danger in machine learning: coming up with a learner that’s so general, it doesn’t have enough content to be useful.

So what’s the least content a learner can have in order to be useful? How about the laws of physics? After all, everything in the world obeys them (we believe), and they gave rise to evolution and (through it) the brain. Well, perhaps the Master Algorithm is implicit in the laws of physics, but if so, then we need to make it explicit. Just throwing data at the laws of physics won’t result in any new laws. Here’s one way to think about it: perhaps some field’s master theory is just the laws of physics compiled into a more convenient form for that field, but if so then we need an algorithm that finds a shortcut from that field’s data to its theory, and it’s not clear the laws of physics can be of any help with this. Another issue is that, if the laws of physics were different, the Master Algorithm would presumably still be able to discover them in many cases. Mathematicians like to say that God can disobey the laws of physics, but even he cannot defy the laws of logic. This may be so, but the laws of logic are for deduction; what we need is something equivalent, but for induction.

The five tribes of machine learning

Of course, we don’t have to start from scratch in our hunt for the Master Algorithm. We have a few decades of machine learning research to draw on. Some of the smartest people on the planet have devoted their lives to inventing learning algorithms, and some would even claim that they already have a universal learner in hand. We will stand on the shoulders of these giants, but take such claims with a grain of salt. Which raises the question: how will we know when we’ve found the Master Algorithm? When the same learner, with only parameter changes and minimal input aside from the data, can understand video and text as well as humans, and make significant new discoveries in biology, sociology, and other sciences. Clearly, by this standard no learner has yet been demonstrated to be the Master Algorithm, even in the unlikely case one already exists.

Crucially, the Master Algorithm is not required to start from scratch in each new problem. That bar is probably too high for any learner to meet, and it’s certainly very unlike what people do. For example, language does not exist in a vacuum; we couldn’t understand a sentence without our knowledge of the world it refers to. Thus, when learning to read, the Master Algorithm can rely on having previously learned to see, hear, and control a robot. Likewise, a scientist does not just blindly fit models to data; he can bring all his knowledge of the field to bear on the problem. Therefore, when making discoveries in biology, the Master Algorithm can first read all the biology it wants, relying on having previously learned to read. The Master Algorithm is not just a passive consumer of data; it can interact with its environment and actively seek the data it wants, like Adam, the robot scientist, or like any child exploring her world.

Our search for the Master Algorithm is complicated, but also enlivened, by the rival schools of thought that exist within machine learning. The main ones are the symbolists, connectionists, evolutionaries, Bayesians, and analogizers. Each tribe has a set of core beliefs, and a particular problem that it cares most about. It has found a solution to that problem, based on ideas from its allied fields of science, and it has a master algorithm that embodies it.

For symbolists, all intelligence can be reduced to manipulating symbols, in the same way that a mathematician solves equations by replacing expressions by other expressions. Symbolists understand that you can’t learn from scratch: you need some initial knowledge to go with the data. They’ve figured out how to incorporate preexisting knowledge into learning, and how to combine different pieces of knowledge on the fly in order to solve new problems. Their master algorithm is inverse deduction, which figures out what knowledge is missing in order to make a deduction go through, and then makes it as general as possible.

For connectionists, learning is what the brain does, and so what we need to do is reverse engineer it. The brain learns by adjusting the strengths of connections between neurons, and the crucial problem is figuring out which connections are to blame for which errors and changing them accordingly. The connectionists’ master algorithm is backpropagation, which compares a system’s output with the desired one and then successively changes the connections in layer after layer of neurons so as to bring the output closer to what it should be.

Evolutionaries believe that the mother of all learning is natural selection. If it made us, it can make anything, and all we need to do is simulate it on the computer. The key problem that evolutionaries solve is learning structure: not just adjusting parameters, like backpropagation does, but creating the brain that those adjustments can then fine-tune. The evolutionaries’ master algorithm is genetic programming, which mates and evolves computer programs in the same way that nature mates and evolves organisms.

Bayesians are concerned above all with uncertainty. All learned knowledge is uncertain, and learning itself is a form of uncertain inference. The problem then becomes how to deal with noisy, incomplete, and even contradictory information without falling apart. The solution is probabilistic inference, and the master algorithm is Bayes’ theorem and its derivates. Bayes’ theorem tells us how to incorporate new evidence into our beliefs, and probabilistic inference algorithms do that as efficiently as possible.

For analogizers, the key to learning is recognizing similarities between situations and thereby inferring other similarities. If two patients have similar symptoms, perhaps they have the same disease. The key problem is judging how similar two things are. The analogizers’ master algorithm is the support vector machine, which figures out which experiences to remember and how to combine them to make new predictions.

Each tribe’s solution to its central problem is a brilliant, hard-won advance. But the true Master Algorithm must solve all five problems, not just one. For example, to cure cancer we need to understand the metabolic networks in the cell: which genes regulate which others, which chemical reactions the resulting proteins control, and how adding a new molecule to the mix would affect the network. It would be silly to try to learn all of this from scratch, ignoring all the knowledge that biologists have painstakingly accumulated over the decades. Symbolists know how to combine this knowledge with data from DNA sequencers, gene expression microarrays, and so on, to produce results that you couldn’t get with either alone. But the knowledge we obtain by inverse deduction is purely qualitative; we need to learn not just who interacts with whom, but how much, and backpropagation can do that. Nevertheless, both inverse deduction and backpropagation would be lost in space without some basic structure on which to hang the interactions and parameters they find, and genetic programming can discover it. At this point, if we had complete knowledge of the metabolism and all the data relevant to a given patient, we could figure out a treatment for her. But in reality the information we have is always very incomplete, and even incorrect in places; we need to make headway despite that, and that’s what probabilistic inference is for. In the hardest cases, the patient’s cancer looks very different from previous ones, and all our learned knowledge fails. Similarity-based algorithms can save the day by seeing analogies between superficially very different situations, zeroing in on their essential similarities and ignoring the rest.

In this book we will synthesize a single algorithm will all these capabilities:

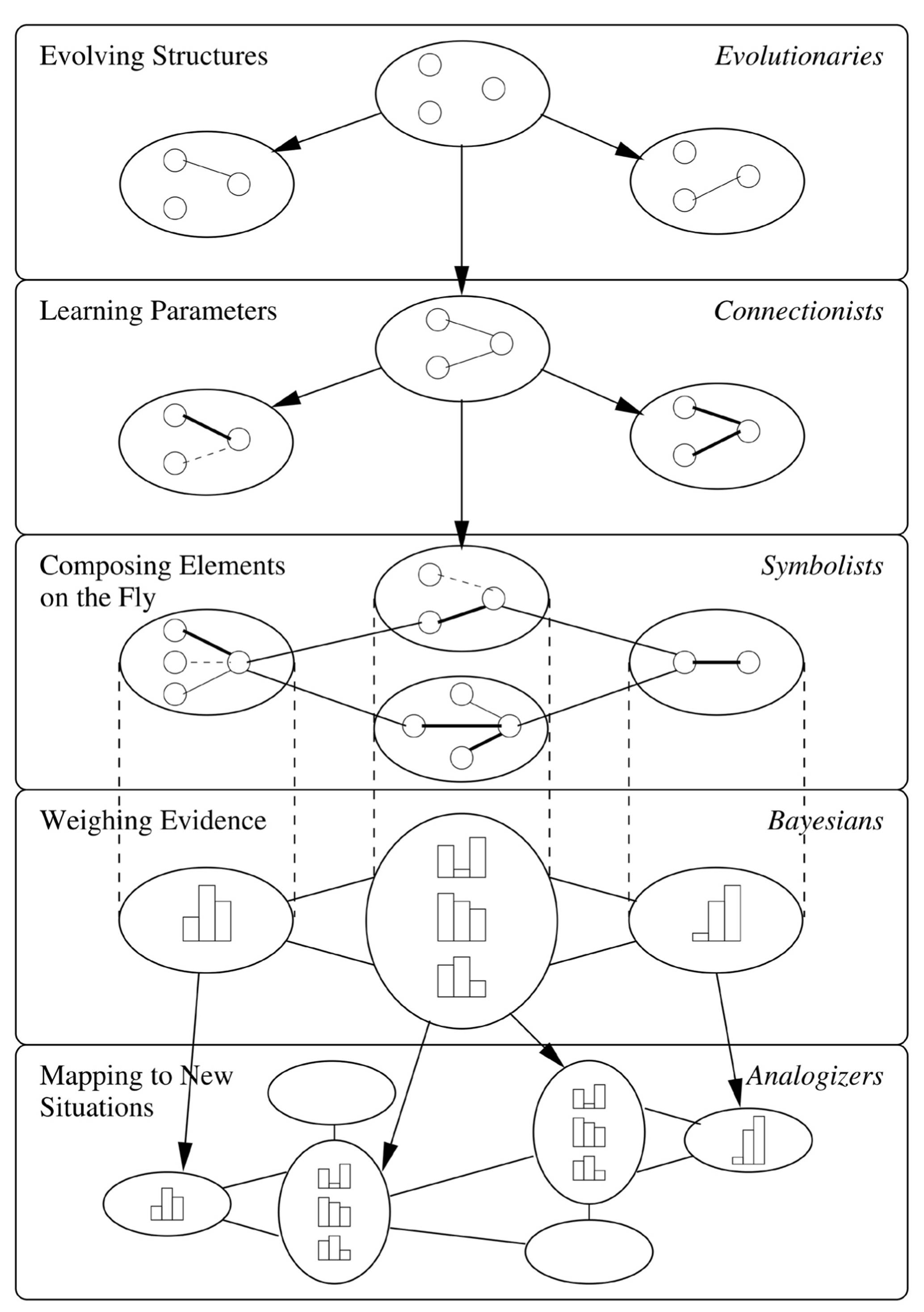
Our quest will take us across the territory of each of the five tribes. The border crossings, where they meet, negotiate and skirmish, will be the trickiest part of the journey. Each tribe has a different piece of the puzzle, which we must gather. Machine learners, like all scientists, resemble the blind men and the elephant: one feels the trunk and thinks it’s a snake, another leans against the leg and thinks it’s a tree, yet another touches the tusk and thinks it’s a bull. Our aim is to touch each part without jumping to conclusions; and once we’ve touched all of them, we will try to picture the whole elephant. It’s far from obvious how to combine all the pieces into one solution-impossible, according to some-but this is what we will do.

The algorithm we’ll arrive at is not yet the Master Algorithm, for reasons we’ll see, but it’s the closest anyone has come. And we’ll gather enough riches along the way to make Croesus envious. Nevertheless, this book is only part one of the Master Algorithm saga. Part two’s protagonist is you, dear reader. Your mission, should you choose to accept it, is to go the rest of the way and bring back the prize. I will be your humble guide in part one, from here to the edge of the known world. Do I hear you protest that you don’t know enough, or algorithms are not your forte? Fear not. Computer science is still young, and unlike in physics or biology, you don’t need a PhD to start a revolution. (Just ask Bill Gates, Messrs. Sergey Brin and Larry Page, or Mark Zuckerberg.) Insight and persistence are what counts.

Are you ready? Our journey begins with a visit to the symbolists, the tribe with the oldest roots.

Оглавление книги