Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER FIVE: Evolution: Nature’s Learning Algorithm

CHAPTER FIVE: Evolution: Nature’s Learning Algorithm

Robotic Park is a massive robot factory surrounded by ten thousand square miles of jungle, urban and otherwise. Ringing that jungle is the tallest, thickest wall ever built, bristling with sentry posts, searchlights, and gun turrets. The wall has two purposes: to keep trespassers out and the park’s inhabitants-millions of robots battling for survival and control of the factory-within. The winning robots get to spawn, their reproduction accomplished by programming the banks of 3-D printers inside. Step-by-step, the robots become smarter, faster-and deadlier. Robotic Park is run by the US Army, and its purpose is to evolve the ultimate soldier.

Robotic Park doesn’t exist yet, but it may someday. I suggested it as a thought experiment at a DARPA workshop a few years ago, and one of the military brass present said matter-of-factly, “That’s feasible.” His willingness might seem less startling if you consider that the army already runs a full-blown mockup of an Afghan village in the California desert, complete with villagers, for training its troops, and a few billion dollars would be a small price to pay for the ultimate soldier.

The first steps toward Robotic Park have already been taken. Inside Hod Lipson’s Creative Machines Lab at Cornell University, fantastically shaped robots are learning to crawl and fly, probably even as you read this. One looks like a slithering tower of rubber bricks, another like a helicopter with dragonfly wings, yet another like a shape-shifting Tinkertoy. These robots were not designed by any human engineer but created by evolution, the same process that gave rise to the diversity of life on Earth. Although the robots initially evolve inside a computer simulation, once they look proficient enough to make it in the real world, solid versions are automatically fabricated by 3-D printing. These are not yet ready to take over the world, but they’ve come a long way from the primordial soup of simulated parts they started with.

The algorithm that evolved these robots was invented by Charles Darwin in the nineteenth century. He didn’t think of it as an algorithm at the time, partly because a key subroutine was still missing. Once James Watson and Francis Crick provided it in 1953, the stage was set for the second coming of evolution: in silico instead of in vivo, and a billion times faster. Its prophet was a ruddy-faced, perpetually grinning midwesterner by the name of John Holland.

Darwin’s algorithm

Like many other early machine-learning researchers, Holland started out working on neural networks, but his interests took a different turn when, while a graduate student at the University of Michigan, he read Ronald Fisher’s classic treatise The Genetical Theory of Natural Selection. In it, Fisher, who was also the founder of modern statistics, formulated the first mathematical theory of evolution. Brilliant as it was, Holland felt that Fisher’s theory left out the essence of evolution. Fisher considered each gene in isolation, but an organism’s fitness is a complex function of all its genes. If genes are independent, the relative frequencies of their variants rapidly converge to the maximum fitness point and remain in equilibrium thereafter. But if genes interact, evolution-the search for maximum fitness-is vastly more complex. With one thousand genes, each with two variants, the genome has 2¹⁰⁰⁰ possible states, and no planet in the universe is remotely large or ancient enough to have tried them all out. Yet on Earth evolution has managed to come up with some remarkably fit organisms, and Darwin’s theory of natural selection explains how, at least qualitatively. Holland decided to turn it into an algorithm.

But first he had to graduate. Prudently, he picked a more conservative topic for his dissertation-Boolean circuits with cycles-and in 1959 he earned the world’s first PhD in computer science. His PhD advisor, Arthur Burks, nevertheless encouraged Holland’s interest in evolutionary computation and was instrumental in getting him a faculty job at Michigan and shielding him from senior colleagues who didn’t think that stuff was computer science. Burks himself was so open-minded because he had been a close collaborator of John von Neumann, who had proved the possibility of self-reproducing machines. Indeed, it had fallen to him to complete the work when von Neumann died of cancer in 1957. That von Neumann could prove that such machines are possible was quite remarkable, given the primitive state of genetics and computer science at the time. But his automaton just made exact copies of itself; evolving automata had to wait for Holland.

The key input to a genetic algorithm, as Holland’s creation came to be known, is a fitness function. Given a candidate program and some purpose it is meant to fill, the fitness function assigns the program a numeric score reflecting how well it fits the purpose. In natural selection, it’s questionable whether fitness can be interpreted this way: while the fitness of a wing for flight makes intuitive sense, evolution as a whole has no known purpose. Nevertheless, in machine learning having something like a fitness function is a no-brainer. If we need a program that can diagnose a patient, one that correctly diagnoses 60 percent of the patients in our database is better than one that only gets it right 55 percent of the time, and thus a possible fitness function is the fraction of correctly diagnosed cases.

In this regard, genetic algorithms are a lot like selective breeding. Darwin opened The Origin of Species with a discussion of it, as a stepping-stone to the more difficult concept of natural selection. All the domesticated plants and animals we take for granted today are the result of selecting and mating, generation after generation, the organisms that best served our purposes: the corn with the largest corncobs, the sweetest fruit trees, the shaggiest sheep, the hardiest horses. Genetic algorithms do the same, except they breed programs instead of living creatures, and a generation is a few seconds of computer time instead of a creature’s lifetime.

The fitness function encapsulates the human’s role in the process. But the more subtle part is nature’s. Starting with a population of not-very-fit individuals-possibly completely random ones-the genetic algorithm has to come up with variations that can then be selected according to fitness. How does nature do that? Darwin didn’t know. This is where the genetic part of the algorithm comes in. In the same way that DNA encodes an organism as a sequence of base pairs, we can encode a program as a string of bits. Instead of 0 and 1, the DNA alphabet has four characters-the four bases adenine, thymine, cytosine, and guanine-but that’s a superficial difference. Variations, whether in DNA sequences or bit strings, can be generated in several ways. The simplest approach is point mutation, flipping a random bit in the string or changing a single base in a stretch of DNA. But for Holland, the real power of genetic algorithms lay in something more complicated: sex.

Stripped down to its bare essentials (no giggles, please), sexual reproduction consists of swapping material between chromosomes from the mother and father, a process called crossing over. This produces two new chromosomes, one of which consists of the mother’s chromosome up to the crossover point and the father’s thereafter, and the other one is the opposite:

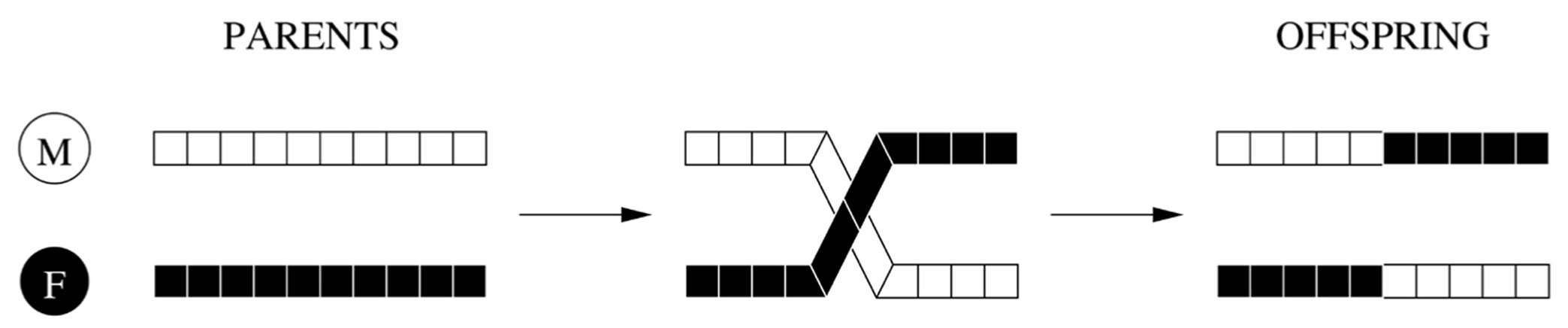
A genetic algorithm works by mimicking this process. In each generation, it mates the fittest individuals, producing two offspring from each pair of parents by crossing over their bit strings at a random point. After applying point mutations to the new strings, it lets them loose in its virtual world. Each one returns with a fitness score, and the process repeats. Each generation is fitter than the previous one, and the process terminates when the desired fitness is reached or time runs out.

For example, suppose we want to evolve a rule for filtering spam. If ten thousand different words appear in the training data, each candidate rule can be represented by a string of twenty thousand bits, two for each word. The first bit corresponding to the word free is one if e-mails containing free are allowed to match the rule, and zero if they’re not. The second bit is the opposite: one if e-mails not containing free are allowed to match, and zero if they’re not. So if both bits are one, e-mails are allowed to match the rule regardless of whether they contain free, and the rule effectively has no condition on that word. On the other hand, if both bits are zero, no e-mails match the rule, since one or the other bit always fails, and all e-mails get through the filter (yikes). Overall, an e-mail matches a rule only if its entire pattern of present and absent words is allowed by the rule. A rule’s fitness is, say, the percentage of e-mails it classifies correctly. Starting from a population of random strings, each representing a rule with random conditions, the genetic algorithm can now evolve better and better rules by repeatedly crossing over and mutating the fittest strings in each generation. For example, if the current population includes the rules If the e-mail contains the word free then it’s spam and If the e-mail contains the word easy then it’s spam, crossing them over will yield the probably fitter rule If the e-mail contains free and easy then it’s spam, provided the crossover point does not fall between the two bits corresponding to one of those words. It will also yield the rule All e-mail is spam, which results from dropping both conditions, but that rule is unlikely to have much progeny in the next generation.

Since our goal is to produce the best spam filter we can, as opposed to faithfully simulating real natural selection, we can cheat liberally by modifying the algorithm to fit our needs. One way in which genetic algorithms routinely cheat is by allowing immortality. (Too bad we can’t do that in real life.) That way, a highly fit individual doesn’t simply compete to reproduce within its own generation, but also with its children, and then its grandchildren, great-grandchildren, and so on, as long as it remains one of the fittest individuals in the population. In contrast, in the real world the best a highly fit individual can do is pass on half its genes to many children, each of which will probably be less fit because of the genes it inherited from its other parent. Immortality avoids this backsliding and with any luck, lets the algorithm reach the desired fitness sooner. Of course, since the fittest humans in history as measured by number of descendants are the likes of Genghis Khan-ancestor to one in two hundred men alive today-perhaps it’s not so bad that in real life immortality is verboten.

If we want to evolve a whole set of spam-filtering rules, not just one, we can represent a candidate set of n rules by a string of n ? 20,000 bits (20,000 for each rule, assuming ten thousand different words in the data, as before). Rules containing 00 for some word effectively disappear from the rule set, since they don’t match any e-mails, as we saw before. If an e-mail matches any rule in the set, it’s classified as spam; otherwise it’s legit. We can still let fitness be the percentage of correctly classified e-mails, but to combat overfitting, we’ll probably want to subtract from it a penalty proportional to the total number of active conditions in the rule set.

We can get even fancier by allowing rules for intermediate concepts to evolve, and then chaining these rules at performance time. For example, we could evolve the rules If the e-mail contains the word loan then it’s a scam and If the e-mail is a scam then it’s spam. Since a rule’s consequent is no longer always spam, this requires introducing additional bits in rule strings to represent their consequents. Of course, the computer doesn’t literally use the word scam; it just comes up with some arbitrary bit string to represent the concept, but that’s good enough for our purposes. Sets of rules like this, which Holland called classifier systems, are one of the workhorses of the machine-learning tribe he founded: the evolutionaries. Like multilayer perceptrons, classifier systems face the credit-assignment problem-what is the fitness of rules for intermediate concepts?-and Holland devised the so-called bucket brigade algorithm to solve it. Nevertheless, classifier systems are much less widely used than multilayer perceptrons.

Compared to the simple model in Fisher’s book, genetic algorithms are quite a leap forward. Darwin lamented his lack of mathematical ability, but if he had lived a century later he probably would have yearned for programming prowess instead. Indeed, capturing natural selection by a set of equations is extremely difficult, but expressing it as an algorithm is another matter, and can shed light on many otherwise vexing questions. Why do species appear suddenly in the fossil record? Where’s the evidence that they evolved gradually from earlier species? In 1972, Niles Eldredge and Stephen Jay Gould proposed that evolution consists of a series of “punctuated equilibria,” alternating long periods of stasis with short bursts of rapid change, like the Cambrian explosion. This sparked a heated debate, with critics of the theory nicknaming it “evolution by jerks” and Eldredge and Gould retorting that gradualism is “evolution by creeps.” Experience with genetic algorithms lends support to the jerks. If you run a genetic algorithm for one hundred thousand generations and observe the population at one-thousand-generation intervals, the graph of fitness against time will probably look like an uneven staircase, with sudden improvements followed by flat periods that tend to become longer over time. It’s also not hard to see why. Once the algorithm reaches a local maximum of fitness-a peak in the fitness landscape-it will stay there for a long time until a lucky mutation or crossover lands an individual on the slope to a higher peak, at which point that individual will multiply and climb up the slope with each passing generation. And the higher the current peak, the longer before that happens. Of course, natural evolution is more complicated than this: for one, the environment may change, either physically or because other organisms have themselves evolved, and an organism that was on a fitness peak may suddenly find itself under pressure to evolve again. So, while helpful, current genetic algorithms are far from the end of the story.

The exploration-exploitation dilemma

Notice how much genetic algorithms differ from multilayer perceptrons. Backprop entertains a single hypothesis at any given time, and the hypothesis changes gradually until it settles into a local optimum. Genetic algorithms consider an entire population of hypotheses at each step, and these can make big jumps from one generation to the next, thanks to crossover. Backprop proceeds deterministically after setting the initial weights to small random values. Genetic algorithms, in contrast, are full of random choices: which hypotheses to keep alive and cross over (with fitter hypotheses being more likely candidates), where to cross two strings, which bits to mutate. Backprop learns weights for a predefined network architecture; denser networks are more flexible but also harder to learn. Genetic algorithms make no a priori assumptions about the structures they will learn, other than their general form.

Because of all this, genetic algorithms are much less likely than backprop to get stuck in a local optimum and in principle better able to come up with something truly new. But they are also much more difficult to analyze. How do we know a genetic algorithm will get somewhere meaningful instead of randomly walking around like the proverbial drunkard? The key is to think in terms of building blocks. Every subset of a string’s bits potentially encodes a useful building block, and when we cross over two strings, those building blocks come together into a larger one, which in turn becomes grist for the mill. Holland likes to use police sketches to illustrate the power of building blocks. In the days before computers, a police artist could quickly put together a portrait of a suspect from eyewitness interviews by selecting a mouth from a set of paper strips depicting typical mouth shapes and doing the same for the eyes, nose, chin, and so on. With only ten building blocks and ten options for each, this system would allow for ten billion different faces, more than there are people on Earth.

In machine learning, as elsewhere in computer science, there’s nothing better than getting such a combinatorial explosion to work for you instead of against you. What’s clever about genetic algorithms is that each string implicitly contains an exponential number of building blocks, known as schemas, and so the search is a lot more efficient than it seems. This is because every subset of the string’s bits is a schema, representing some potentially fit combination of properties, and a string has an exponential number of subsets. We can represent a schema by replacing the bits in the string that aren’t part of it with *. For example, the string 110 contains the schemas ***, **0, *1*, 1**, *10, 11*, 1*0, and 110. We get a different schema for every different choice of bits to include; since we have two choices for each bit (include/don’t include), we have 2n schemas. Conversely, a particular schema may be represented in many different strings in a population, and is implicitly evaluated every time they are. Suppose that a hypothesis’s probability of surviving into the next generation is proportional to its fitness. Holland showed that, in this case, the fitter a schema’s representatives in one generation are compared to the average, the more of them we can expect to see in the next generation. So, while the genetic algorithm explicitly manipulates strings, it implicitly searches the much larger space of schemas. Over time, fitter schemas come to dominate the population, and so unlike the drunkard, the genetic algorithm finds its way home.

One of the most important problems in machine learning-and life-is the exploration-exploitation dilemma. If you’ve found something that works, should you just keep doing it? Or is it better to try new things, knowing it could be a waste of time but also might lead to a better solution? Would you rather be a cowboy or a farmer? Start a company or run an existing one? Go steady or play the field? A midlife crisis is the yearning to explore after many years spent exploiting. On an impulse, you fly to Vegas, ready to gamble away your life’s savings on the chance of becoming a millionaire. You enter the first casino and face a row of slot machines. The one to play is the one that gives you the best payoff on average, but you don’t know which that is. You have to try each one enough times to figure it out. But if you do this for too long, you waste your money on losing machines. Conversely, if you jump the gun and pick a machine that looked good by chance on the first few turns but is in fact not the best one, you waste your money playing it for the rest of the night. That’s the exploration-exploitation dilemma. Each time you play, you have to choose between repeating the best move you’ve found so far, which gives you the best payoff, or trying other moves, which gather information that may lead to even better payoffs. With two slot machines, Holland showed that the optimal strategy is to flip a biased coin each time, where the coin becomes exponentially more biased as you go along. (Don’t sue me if it doesn’t work for you, though. Remember the house always wins in the end.) The better a slot machine looks, the more you should play it, but never completely give up on the other one, in case it turns out to be the best one after all.

A genetic algorithm is like the ringleader of a group of gamblers, playing slot machines in every casino in town at the same time. Two schemas compete with each other if they include the same bits and differ in at least one of them, like *10 and *11, and n competing schemas are like n slot machines. Every set of competing schemas is a casino, and the genetic algorithm simultaneously figures out the winning machine in every casino, following the optimal strategy of playing the better-seeming machines with exponentially increasing frequency. Pretty smart.

In The Hitchhiker’s Guide to the Galaxy, an alien race builds a massive supercomputer to answer the ultimate question, and after a long time the computer spits out “42.” But the computer also points out that the aliens don’t know what the question is, so they build an even bigger computer to figure that out. This computer-otherwise known as planet Earth-is unfortunately destroyed to make way for a space freeway minutes before finishing its multimillion-year computation. We can only guess at the question now, but perhaps it was: Which slot machine should you play?

Survival of the fittest programs

For the first few decades, the genetic algorithms community consisted mainly of John Holland, his students, and their students. Circa 1983, the biggest problem genetic algorithms had been able to solve was learning to control gas pipeline systems. But then, at around the same time neural networks were making their comeback, interest in evolutionary computation took off. The first international conference on genetic algorithms was held in Pittsburgh in 1985, and a Cambrian explosion of genetic algorithm variants was under way. Some of these tried to model evolution more closely-the basic genetic algorithm was only a very crude approximation, after all-and others radiated in very different directions, crossing over evolutionary ideas with computer science concepts that would have bemused Darwin.

One of Holland’s more remarkable students was John Koza. In 1987, while flying back to California from a conference in Italy, he had a lightbulb moment. Instead of evolving comparatively simple things like If… then… rules and gas pipeline controllers, why not evolve full-blown computer programs? And if that’s the goal, why stick with bit strings as the representation? A program is really a tree of subroutine calls, so better to directly cross over those subtrees than to shoehorn them into bit strings and run the risk of destroying perfectly good subroutines when you cross them over at a random point.

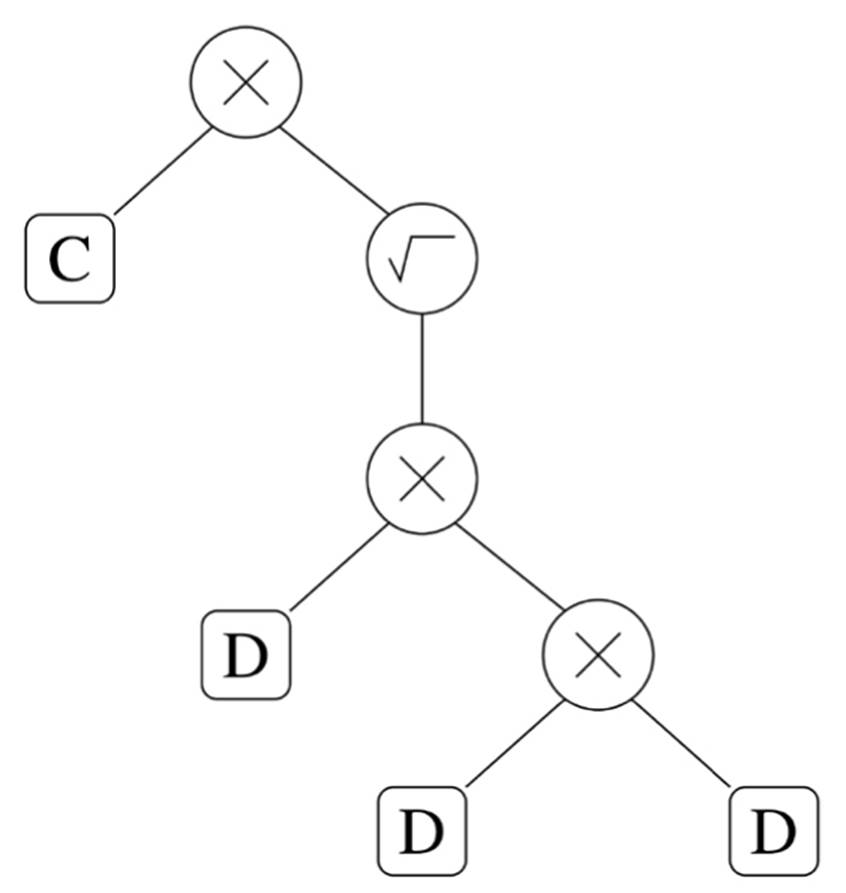
For example, suppose you want to evolve a program to compute the duration of a planet’s year, T, from its average distance to the sun, D. According to Kepler’s third law, T is the square root of D cubed, times a constant C that depends on the units you use for time and distance. A genetic algorithm should be able to discover this by looking at Tycho Brahe’s data on planetary motions like Kepler did. In Koza’s approach, D and C are the leaves of a program tree, and the operations that combine them, like multiplication and taking the square root, are the internal nodes. The following program tree correctly computes T:

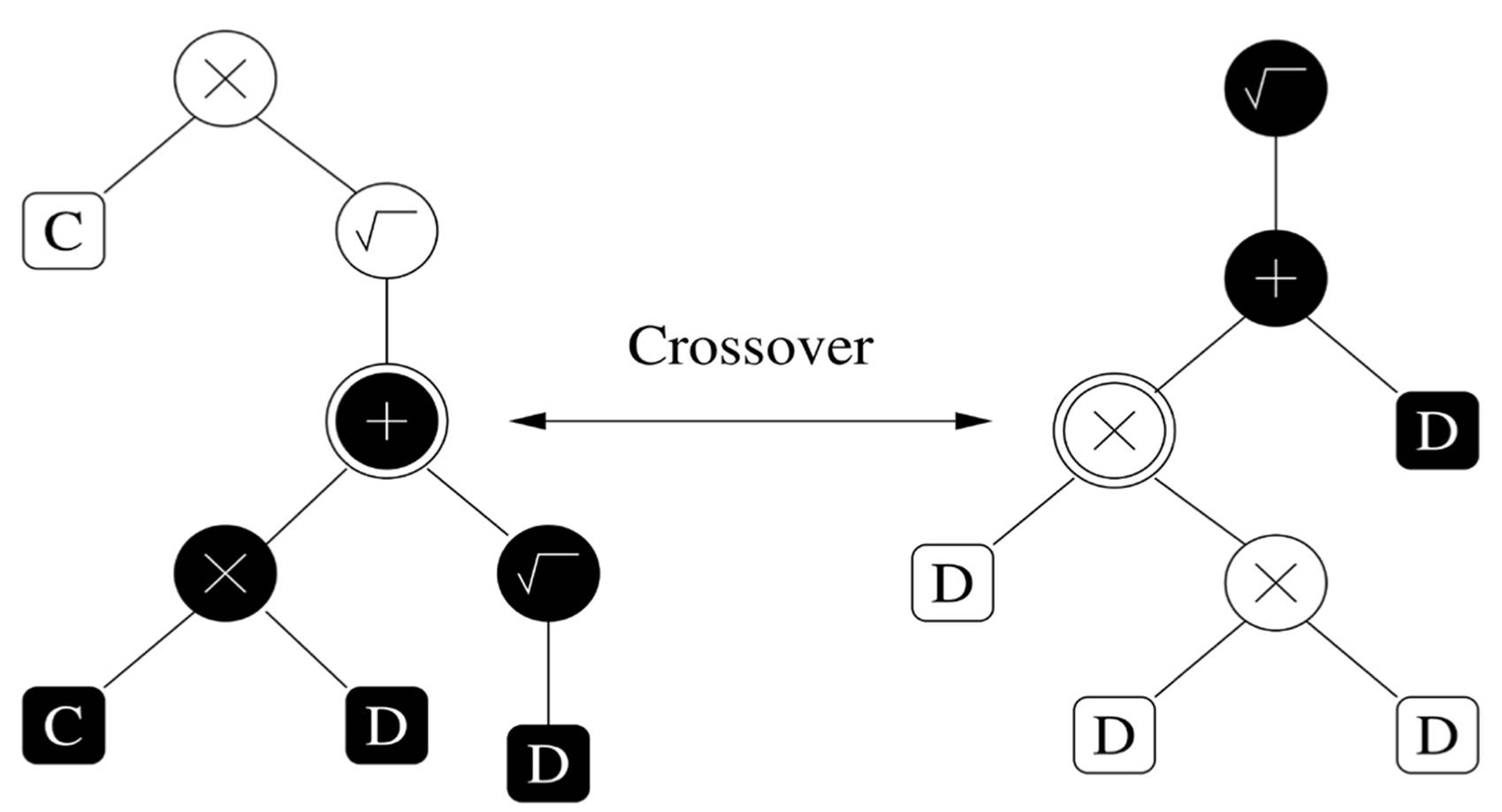
In genetic programming, as Koza called his method, we cross over two program trees by randomly swapping two of their subtrees. For example, crossing over these two trees at the highlighted nodes yields the correct program for computing T as one of the children:

We can measure a program’s fitness (or lack thereof) by the distance between its output and the correct one on the training data. For example, if the program says an Earth year is three hundred days, that would subtract sixty-five points from its fitness. Starting with a population of random program trees, genetic programming uses crossover, mutation, and survival to gradually evolve better programs until it’s satisfied.

Of course, computing the length of a planet’s year is a very simple problem, involving only multiplication and square roots. In general, program trees can include the full range of programming constructs, such as If… then… statements, loops, and recursion. A more illustrative example of what genetic programming can do is figuring out the sequence of actions a robot needs to perform to achieve some goal. Suppose I ask my officebot to bring me a stapler from the closet down the hall. The robot has a large set of behaviors available to it, such as moving down a hallway, opening a door, picking up an object, and so on. Each of these can in turn be composed of various sub-behaviors: move the robot’s hand toward the object, or grasp it at various possible points, for example. Each behavior may be executed or not depending on the results of previous behaviors, may need to be repeated some number of times, and so on. The challenge is to assemble the right structure of behaviors and sub-behaviors, together with the parameters for each, such as how far to move the hand. Starting with the robot’s “atomic” behaviors and their allowed combinations, genetic programming can assemble a complex behavior that accomplishes the desired goal. A number of researchers have evolved strategies for robot soccer players in this way.

One consequence of crossing over program trees instead of bit strings is that the resulting programs can have any size, making the learning more flexible. The overall tendency is for bloat, however, with larger and larger trees growing as evolution goes on longer (also known as “survival of the fattest”). Evolutionaries can take comfort from the fact that human-written programs are no different (Microsoft Windows: forty-five million lines of code and counting), and that human-made code doesn’t allow a solution as simple as adding a complexity penalty to the fitness function.

Genetic programming’s first success, in 1995, was in designing electronic circuits. Starting with a pile of electronic components such as transistors, resistors, and capacitors, Koza’s system reinvented a previously patented design for a low-pass filter, a circuit that can be used for things like enhancing the bass on a dance-music track. Since then he’s made a sport of reinventing patented devices, turning them out by the dozen. The next milestone came in 2005, when the US Patent and Trademark Office awarded a patent to a genetically designed factory optimization system. If the Turing test had been to fool a patent examiner instead of a conversationalist, then January 25, 2005, would have been a date for the history books.

Koza’s confidence stands out even in a field not known for its shrinking violets. He sees genetic programming as an invention machine, a silicon Edison for the twenty-first century. He and other evolutionaries believe it can learn any program, making it their entry in the Master Algorithm sweepstakes. In 2004, they instituted the annual Humie Awards to recognize “human-competitive” genetic creations; thirty-nine have been awarded to date.

What is sex for?

Despite their successes, and the insights they’ve provided on issues like gradualism versus punctuated equilibria, genetic algorithms have left one great mystery unsolved: the role of sex in evolution. Evolutionaries set great store by crossover, but members of the other tribes think it’s not worth the trouble. None of Holland’s theoretical results show that crossover actually helps; mutation suffices to exponentially increase the frequency of the fittest schemas in the population over time. And the “building blocks” intuition is appealing but quickly runs into trouble, even when genetic programming is used. As larger blocks evolve, crossover also becomes increasingly likely to break them up. Also, once a highly fit individual appears, its descendants tend to quickly take over the population, crowding out potentially better schemas that were trapped in overall less fit individuals. This effectively reduces the search to variations of the fitness champ. Researchers have come up with a number of schemes for preserving diversity in the population, but the results so far are inconclusive. Engineers certainly use building blocks extensively, but combining them involves, well, a lot of engineering; it’s not just a matter of throwing them together any old way, and it’s not clear crossover can do the trick.

Eliminating sex would leave evolutionaries with only mutation to power their engine. If the size of the population is substantially larger than the number of genes, chances are that every point mutation is represented in it, and the search becomes a type of hill climbing: try all possible one-step variations, pick the best one, and repeat. (Or pick several of the best variations, in which case it’s called beam search.) Symbolists, in particular, use this all the time to learn sets of rules, although they don’t think of it as a form of evolution. To avoid getting trapped in local maxima, hill climbing can be enhanced with randomness (make a downhill move with some probability) and random restarts (after a while, jump to a random state and continue from there). Doing this is enough to find good solutions to problems; whether the benefit of adding crossover to it justifies the extra computational cost remains an open question.

No one is sure why sex is pervasive in nature, either. Several theories have been proposed, but none is widely accepted. The leader of the pack is the Red Queen hypothesis, popularized by Matt Ridley in the eponymous book. As the Red Queen said to Alice in Through the Looking Glass, “It takes all the running you can do, to keep in the same place.” In this view, organisms are in a perpetual arms race with parasites, and sex helps keep the population varied, so that no single germ can infect all of it. If this is the answer, then sex is irrelevant to machine learning, at least until learned programs have to vie with computer viruses for processor time and memory. (Intriguingly, Danny Hillis claims that deliberately introducing coevolving parasites into a genetic algorithm can help it escape local maxima by gradually ratcheting up the difficulty, but no one has followed up on this yet.) Christos Papadimitriou and colleagues have shown that sex optimizes not fitness but what they call mixability: a gene’s ability to do well on average when combined with other genes. This can be useful when the fitness function is either not known or not constant, as in natural selection, but in machine learning and optimization, hill climbing tends to do better.

The problems for genetic programming do not end there. Indeed, even its successes might not be as genetic as evolutionaries would like. Take circuit design, which was genetic programming’s emblematic success. As a rule, even relatively simple designs require an enormous amount of search, and it’s not clear how much the results owe to brute force rather than genetic smarts. To address the growing chorus of critics, Koza included in his 1992 book Genetic Programming experiments showing that genetic programming beat randomly generating candidates on Boolean circuit synthesis problems, but the margin of victory was small. Then, at the 1995 International Conference on Machine Learning (ICML) in Lake Tahoe, California, Kevin Lang published a paper showing that hill climbing beat genetic programming on the same problems, often by a large margin. Koza and other evolutionaries had repeatedly tried to publish papers in ICML, a leading venue in the field, but to their increasing frustration they kept being rejected due to insufficient empirical validation. Already frustrated with his papers being rejected, seeing Lang’s paper made Koza blow his top. On short order, he produced a twenty-three-page paper in two-column ICML format refuting Lang’s conclusions and accusing the ICML reviewers of scientific misconduct. He then placed a copy on every seat in the conference auditorium. Depending on your point of view, either Lang’s paper or Koza’s response was the last straw; regardless, the Tahoe incident marked the final divorce between the evolutionaries and the rest of the machine-learning community, with the evolutionaries moving out of the house. Genetic programmers started their own conference, which merged with the genetic algorithms conference to form GECCO, the Genetic and Evolutionary Computing Conference. For its part, the machine-learning mainstream largely forgot them. A sad d?nouement, but not the first time in history that sex is to blame for a breakup.

Sex may not have succeeded in machine learning, but as a consolation, it has played a prominent role in the evolution of technology in other ways. Pornography was the unacknowledged “killer app” of the World Wide Web, not to mention the printing press, photography, and video before it. The vibrator was the first handheld electrical device, predating the cell phone by a century. Scooters took off in postwar Europe, particularly Italy, because they let young couples get away from their families. Facilitating dating was surely one of the “killer apps” of fire when Homo erectus discovered it a million years ago; and equally surely, a key driver of increasing realism in humanlike robots will be the sexbot industry. Sex just seems to be the end, rather than the means, of technological evolution.

Nurturing nature

Evolutionaries and connectionists have something important in common: they both design learning algorithms inspired by nature. But then they part ways. Evolutionaries focus on learning structure; to them, fine-tuning an evolved structure by optimizing parameters is of secondary importance. In contrast, connectionists prefer to take a simple, hand-coded structure with lots of connections and let weight learning do all the work. This is machine learning’s version of the nature versus nurture controversy, and there are good arguments on both sides.

On the one hand, evolution has produced many amazing things, none more amazing than you. With or without crossover, evolving structure is an essential part of the Master Algorithm. The brain can learn anything, but it can’t evolve a brain. If we thoroughly understood its architecture, we could just implement it in hardware, but we’re very far from that; getting an assist from computer-simulated evolution is a no-brainer. What’s more, we also want to evolve the brains of robots, systems with arbitrary sensors, and super-AIs. There’s no reason to stick with the design of the human brain if there are better ones for those tasks. On the other hand, evolution is excruciatingly slow. The entire life of an organism yields only one piece of information about its genome: its fitness, reflected in the organism’s number of offspring. That’s a colossal waste of information, which neural learning avoids by acquiring the information at the point of use (so to speak). As connectionists like Geoff Hinton like to point out, there’s no advantage to carrying around in the genome information that we can readily acquire from the senses. When a newborn opens his eyes, the visual world comes flooding in; the brain just has to organize it. What does need to be specified in the genome, however, is the architecture of the machine that does the organizing.

As in the nature versus nurture debate, neither side has the whole answer; the key is figuring out how to combine the two. The Master Algorithm is neither genetic programming nor backprop, but it has to include the key elements of both: structure learning and weight learning. In the conventional view, nature does its part first-evolving a brain-and then nurture takes it from there, filling the brain with information. We can easily reproduce this in learning algorithms. First, learn the structure of the network, using (for example) hill climbing to decide which neurons connect to which: try adding each possible new connection to the network, keep the one that most improves performance, and repeat. Then learn the connection weights using backprop, and your brand-new brain is ready to use.

But now there’s an important subtlety, in both natural and artificial evolution. We need to learn weights for every candidate structure along the way, not just the final one, in order to see how well it does in the struggle for life (in the natural case) or on the training data (in the artificial case). The structure we want to select at each step is the one that does best after learning weights, not before. So in reality, nature does not come before nurture; rather, they alternate, with each round of “nurture” learning setting the stage for the next round of “nature” learning and vice versa. Nature evolves for the nurture it gets. The evolutionary growth of the cortex’s associative areas builds on neural learning in the sensory areas, without which it would be useless. Goslings follow their mother around (evolved behavior) but that requires recognizing her (learned ability). If you’re the first thing they see when they hatch, they’ll follow you instead, as Konrad Lorenz memorably showed. The newborn brain already encodes features of the environment but not explicitly; rather, evolution optimized it to extract those features from the expected input. Likewise, in an algorithm that iteratively learns both structure and weights, each new structure is implicitly a function of the weights learned in previous rounds.

Of all the possible genomes, very few correspond to viable organisms. The typical fitness landscape thus consists of vast flatlands with occasional sharp peaks, making evolution very hard. If you start out blindfolded in Kansas, you have no idea which way the Rockies lie, and you’ll wander around for a long time before you bump into their foothills and start climbing. But if you combine evolution with neural learning, something interesting happens. If you’re on flat ground, but not too far from the foothills, neural learning can get you there, and the closer you are to the foothills, the more likely it will. It’s like being able to scan the horizon: it won’t help you in Wichita, but in Denver you’ll see the Rockies in the distance and head that way. Denver now looks a lot fitter than it did when you were blindfolded. The net effect is to widen the fitness peaks, making it possible for you to find your way to them from previously very tough places, like point A in this graph:

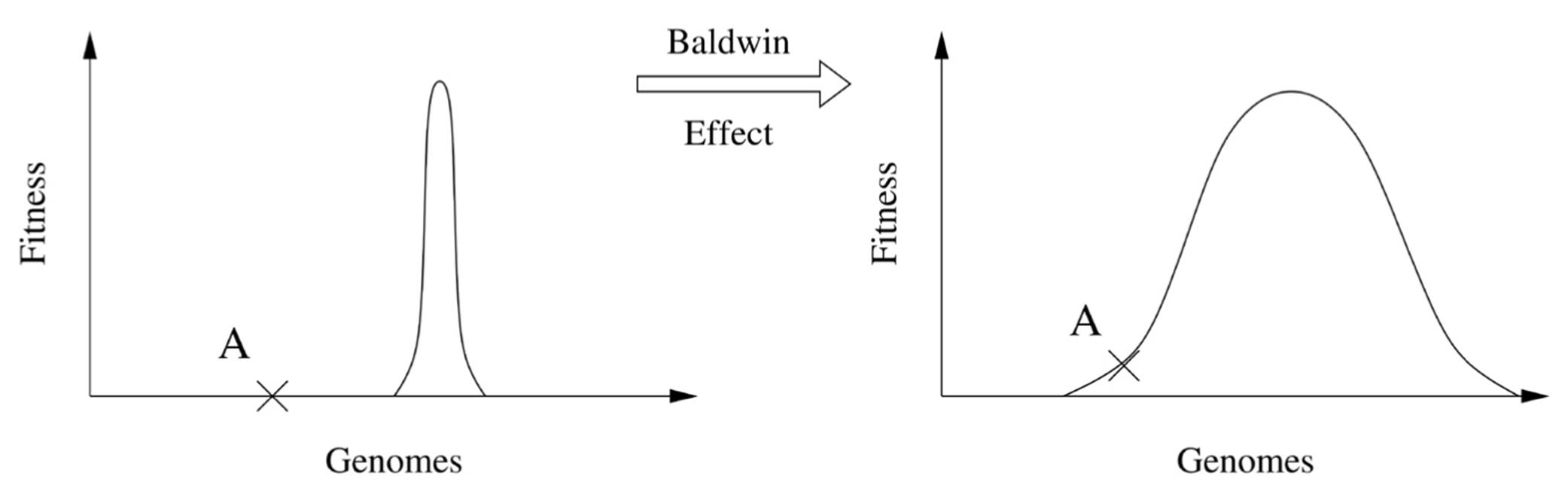
In biology, this is called the Baldwin effect, after J. M. Baldwin, who proposed it in 1896. In Baldwinian evolution, behaviors that are first learned later become genetically hardwired. If dog-like mammals can learn to swim, they have a better chance to evolve into seals-as they did-than if they drown. Thus individual learning can influence evolution without recourse to Lamarckism. Geoff Hinton and Steven Nowlan demonstrated the Baldwin effect in machine learning by using genetic algorithms to evolve neural network structure and observing that fitness increased over time only when individual learning was allowed.

He who learns fastest wins

Evolution searches for good structures, and neural learning fills them in: this combination is the easiest of the steps we’ll take toward the Master Algorithm. This may come as a surprise to anyone familiar with the never-ending twists and turns of the nature versus nurture controversy, 2,500 years old and still going strong. Seeing life through the eyes of a computer clarifies a lot of things, however. “Nature” for a computer is the program it runs, and “nurture” is the data it gets. The question of which one is more important is clearly absurd; there’s no output without both program and data, and it’s not like the output is, say, 60 percent caused by the program and 40 percent by the data. That’s the kind of linear thinking that a familiarity with machine learning immunizes you against.

On the other hand, you may be wondering why we’re not done at this point. Surely if we’ve combined nature’s two master algorithms, evolution and the brain, that’s all we could ask for. Unfortunately, what we have so far is only a very crude cartoon of how nature learns, good enough for a lot of applications but still a pale shadow of the real thing. For example, the development of the embryo is a crucial part of life, but there’s no analog of it in machine learning: the “organism” is a very straightforward function of the genome, and we may be missing something important there. But another reason is that we wouldn’t be satisfied even if we had completely figured out how nature learns. For one thing, it’s too slow. Evolution takes billions of years to learn, and the brain takes a lifetime. Culture is better: I can distill a lifetime of learning into a book, and you can read it in a few hours. But learning algorithms should be able to learn in minutes or seconds. He who learns fastest wins, whether it’s the Baldwin effect speeding up evolution, verbal communication speeding up human learning, or computers discovering patterns at the speed of light. Machine learning is the latest chapter in the arms race of life on Earth, and swifter hardware is only half the equation. The other half is smarter software.

Most of all, the goal of machine learning is to find the best possible learning algorithm, by any means available, and evolution and the brain are unlikely to provide it. The products of evolution have many obvious faults. For example, the mammalian optic nerve attaches to the front of the retina instead of the back, causing an unnecessary-and egregious-blind spot right next to the fovea, the area of sharpest vision.

The molecular biology of living cells is such a mess that molecular biologists often quip that only people who don’t know any of it could believe in intelligent design. The architecture of the brain may well have similar faults-the brain has many constraints that computers don’t, like very limited short-term memory-and there’s no reason to stay within them. Moreover, we know of many situations where humans seem to consistently do the wrong thing, as Daniel Kahneman illustrates at length in his book Thinking, Fast and Slow.

In contrast to the connectionists and evolutionaries, symbolists and Bayesians do not believe in emulating nature. Rather, they want to figure out from first principles what learners should do-and that includes us humans. If we want to learn to diagnose cancer, for example, it’s not enough to say “this is how nature learns; let’s do the same.” There’s too much at stake. Errors cost lives. Doctors should diagnose in the most foolproof way they can, with methods similar to those mathematicians use to prove theorems, or as close to that as they can manage, given that it’s seldom possible to be that rigorous. They need to weigh the evidence to minimize the chances of a wrong diagnosis; or more precisely, so that the costlier an error is, the less likely they are to make it. (For example, failing to find a tumor that’s really there is potentially much worse than inferring one that isn’t.) They need to make optimal decisions, not just decisions that seem good.

This is an instance of a tension that runs throughout much of science and philosophy: the split between descriptive and normative theories, between “this is how it is” and “this is how it should be.” Symbolists and Bayesians like to point out, however, that figuring out how we should learn can also help us to understand how we do learn because the two are presumably not entirely unrelated-far from it. In particular, behaviors that are important for survival and have had a long time to evolve should not be far from optimal. We’re not very good at answering written questions about probabilities, but we are very good at instantly choosing hand and arm movements to hit a target. Many psychologists have used symbolist or Bayesian models to explain aspects of human behavior. Symbolists dominated the first few decades of cognitive psychology. In the 1980s and 1990s, connectionists held sway, but now Bayesians are on the rise.

For the hardest problems-the ones we really want to solve but haven’t been able to, like curing cancer-pure nature-inspired approaches are probably too uninformed to succeed, even given massive amounts of data. We can in principle learn a complete model of a cell’s metabolic networks by a combination of structure search, with or without crossover, and parameter learning via backpropagation, but there are too many bad local optima to get stuck in. We need to reason with larger chunks, assembling and reassembling them as needed and using inverse deduction to fill in the gaps. And we need our learning to be guided by the goal of optimally diagnosing cancer and finding the best drugs to cure it.

Optimal learning is the Bayesians’ central goal, and they are in no doubt that they’ve figured out how to reach it. This way, please…

Оглавление книги