Книга: The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World

CHAPTER SEVEN: You Are What You Resemble

CHAPTER SEVEN: You Are What You Resemble

Frank Abagnale Jr. is one of the most notorious con men in history. Abagnale, portrayed by Leonardo DiCaprio in Spielberg’s movie Catch Me If You Can, forged millions of dollars’ worth of checks, impersonated an attorney and a college instructor, and traveled the world as a fake Pan Am pilot-all before his twenty-first birthday. But perhaps his most jaw-dropping exploit was to successfully pose as a doctor for nearly a year in late-1960s Atlanta. Practicing medicine supposedly requires many years in med school, a license, a residency, and whatnot, but Abagnale managed to bypass all these niceties and never got called on it.

Imagine for a moment trying to pull off such a stunt. You sneak into an absent doctor’s office, and before long a patient comes in and tells you all his symptoms. Now you have to diagnose him, except you know nothing about medicine. All you have is a cabinet full of patient files: their symptoms, diagnoses, treatments undergone, and so on. What do you do? The easiest way out is to look in the files for the patient whose symptoms most closely resemble your current one’s and make the same diagnosis. If your bedside manner is as convincing as Abagnale’s, that might just do the trick. The same idea applies well beyond medicine. If you’re a young president faced with a world crisis, as Kennedy was when a US spy plane revealed Soviet nuclear missiles being deployed in Cuba, chances are there’s no script ready to follow. Instead, you look for historical analogs of the current situation and try to learn from them. The Joint Chiefs of Staff urged an attack on Cuba, but Kennedy, having just read The Guns of August, a best-selling account of the outbreak of World War I, was keenly aware of how easily that could escalate into all-out war. So he opted for a naval blockade instead, perhaps saving the world from nuclear war.

Analogy was the spark that ignited many of history’s greatest scientific advances. The theory of natural selection was born when Darwin, on reading Malthus’s Essay on Population, was struck by the parallels between the struggle for survival in the economy and in nature. Bohr’s model of the atom arose from seeing it as a miniature solar system, with electrons as the planets and the nucleus as the sun. Kekul? discovered the ring shape of the benzene molecule after daydreaming of a snake eating its own tail.

Analogical reasoning has a distinguished intellectual pedigree. Aristotle expressed it in his law of similarity: if two things are similar, the thought of one will tend to trigger the thought of the other. Empiricists like Locke and Hume followed suit. Truth, said Nietzche, is a mobile army of metaphors. Kant was also a fan. William James believed that “this sense of sameness is the very keel and backbone of our thinking.” Some contemporary psychologists even argue that human cognition in its entirety is a fabric of analogies. We rely on it to find our way around a new town and to understand expressions like “see the light” and “stand tall.” Teenagers who insert “like” into every sentence they say would probably, like, agree that analogy is important, dude.

Given all this, it’s not surprising that analogy plays a prominent role in machine learning. It got off to a slow start, though, and was initially overshadowed by neural networks. Its first algorithmic incarnation appeared in an obscure technical report written in 1951 by two Berkeley statisticians, Evelyn Fix and Joe Hodges, and was not published in a mainstream journal until decades later. But in the meantime, other papers on Fix and Hodges’s algorithm started to appear and then to multiply until it was one of the most researched in all of computer science. The nearest-neighbor algorithm, as it’s called, is the first stop on our tour of analogy-based learning. The second is support vector machines, an idea that took machine learning by storm around the turn of the millennium and was only recently overshadowed by deep learning. The third and last is full-blown analogical reasoning, which has been a staple of psychology and AI for several decades, and a background theme in machine learning for nearly as long.

The analogizers are the least cohesive of the five tribes. Unlike the others, which have a strong identity and common ideals, the analogizers are more of a loose collection of researchers, united only by their reliance on similarity judgments as the basis for learning. Some, like the support vector machine folks, might even object to being brought under such an umbrella. But it’s raining deep models outside, and I think they would benefit greatly from making common cause. Similarity is one of the central ideas in machine learning, and the analogizers in all their guises are its keepers. Perhaps in a future decade, machine learning will be dominated by deep analogy, combining in one algorithm the efficiency of nearest-neighbor, the mathematical sophistication of support vector machines, and the power and flexibility of analogical reasoning. (There, I just gave away one of my secret research projects.)

Match me if you can

Nearest-neighbor is the simplest and fastest learning algorithm ever invented. In fact, you could even say it’s the fastest algorithm of any kind that could ever be invented. It consists of doing exactly nothing, and therefore takes zero time to run. Can’t beat that. If you want to learn to recognize faces and have a vast database of images labeled face/not face, just let it sit there. Don’t worry, be happy. Without knowing it, those images already implicitly form a model of what a face is. Suppose you’re Facebook and you want to automatically identify faces in photos people upload as a prelude to tagging them with their friends’ names. It’s nice to not have to do anything, given that Facebook users upload upward of three hundred million photos per day. Applying any of the learners we’ve seen so far to them, with the possible exception of Na?ve Bayes, would take a truckload of computers. And Na?ve Bayes is not smart enough to recognize faces.

Of course, there’s a price to pay, and the price comes at test time. Jane User has just uploaded a new picture. Is it a face? Nearest-neighbor’s answer is: find the picture most similar to it in Facebook’s entire database of labeled photos-its “nearest neighbor”-and if that picture contains a face, so does this one. Simple enough, but now you have to scan through potentially billions of photos in (ideally) a fraction of a second. Like a lazy student who doesn’t bother to study for the test, nearest-neighbor is caught unprepared and has to scramble. But unlike real life, where your mother taught you to never leave until tomorrow what you can do today, in machine learning procrastination can really pay off. In fact, the entire genre of learning that nearest-neighbor is part of is sometimes called “lazy learning,” and in this context there’s nothing pejorative about the term.

The reason lazy learners are a lot smarter than they seem is that their models, although implicit, can in fact be extremely sophisticated. Consider the extreme case where we have only one example of each class. For instance, we’d like to guess where the border between two countries is, but all we know is their capitals’ locations. Most learners would be stumped, but nearest-neighbor happily guesses that the border is a straight line lying halfway between the two cities:

The points on the line are at the same distance from the two capitals; points to the left of the line are closer to Positiville, so nearest-neighbor assumes they’re part of Posistan and vice versa. Of course, it would be a lucky day if that was the exact border, but as an approximation it’s probably a lot better than nothing. It’s when we know a lot of towns on both sides of the border, though, that things get really interesting:

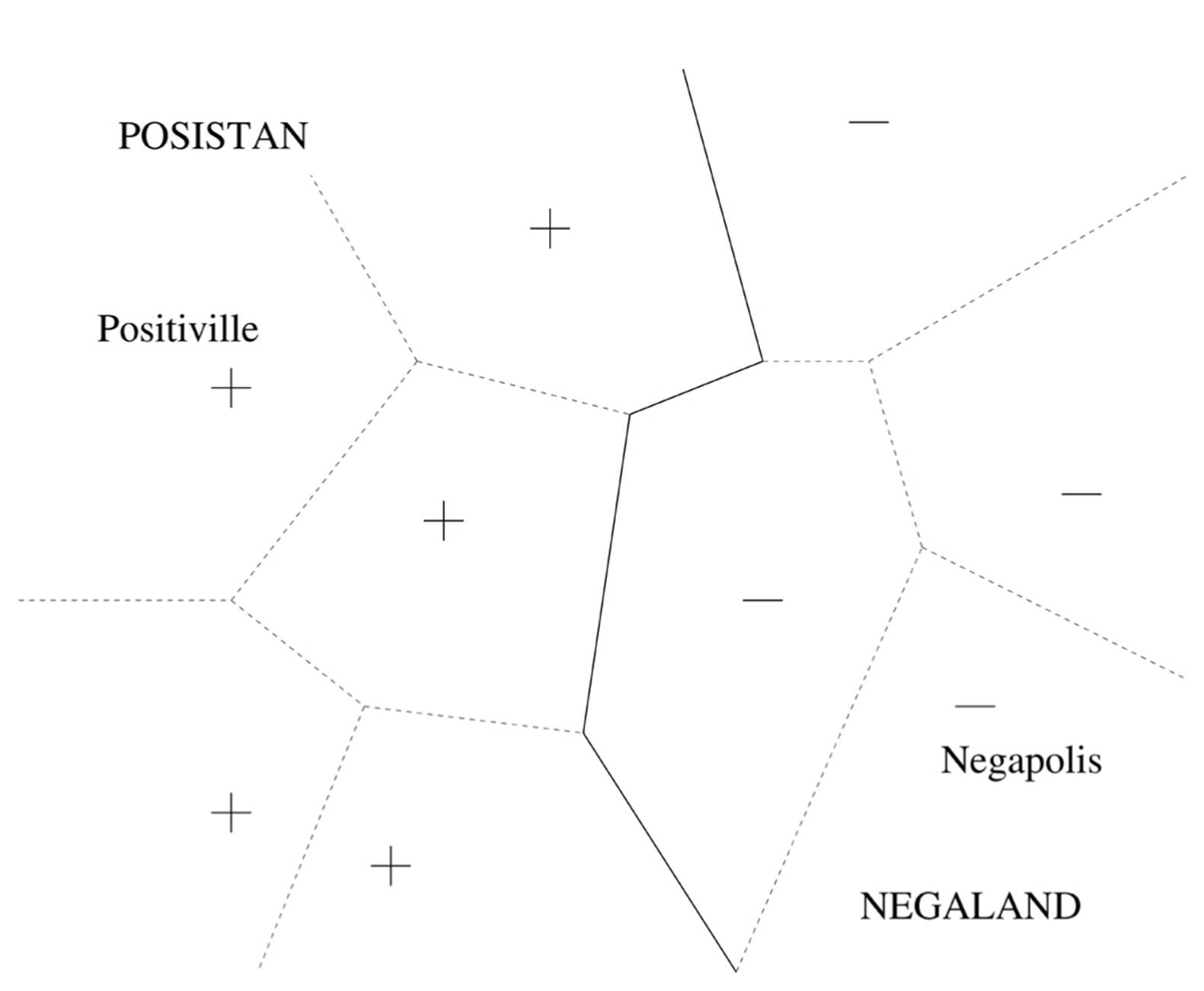
Nearest-neighbor is able to implicitly form a very intricate border, even though all it’s doing is remembering where the towns are and assigning points to countries accordingly! We can think of the “metro area” of a town as all the points that are closer to it than to any other town; the boundaries between metro areas are shown as dashed lines in the diagram. Now Posistan is just the union of the metro areas of all its cities, as is Negaland. In contrast, a decision tree (for example) would only be able to form borders running alternately north-south and east-west, probably a much worse approximation to the real border. Thus, even though decision tree learners are “eager,” trying hard at learning time to figure out where the border lies, “lazy” nearest-neighbor actually wins out.

The reason lazy learning wins is that forming a global model, such as a decision tree, is much harder than just figuring out where specific query points lie, one at a time. Imagine trying to define what a face is with a decision tree. You could say it has two eyes, a nose, and a mouth, but what is an eye and how do you find it in an image? What if the person’s eyes are closed? Reliably defining a face all the way down to individual pixels is extremely difficult, particularly given all the different expressions, poses, contexts, and lighting conditions a face could appear in. Instead, nearest-neighbor takes a shortcut: if the image in its database most similar to the one Jane just uploaded is of a face, then so is Jane’s. For this to work, the database needs to contain an image that’s similar enough to the new one-for example, a face with similar pose, lighting, and so on-so the bigger the database, the better. For a simple two-dimensional problem like guessing the border between two countries, a tiny database suffices. For a very hard problem like identifying faces, where the color of each pixel is a dimension of variation, we need a huge database. But these days we have them. Learning from them may be too costly for an eager learner, which explicitly draws the border between faces and nonfaces. For nearest-neighbor, however, the border is implicit in the locations of the data points and the distance measure, and the only cost is at query time.

The same idea of forming a local model rather than a global one applies beyond classification. Scientists routinely use linear regression to predict continuous variables, but most phenomena are not linear. Luckily, they’re locally linear because smooth curves are locally well approximated by straight lines. So if instead of trying to fit a straight line to all the data, you just fit it to the points near the query point, you now have a very powerful nonlinear regression algorithm. Laziness pays. If Kennedy had needed a complete theory of international relations to decide what to do about the Soviet missiles in Cuba, he would have been in trouble. Instead, he saw an analogy between that crisis and the outbreak of World War I, and that analogy guided him to the right decisions.

Nearest-neighbor can save lives, as Steven Johnson recounted in The Ghost Map. In 1854, London was struck by a cholera outbreak, which killed as many as one in eight people in parts of the city. The then-prevailing theory that cholera was caused by “bad air” did nothing to prevent its spread. But John Snow, a physician who was skeptical of the theory, had a better idea. He marked on a map of London the locations of all the known cases of cholera and divided the map into the regions closest to each public water pump. Eureka: nearly all deaths were in the “metro area” of one particular pump, located on Broad Street in the Soho district. Inferring that the water in that well was contaminated, Snow convinced the locals to disable the pump, and the epidemic died out. This episode gave birth to the science of epidemiology, but it’s also the first success of the nearest-neighbor algorithm-almost a century before its official invention.

With nearest-neighbor, each data point is its own little classifier, predicting the class for all the query examples it wins. Nearest-neighbor is like an army of ants, in which each soldier by itself does little, but together they can move mountains. If an ant’s load is too heavy, it can share it with its neighbors. In the same spirit, in the k-nearest-neighbor algorithm, a test example is classified by finding its k nearest neighbors and letting them vote. If the nearest image to the new upload is a face but the next two nearest ones aren’t, three-nearest-neighbor decides that the new upload is not a face after all. Nearest-neighbor is prone to overfitting: if we have the wrong class for a data point, it spreads to its entire metro area. K-nearest-neighbor is more robust because it only goes wrong if a majority of the k nearest neighbors is noisy. The price, of course, is that its vision is blurrier: fine details of the frontier get washed away by the voting. When k goes up, variance decreases, but bias increases.

Using the k nearest neighbors instead of one is not the end of the story. Intuitively, the examples closest to the test example should count for more. This leads us to the weighted k-nearest-neighbor algorithm. In 1994, a team of researchers from the University of Minnesota and MIT built a recommendation system based on what they called “a deceptively simple idea”: people who agreed in the past are likely to agree again in the future. That notion led directly to the collaborative filtering systems that all self-respecting e-commerce sites have. Suppose that, like Netflix, you’ve gathered a database of movie ratings, with each user giving a rating of one to five stars to the movies he or she has seen. You want to decide whether your user Ken will like Gravity, so you find the users whose past ratings correlate most highly with his. If they all gave Gravity high ratings, then probably so will Ken, and you can recommend it to him. If they disagree on Gravity, however, you need a fallback point, which in this case is ranking users by how highly they correlate with Ken. So if Lee’s correlation with Ken is higher than Meg’s, his ratings should count for correspondingly more. Ken’s predicted rating is then the weighted average of his neighbors’, with each neighbor’s weight being his coefficient of correlation with Ken.

There’s an interesting twist, though. Suppose Lee and Ken have very similar tastes, but Lee is grumpier than Ken. Whenever Ken gives a movie five stars, Lee gives three; when Ken gives three, Lee gives one, and so on. We’d like to use Lee’s ratings to predict Ken’s, but if we just do it directly, we’ll always be off by two stars. Instead, what we need to do is predict how much Ken’s ratings will be above or below his average, based on how much Lee’s are. And now, since Ken is always two stars above his average when Lee is two stars above his, and so on, our predictions will be spot on.

You don’t need explicit ratings to do collaborative filtering, by the way. If Ken ordered a movie on Netflix, that means he expects to like it. So the “ratings” can just be ordered/not ordered, and two users are similar if they’ve ordered a lot of the same movies. Even just clicking on something implicitly shows interest in it. Nearest-neighbor works with all of the above. These days all kinds of algorithms are used to recommend items to users, but weighted k-nearest-neighbor was the first widely used one, and it’s still hard to beat.

Recommender systems, as they’re also called, are big business: a third of Amazon’s business comes from its recommendations, as does three-quarters of Netflix’s. It’s a far cry from the early days of nearest-neighbor, when it was considered impractical because of its memory requirements. Back then, computer memories were made of small iron rings, one per bit, and storing even a few thousand examples was taxing. How times have changed. Nevertheless, it’s not necessarily smart to remember all the examples you’ve seen and then have to search through them, particularly since most are probably irrelevant. If you look back at the map of Posistan and Negaland, you may notice that if Positiville disappeared, nothing would change. The metro areas of nearby cities would expand into the land formerly occupied by Positiville, but since they’re all Posistan cities, the border with Negaland would stay the same. The only cities that really matter are the ones across the border from a city in the other country; all others we can omit. So a simple way to make nearest-neighbor more efficient is to delete all the examples that are correctly classified by their neighbors. This and other tricks enable nearest-neighbor methods to be used in some surprising areas, like controlling robot arms in real time. But needless to say, they’re still not the first choice for things like high-frequency trading, where computers buy and sell stocks in fractions of a second. In a race between a neural network, which can be applied to an example with only a fixed number of additions, multiplications, and sigmoids and an algorithm that needs to search a large database for the example’s nearest neighbors, the neural network is sure to win.

Another reason researchers were initially skeptical of nearest-neighbor was that it wasn’t clear if it could learn the true borders between concepts. But in 1967 Tom Cover and Peter Hart proved that, given enough data, nearest-neighbor is at worst only twice as error-prone as the best imaginable classifier. If, say, at least 1 percent of test examples will inevitably be misclassified because of noise in the data, then nearest-neighbor is guaranteed to get at most 2 percent wrong. This was a momentous revelation. Up until then, all known classifiers assumed that the frontier had a very specific form, typically a straight line. This was a double-edged sword: on the one hand, it made proofs of correctness possible, as in the case of the perceptron, but it also meant that the classifier was strictly limited in what it could learn. Nearest-neighbor was the first algorithm in history that could take advantage of unlimited amounts of data to learn arbitrarily complex concepts. No human being could hope to trace the frontiers it forms in hyperspace from millions of examples, but because of Cover and Hart’s proof, we know that they’re probably not far off the mark. According to Ray Kurzweil, the Singularity begins when we can no longer understand what computers do. By that standard, it’s not entirely fanciful to say that it’s already under way-it began all the way back in 1951, when Fix and Hodges invented nearest-neighbor, the little algorithm that could.

The curse of dimensionality

There’s a serpent in this Eden, of course. It’s called the curse of dimensionality, and while it affects all learners to a greater or lesser degree, it’s particularly bad for nearest-neighbor. In low dimensions (like two or three), nearest-neighbor usually works quite well. But as the number of dimensions goes up, things fall apart pretty quickly. It’s not uncommon today to have thousands or even millions of attributes to learn from. For an e-commerce site trying to learn your preferences, every click you make is an attribute. So is every word on a web page, and every pixel on an image. But even with just tens or hundreds of attributes, chances are nearest-neighbor is already in trouble. The first problem is that most attributes are irrelevant: you may know a million factoids about Ken, but chances are only a few of them have anything to say about (for example) his risk of getting lung cancer. And while knowing whether he smokes is crucial for making that particular prediction, it’s probably not much help in deciding whether he’ll enjoy seeing Gravity. Symbolist methods, for one, are fairly good at disposing of irrelevant attributes. If an attribute has no information about the class, it’s just never included in the decision tree or rule set. But nearest-neighbor is hopelessly confused by irrelevant attributes because they all contribute to the similarity between examples. With enough irrelevant attributes, accidental similarity in the irrelevant dimensions swamps out meaningful similarity in the important ones, and nearest-neighbor becomes no better than random guessing.

A bigger problem is that, surprisingly, having more attributes can be harmful even when they’re all relevant. You’d think that more information is always better-isn’t that the motto of our age? But as the number of dimensions goes up, the number of training examples you need to locate the concept’s frontiers goes up exponentially. With twenty Boolean attributes, there are roughly a million different possible examples. With twenty-one, there are two million, and a corresponding number of ways the frontier could wind between them. Every extra attribute makes the learning problem twice as hard, and that’s just with Boolean attributes. If the attribute is highly informative, the benefit of adding it may exceed the cost. But if you have only weakly informative attributes, like the words in an e-mail or the pixels in an image, you’re probably in trouble, even though collectively they may have enough information to predict what you want.

It gets even worse. Nearest-neighbor is based on finding similar objects, and in high dimensions, the notion of similarity itself breaks down. Hyperspace is like the Twilight Zone. The intuitions we have from living in three dimensions no longer apply, and weird and weirder things start to happen. Consider an orange: a tasty ball of pulp surrounded by a thin shell of skin. Let’s say 90 percent of the radius of an orange is occupied by pulp, and the remaining 10 percent by skin. That means 73 percent of the volume of the orange is pulp (0.9³). Now consider a hyperorange: still with 90 percent of the radius occupied by pulp, but in a hundred dimensions, say. The pulp has shrunk to only about three thousandths of a percent of the hyperorange’s volume (0.9¹⁰⁰). The hyperorange is all skin, and you’ll never be done peeling it!

Another disturbing example is what happens with our good old friend, the normal distribution, aka a bell curve. What a normal distribution says is that data is essentially located at a point (the mean of the distribution), but with some fuzz around it (given by the standard deviation). Right? Not in hyperspace. With a high-dimensional normal distribution, you’re more likely to get a sample far from the mean than close to it. A bell curve in hyperspace looks more like a doughnut than a bell. And when nearest-neighbor walks into this topsy-turvy world, it gets hopelessly confused. All examples look equally alike, and at the same time they’re too far from each other to make useful predictions. If you sprinkle examples uniformly at random inside a high-dimensional hypercube, most are closer to a face of the cube than to their nearest neighbor. In medieval maps, uncharted areas were marked with dragons, sea serpents, and other fantastical creatures, or just with the phrase here be dragons. In hyperspace, the dragons are everywhere, including at your front door. Try to walk to your next-door neighbor’s house, and you’ll never get there; you’ll be forever lost in strange lands, wondering where all the familiar things went.

Decision trees are not immune to the curse of dimensionality either. Let’s say the concept you’re trying to learn is a sphere: points inside it are positive, and points outside it are negative. A decision tree can approximate a sphere by the smallest cube it fits inside. Not perfect, but not too bad either: only the corners of the cube get misclassified. But in high dimensions, almost the entire volume of the hypercube lies outside the hypersphere. For every example you correctly classify as positive, you incorrectly classify many negative ones as positive, causing your accuracy to plummet.

In fact, no learner is immune to the curse of dimensionality. It’s the second worst problem in machine learning, after overfitting. The term curse of dimensionality was coined by Richard Bellman, a control theorist, in the fifties. He observed that control algorithms that worked fine in three dimensions became hopelessly inefficient in higher-dimensional spaces, such as when you want to control every joint in a robot arm or every knob in a chemical plant. But in machine learning the problem is more than just computational cost-it’s that learning itself becomes harder and harder as the dimensionality goes up.

All is not lost, however. The first thing we can do is get rid of the irrelevant dimensions. Decision trees do this automatically by computing the information gain of each attribute and using only the most informative ones. For nearest-neighbor, we can accomplish something similar by first discarding all attributes whose information gain is below some threshold and then measuring similarity only in the reduced space. This is quick and good enough for some applications, but unfortunately it precludes learning many concepts, like exclusive-OR: if an attribute only says something about the class when combined with others, but not on its own, it will be discarded. A more expensive but smarter option is to “wrap” the attribute selection around the learner itself, with a hill-climbing search that keeps deleting attributes as long as that doesn’t hurt nearest-neighbor’s accuracy on held-out data. Newton did a lot of attribute selection when he decided that all that matters for predicting an object’s trajectory is its mass-not its color, smell, age, or myriad other properties. In fact, the most important thing about an equation is all the quantities that don’t appear in it: once we know what the essentials are, figuring out how they depend on each other is often the easier part.

To handle weakly relevant attributes, one option is to learn attribute weights. Instead of letting the similarity along all dimensions count equally, we “shrink” the less-relevant ones. Suppose the training examples are points in a room, and the height dimension is not that important for our purposes. Discarding it would project all examples onto the floor. Downweighting it is more like giving the room a lower ceiling. The height of a point still counts when computing its distance to other points, but less than its horizontal position. And like many other things in machine learning, we can learn attribute weights by gradient descent.

It may happen that the room has a high ceiling, but the data points are all near the floor, like a thin layer of dust settling on the carpet. In that case, we’re in luck: the problem looks three dimensional, but in effect it’s closer to two dimensional. We don’t have to shrink height because nature has already shrunk it for us. This “blessing of nonuniformity,” whereby data is not spread uniformly in (hyper) space, is often what saves the day. The examples may have a thousand attributes, but in reality they all “live” in a much lower-dimensional space. That’s why nearest-neighbor can be good for handwritten digit recognition, for example: each pixel is a dimension, so there are many, but only a tiny fraction of all possible images are digits, and they all live together in a cozy little corner of hyperspace. The shape of the lower-dimensional space the data lives in may be quite capricious, however. For example, if a room has furniture in it, the dust doesn’t just settle on the floor; it settles on the tabletops, chair seats, bed covers, and whatnot. If we can figure out the approximate shape of the blanket of dust covering the room, then all we need is each point’s coordinates on it. As we’ll see in the next chapter, there’s a whole subfield of machine learning dedicated to, so to speak, discovering blanket shapes by groping around in the darkness of hyperspace.

Snakes on a plane

Up until the mid-1990s, the most widely used analogical learner was nearest-neigbhor, but it was overshadowed by its more glamorous cousins from the other tribes. But then a new similarity-based algorithm burst onto the scene, sweeping all before it. In fact, you could say it was another “peace dividend” from the end of the Cold War. Support vector machines, or SVMs for short, were the brainchild of Vladimir Vapnik, a Soviet frequentist. Vapnik spent most of his career at the Institute of Control Sciences in Moscow, but in 1990, as the Soviet Union unraveled, he emigrated to the United States, where he joined the legendary Bell Labs. While in Russia, Vapnik had been mostly content to do theoretical, pencil-and-paper work, but the atmosphere at Bell Labs was different. Researchers were looking for practical results, and Vapnik finally decided to turn his ideas into an algorithm. Within a few years, he and his colleagues at Bell Labs had developed SVMs, and before long they were everywhere, setting new accuracy records left and right.

Superficially, an SVM looks a lot like weighted k-nearest-neighbor: the frontier between the positive and negative classes is defined by a set of examples and their weights, together with a similarity measure. A test example belongs to the positive class if, on average, it looks more like the positive examples than the negative ones. The average is weighted, and the SVM remembers only the key examples required to pin down the frontier. If you look back at the Posistan/Negaland example, once we throw away all the towns that aren’t on the border, all that’s left is this map:

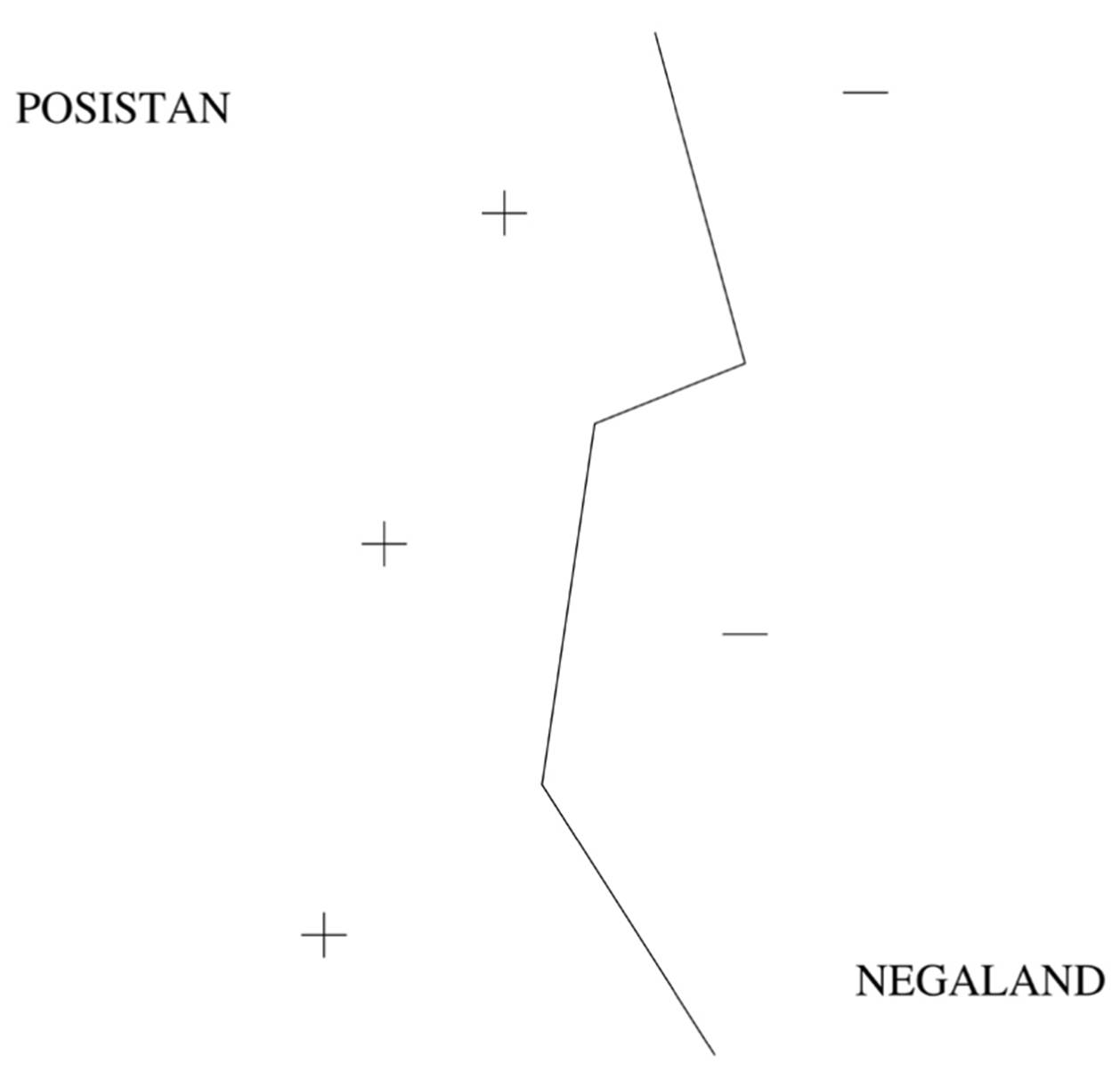
These examples are called support vectors because they’re the vectors that “hold up” the frontier: remove one, and a section of the frontier slides to a different place. You may also notice that the frontier is a jagged line, with sudden corners that depend on the exact location of the examples. Real concepts tend to have smoother borders, which means nearest-neighbor’s approximation is probably not ideal. But with SVMs, we can learn smooth frontiers, more like this:

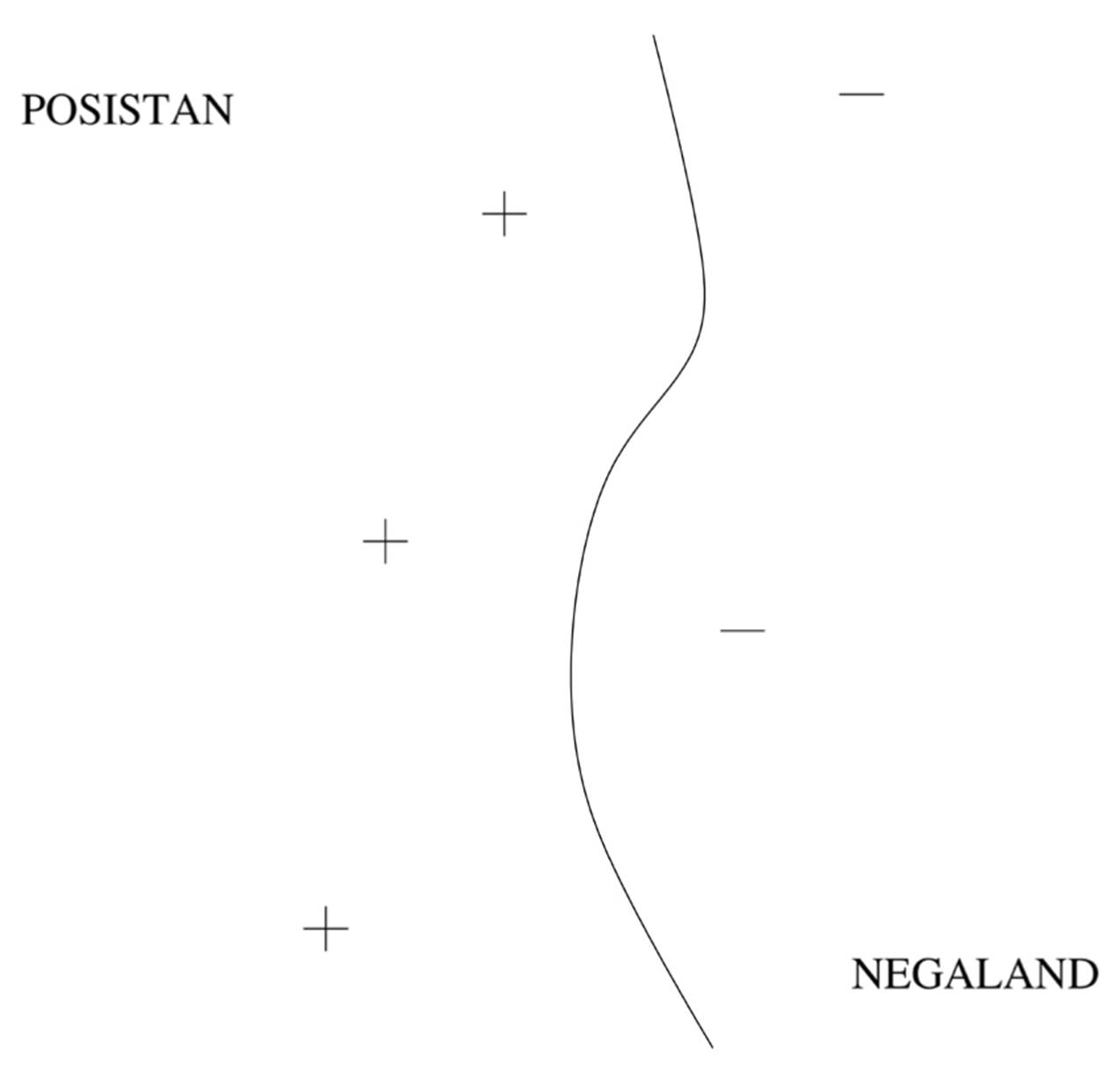
To learn an SVM, we need to choose the support vectors and their weights. The similarity measure, which in SVM-land is called the kernel, is usually chosen a priori. One of Vapnik’s key insights was that not all borders that separate the positive training examples from the negative ones are created equal. Suppose Posistan and Negaland are at war, and they’re separated by a no-man’s-land with minefields on either side. Your mission is to survey the no-man’s-land, walking from one end of it to the other without stepping on any mines. Luckily, you have a map of where the mines are buried. Obviously, you don’t just take any old path: you give the mines the widest possible berth. That’s what SVMs do, with the examples as mines and the learned border as the chosen path. The closest the border ever comes to an example is its margin of safety, and the SVM chooses the support vectors and weights that yield the maximum possible margin. For example, the solid straight-line border in this figure is better than the dotted one:

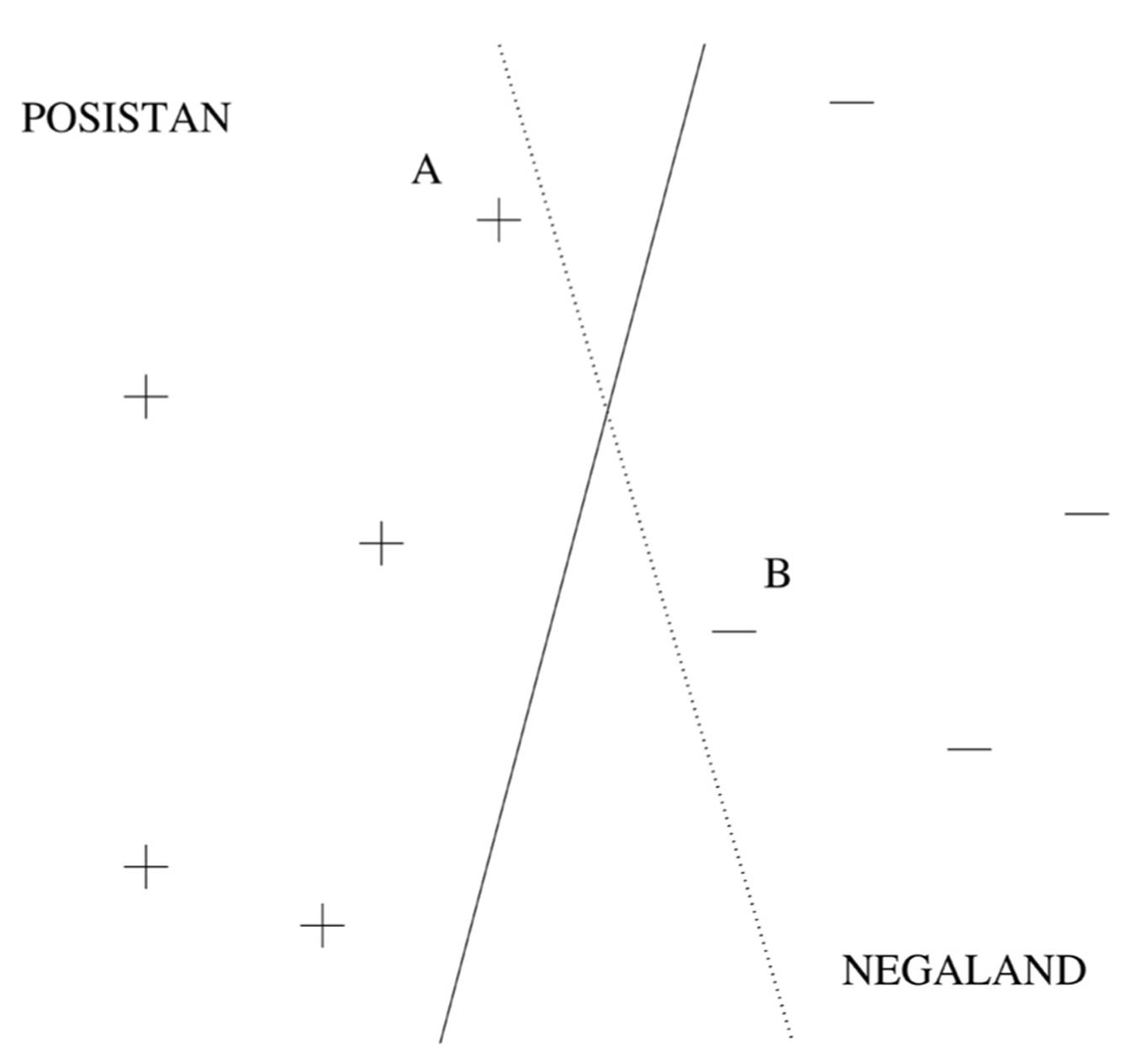
The dotted border separates the positive and negative examples just fine, but it comes dangerously close to stepping on the landmines at A and B. These examples are support vectors: delete one of them, and the maximum-margin border moves to a different place. In general, the border can be curved, of course, making the margin harder to visualize, but we can think of the border as a snake slithering down the no-man’s-land, and the margin is how fat the snake can be. If a very fat snake can slither all the way down without blowing itself to smithereens, then the SVM can separate the positive and negative examples very well, and Vapnik showed that in this case we can be confident that the SVM didn’t overfit. Intuitively, compared to a thin snake, there are fewer ways a fat snake can slither down while avoiding the landmines; and likewise, compared to a low-margin SVM, a high-margin one has fewer chances of overfitting by drawing an overly intricate border.

The second part of the story is how the SVM finds the fattest snake that fits between the positive and negative landmines. At first sight, it might seem like learning a weight for each training example by gradient descent would do the trick. All we have to do is find the weights that maximize the margin, and any examples that end up with zero weight can be discarded. Unfortunately, this would just make the weights grow without limit, because mathematically, the larger the weights, the larger the margin. If you’re one foot from a landmine and you double the size of everything including yourself, you are now two feet from the landmine, but that doesn’t make you any less likely to step on it. Instead, we have to maximize the margin under the constraint that the weights can only increase up to some fixed value. Or, equivalently, we can minimize the weights under the constraint that all examples have a given margin, which could be one-the precise value is arbitrary. This is what SVMs usually do.

Constrained optimization is the problem of maximizing or minimizing a function subject to constraints. The universe maximizes entropy subject to keeping energy constant. Problems of this type are widespread in business and technology. For example, we may want to maximize the number of widgets a factory produces, subject to the number of machine tools available, the widgets’ specs, and so on. With SVMs, constrained optimization became crucial for machine learning as well. Unconstrained optimization is getting to the top of the mountain, and that’s what gradient descent (or, in this case, ascent) does. Constrained optimization is going as high as you can while staying on the road. If the road goes up to the very top, the constrained and unconstrained problems have the same solution. More often, though, the road zigzags up the mountain and then back down without ever reaching the top. You know you’ve reached the highest point on the road when you can’t go any higher without driving off the road; in other words, when the path to the top is at right angles to the road. If the road and the path to the top form an oblique angle, you can always get higher by driving farther along the road, even if that doesn’t get you higher as quickly as aiming straight for the top of the mountain. So the way to solve a constrained optimization problem is to follow not the gradient but the part of it that’s parallel to the constraint surface-in this case the road-and stop when that part is zero.

In general, we have to deal with many constraints at once (one per example, in the case of SVMs). Suppose you wanted to get as close as possible to the North Pole but couldn’t leave your room. Each of the room’s four walls is a constraint, and the solution is to follow the compass until you bump into the corner where the northeast and northwest walls meet. We say that these two walls are the active constraints because they’re what prevents you from reaching the optimum, namely the North Pole. If your room has a wall facing exactly north, that’s the sole active constraint, and the solution is a point in the middle of it. And if you’re Santa and your room is already over the North Pole, all constraints are inactive, and you can just sit there pondering the optimal toy distribution problem instead. (Traveling salesmen have it easy compared to Santa.) In an SVM, the active constraints are the support vectors since their margin is already the smallest it’s allowed to be; moving the frontier would violate one or more constraints. All other examples are irrelevant, and their weight is zero.

In reality, we usually let SVMs violate some constraints, meaning classify some examples incorrectly or by less than the margin, because otherwise they would overfit. If there’s a noisy negative example somewhere in the middle of the positive region, we don’t want the frontier to wind around inside the positive region just to get that example right. But the SVM pays a penalty for each example it gets wrong, which encourages it to keep those to a minimum. SVMs are like the sandworms in Dune: big, tough, and able to survive a few explosions from slithering over landmines but not too many.

Looking around for applications, Vapnik and his coworkers soon alighted on handwritten digit recognition, which their connectionist colleagues at Bell Labs were the world experts on. To everyone’s surprise, SVMs did as well out of the box as multilayer perceptrons that had been carefully crafted for digit recognition over the years. This set the stage for a long-running, wide-ranging competition between the two. SVMs can be seen as a generalization of the perceptron, because a hyperplane boundary between classes is what you get when you use a particular similarity measure (the dot product between vectors). But SVMs have a major advantage compared to multilayer perceptrons: the weights have a single optimum instead of many local ones and so learning them reliably is much easier. Despite this, SVMs are no less expressive than multilayer perceptrons; the support vectors effectively act as a hidden layer and their weighted average as the output layer. For example, an SVM can easily represent the exclusive-OR function by having one support vector for each of the four possible configurations. But the connectionists didn’t give up without a fight. In 1995, Larry Jackel, the head of Vapnik’s department at Bell Labs, bet him a fancy dinner that by 2000 neural networks would be as well understood as SVMs. He lost. But in return, Vapnik bet that by 2005 no one would use neural networks any more, and he also lost. (The only one to get a free dinner was Yann LeCun, their witness.) Moreover, with the advent of deep learning, connectionists have regained the upper hand. Provided you can learn them, networks with many layers can express many functions more compactly than SVMs, which always have just one layer, and this can make all the difference.

Another notable early success of SVMs was in text classification, which proved a major boon because the web was then just taking off. At the time, Na?ve Bayes was the state-of-the-art text classifier, but when every word in the language is a dimension, even it can start to overfit. All it takes is a word that, by chance, occurs in, say, all sports pages in the training data and no others, and Na?ve Bayes starts to hallucinate that every page containing that word is a sports page. But, thanks to margin maximization, SVMs can resist overfitting even in very high dimensions.

Generally, the fewer support vectors an SVM selects, the better it generalizes. Any training example that is not a support vector would be correctly classified if it showed up as a test example instead because the frontier between positive and negative examples would still be in the same place. So the expected error rate of an SVM is at most the fraction of examples that are support vectors. As the number of dimensions goes up, this fraction tends to go up as well, so SVMs are not immune to the curse of dimensionality. But they’re more resistant to it than most.

Practical successes aside, SVMs also turned a lot of machine-learning conventional wisdom on its head. For example, they gave the lie to the notion, sometimes misidentified with Occam’s razor, that simpler models are more accurate. On the contrary, an SVM can have an infinite number of parameters and still not overfit, provided it has a large enough margin.

The single most surprising property of SVMs, however, is that no matter how curvy the frontiers they form, those frontiers are always just straight lines (or hyperplanes, in general). The reason that’s not a contradiction is that the straight lines are in a different space. Suppose the examples live on the (x,y) plane, and the boundary between the positive and negative regions is the parabola y = x². There’s no way to represent it with a straight line, but if we add a third coordinate z, meaning the data now lives in (x,y,z) space, and we set each example’s z coordinate to the square of its x coordinate, the frontier is now just the diagonal plane defined by y = z. In effect, the data points rise up into the third dimension, some rise more than others by just the right amount, and presto-in this new dimension the positive and negative examples can be separated by a plane. It turns out that we can view what SVMs do with kernels, support vectors, and weights as mapping the data to a higher-dimensional space and finding a maximum-margin hyperplane in that space. For some kernels, the derived space has infinite dimensions, but SVMs are completely unfazed by that. Hyperspace may be the Twilight Zone, but SVMs have figured out how to navigate it.

Climbing the ladder

Two things are similar if they agree with one another in some respects. If they agree in some respects, they will probably also agree in others. This is the essence of analogy. It also points to the two main subproblems in analogical reasoning: figuring out how similar two things are and deciding what else to infer from their similarities. So far we’ve explored the “low power” end of analogy, with algorithms like nearest-neighbor and SVMs, where the answers to both these questions are very simple. They’re the most widely used, but a chapter on analogical learning would not be complete without at least a whirlwind tour of the more powerful parts of the spectrum.

The most important question in any analogical learner is how to measure similarity. It could be as simple as Euclidean distance between data points, or as complex as a whole program with multiple levels of subroutines whose final output is a similarity value. Either way, the similarity function controls how the learner generalizes from known examples to new ones. It’s where we insert our knowledge of the problem domain into the learner, making it the analogizers’ answer to Hume’s question. We can apply analogical learning to all kinds of objects, not just vectors of attributes, provided we have a way of measuring the similarity between them. For example, we can measure the similarity between two molecules by the number of identical substructures they contain. Methane and methanol are similar because they have three carbon-hydrogen bonds in common and differ only in the replacement of a hydrogen atom by a hydroxyl group:

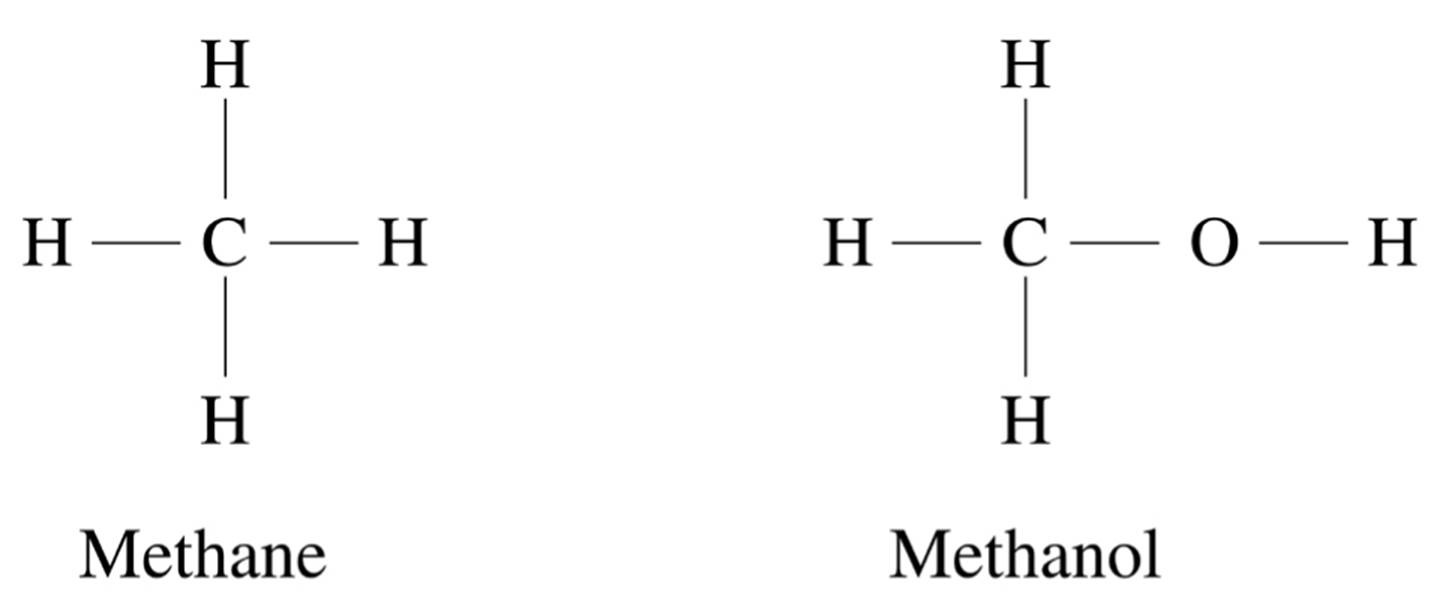
However, that doesn’t mean their chemical behavior is similar. Methane is a gas, while methanol is an alcohol. The second part of analogical reasoning is figuring out what we can infer about the new object based on similar ones we’ve found. This can be very simple or very complex. In nearest-neighbor or SVMs, it just consists of predicting the new object’s class based on the classes of the nearest neighbors or support vectors. But in case-based reasoning, another type of analogical learning, the output can be a complex structure formed by composing parts of the retrieved objects. Suppose your HP printer is spewing out gibberish, and you call up their help desk. Chances are they’ve seen your problem many times before, so a good strategy is to find those records and piece together a potential solution for your problem from them. This is not just a matter of finding complaints with many similar attributes to yours: for example, whether you’re using your printer with Windows or Mac OS X may cause very different settings of the system and the printer to become relevant. And once you’ve found the most relevant cases, the sequence of steps needed to solve your problem may be a combination of steps from different cases, with some further tweaks specific to yours.

Help desks are currently the most popular application of case-based reasoning. Most still employ a human intermediary, but IPsoft’s Eliza talks directly to the customer. Eliza, who comes complete with a 3-D interactive video persona, has solved over twenty million customer problems to date, mostly for blue-chip US companies. “Greetings from Robotistan, outsourcing’s cheapest new destination,” is how an outsourcing blog recently put it. And, just as outsourcing keeps climbing the skills ladder, so does analogical learning. The first robo-lawyers that argue for a particular verdict based on precedents have already been built. One such system correctly predicted the outcomes of over 90 percent of the trade secret cases it examined. Perhaps in a future cyber-court, in session somewhere on Amazon’s cloud, a robo-lawyer will beat the speeding ticket that RoboCop issued to your driverless car, all while you go to the beach, and Leibniz’s dream of reducing all argument to calculation will finally have come true.

Arguably even higher up in the skills ladder is music composition. David Cope, an emeritus professor of music at the University of California, Santa Cruz, designed an algorithm that creates new music in the style of famous composers by selecting and recombining short passages from their work. At a conference I attended some years ago, he played three “Mozart” pieces: one by the real Mozart, one by a human composer imitating Mozart, and one by his system. He then asked the audience to vote for the authentic Amadeus. Wolfgang won, but the computer beat the human imitator. This being an AI conference, the audience was delighted. Audiences at other events were less happy. One listener angrily accused Cope of ruining music for him. If Cope is right, creativity-the ultimate unfathomable-boils down to analogy and recombination. Judge for yourself by googling “david cope mp3.”

Analogizers’ neatest trick, however, is learning across problem domains. Humans do it all the time: an executive can move from, say, a media company to a consumer-products one without starting from scratch because many of the same management skills still apply. Wall Street hires lots of physicists because physical and financial problems, although superficially very different, often have a similar mathematical structure. Yet all the learners we’ve seen so far would fall flat if we, say, trained them to predict Brownian motion and then asked them to predict the stock market. Stock prices and the velocities of particles suspended in a fluid are just different variables, so the learner wouldn’t even know where to start. But analogizers can do this using structure mapping, an algorithm invented by Dedre Gentner, a psychologist at Northwestern University. Structure mapping takes two descriptions, finds a coherent correspondence between some of their parts and relations, and then, based on that correspondence, transfers further properties from one structure to the other. For example, if the structures are the solar system and the atom, we can map planets to electrons and the sun to the nucleus and conclude, as Bohr did, that electrons revolve around the nucleus. The truth is more subtle, of course, and we often need to refine analogies after we make them. But being able to learn from a single example like this is surely a key attribute of a universal learner. When we’re confronted with a new type of cancer-and that happens all the time because cancers keep mutating-the models we’ve learned for previous ones don’t apply. Neither do we have time to gather data on the new cancer from a lot of patients; there may be only one, and she urgently needs a cure. Our best hope is then to compare the new cancer with known ones and try to find one whose behavior is similar enough that some of the same lines of attack will work.

Is there anything analogy can’t do? Not according to Douglas Hofstadter, cognitive scientist and author of G?del, Escher, Bach: An Eternal Golden Braid. Hofstadter, who looks a bit like the Grinch’s good twin, is probably the world’s best-known analogizer. In their book Surfaces and Essences: Analogy as the Fuel and Fire of Thinking, Hofstadter and his collaborator Emmanuel Sander argue passionately that all intelligent behavior reduces to analogy. Everything we learn or discover, from the meaning of everyday words like mother and play to the brilliant insights of geniuses like Albert Einstein and ?variste Galois, is the result of analogy in action. When little Tim sees women looking after other children like his mother looks after him, he generalizes the concept “mommy” to mean anyone’s mommy, not just his. That in turn is a springboard for understanding things like “mother ship” and “Mother Nature.” Einstein’s “happiest thought,” out of which grew the general theory of relativity, was an analogy between gravity and acceleration: if you’re in an elevator, you can’t tell whether your weight is due to one or the other because their effects are the same. We swim in a vast ocean of analogies, which we both manipulate for our ends and are unwittingly manipulated by. Books have analogies on every page (like the title of this section, or the previous one’s). G?del, Escher, Bach is an extended analogy between G?del’s theorem, Escher’s art, and Bach’s music. If the Master Algorithm is not analogy, it must surely be something like it.

Rise and shine

Cognitive science has seen a long-running debate between symbolists and analogizers. Symbolists point to something they can model that analogizers can’t; then analogizers figure out how to do it, come up with something they can model that symbolists can’t, and the cycle repeats. Instance-based learning, as it’s sometimes called, is supposedly better for modeling how we remember specific episodes in our lives; rules are the putative choice for reasoning with abstract concepts like “work” and “love.” But when I was a graduate student, it struck me that these two are really just points on a continuum, and we should be able to learn across all of it. Rules are in effect generalized instances where we’ve “forgotten” some attributes because they didn’t matter. Conversely, instances are very specific rules, with a condition on every attribute. As we go through life, similar episodes gradually become abstracted into rule-based structures, like “eating at a restaurant.” You know that going to a restaurant involves ordering from a menu and leaving a tip, and you follow those “rules of conduct” every time you eat out, but you probably don’t remember the specific restaurants where you first became aware of them.

In my PhD thesis, I designed an algorithm that unifies instance-based and rule-based learning in this way. A rule doesn’t just match entities that satisfy all its preconditions; it matches any entity that’s more similar to it than to any other rule, in the sense that it comes closer to satisfying its conditions. For instance, someone with a cholesterol level of 220 mg/dL comes closer than someone with 200 mg/dL to matching the rule If your cholesterol is above 240 mg/dL, you’re at risk of a heart attack. RISE, as I called the algorithm, learns by starting with each training example as a rule and then gradually generalizing each rule to absorb the nearest examples. The end result is usually a combination of very general rules, which between them match most examples, with more specific rules that match exceptions to those, and so on all the way to a “long tail” of specific memories. RISE made better predictions than the best rule-based and instance-based learners of the time, and my experiments showed that this was precisely because it combined the best features of both. Rules can be matched analogically, and so they’re no longer brittle. Instances can select different features in different regions of space and so combat the curse of dimensionality much better than nearest-neighbor, which can only select the same features everywhere.

RISE was a step toward the Master Algorithm because it combined symbolic and analogical learning. It was only a small step, however, because it doesn’t have the full power of either of those paradigms, and it’s still missing the other three. RISE’s rules can’t be chained together in different ways; each rule just predicts the class of an example directly from its attributes. Also, the rules can’t talk about more than one entity at a time; for example, RISE can’t express a rule like If A has the flu and B was in contact with A, B may have the flu as well. On the analogical side, RISE just generalizes the simple nearest-neighbor algorithm; it can’t learn across domains using structure mapping or some such strategy. At the time I finished my PhD, I didn’t see a way to bring together in one algorithm the full power of all the five paradigms, and I set the problem aside for a while. But as I applied machine learning to problems like word-of-mouth marketing, data integration, programming by example, and website personalization, I kept seeing how each of the paradigms provided only part of the solution. There had to be a better way.

And so we have traveled through the territories of the five tribes, gathering their insights, negotiating the border crossings, wondering how the pieces might fit together. We know immensely more now than when we started out. But something is still missing. There’s a gaping hole in the center of the puzzle, making it hard to see the pattern. The problem is that all the learners we’ve seen so far need a teacher to tell them the right answer. They can’t learn to distinguish tumor cells from healthy ones unless someone labels them “tumor” or “healthy.” But humans can learn without a teacher; they do it from the day they’re born. Like Frodo at the gates of Mordor, our long journey will have been in vain if we don’t find a way around this barrier. But there is a path past the ramparts and the guards, and the prize is near. Follow me…

Оглавление книги