Книга: Учебное пособие по курсу «Нейроинформатика»

Функционирование сети

Функционирование сети

Сеть работает следующим образом:

1. На вход сети подается образ x, а на выходе снимается образ x'.

2. Если x' ? x, то полагаем x = x' и возвращаемся к шагу 1.

3. Полученный вектор x' является ответом.

Таким образом, ответ всегда является неподвижной точкой преобразования сети (2) и именно это условие (неизменность при обработке образа сетью) и является условием остановки.

Пусть j^* — номер эталона, ближайшего к образу x. Тогда, если выбрать веса пропорционально близости эталонов к исходному образу x, то следует ожидать, что образ x' будет ближе к эталону x^i?, чем x, а после нескольких итераций он станет совпадать с эталоном x^i?.

Наиболее простой сетью вида (2) является дискретный вариант сети Хопфилда [312] с весами равными скалярному произведению эталонов на предъявляемый образ:

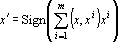
Рис. 1. а, б, в — эталоны, г — ответ сети на предъявление любого эталона

О сетях Хопфилда (3) известно [53, 231, 247, 312], что они способны запомнить и точно воспроизвести «порядка 0.14n слабо коррелированных образов». В этом высказывании содержится два ограничения:

• число эталонов не превосходит 0.14n.

• эталоны слабо коррелированны.

Наиболее существенным является второе ограничение, поскольку образы, которые сеть должна обрабатывать, часто очень похожи. Примером могут служить буквы латинского алфавита. При обучении сети Хопфилда (3) распознаванию трех первых букв (см. рис. 1 а, б, в), при предъявлении на вход сети любого их эталонов в качестве ответа получается образ, приведенный на рис. 1 г (все образы брались в рамке 10 на 10 точек).

В связи с такими примерами первый вопрос о качестве работы сети ассоциативной памяти звучит тривиально: будет ли сеть правильно обрабатывать сами эталонные образы (т. е. не искажать их)?

Мерой коррелированности образов будем называть следующую величину:

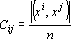
Зависимость работы сети Хопфилда от степени коррелированности образов можно легко продемонстрировать на следующем примере. Пусть даны три эталона x¹, x², x³ таких, что

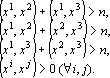
Для любой координаты существует одна из четырех возможностей:

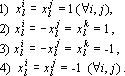
В первом случае при предъявлении сети q-го эталона в силу формулы (3) получаем

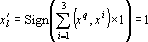
так как все скалярные произведения положительны по условию (4). Аналогично получаем в четвертом случае x'_j = -1.

Во втором случае рассмотрим отдельно три варианта

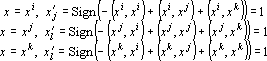
так как скалярный квадрат любого образа равен n, а сумма двух любых скалярных произведений эталонов больше n, по условию (4). Таким образом, независимо от предъявленного эталона получаем x'_j = 1. Аналогично в третьем случае получаем x'_j = -1.

Окончательный вывод таков: если эталоны удовлетворяют условиям (4), то при предъявлении любого эталона на выходе всегда будет один образ. Этот образ может быть эталоном или «химерой», составленной, чаще всего, из узнаваемых фрагментов различных эталонов (примером «химеры» может служить образ, приведенный на рис. 1 г). Рассмотренный ранее пример с буквами детально иллюстрирует такую ситуацию.

Приведенные выше соображения позволяют сформулировать требование, детализирующие понятие «слабо коррелированных образов». Для правильного распознавания всех эталонов достаточно (но не необходимо) потребовать, чтобы выполнялось следующее неравенство

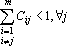
Более простое и наглядное, хотя и более сильное условие можно записать в виде

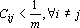
Из этих условий видно, что, чем больше задано эталонов, тем более жесткие требования предъявляются к степени их коррелированности, тем ближе они должны быть к ортогональным.

Рассмотрим преобразование (3) как суперпозицию двух преобразований:

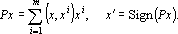
Обозначим через

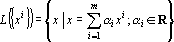
— линейное пространство, натянутое на множество эталонов. Тогда первое преобразование в (5) переводит векторы из Rnв L({xⁱ}). Второе преобразование в (5) переводит результат первого преобразования Px в одну из вершин гиперкуба образов. Легко показать, что второе преобразование в (5) переводит точку Px в ближайшую вершину гиперкуба. Действительно, пусть a и b две различные вершины гиперкуба такие, что a — ближайшая к Px, а b = x'.

Из того, что a и b различны следует, что существует множество индексов, в которых координаты векторов a и b различны. Обозначим это множество через I = {i : a_i = -b_i}. Из второго преобразования в (5) и того, что b = x', следует, что знаки координат вектора Px всегда совпадают со знаками соответствующих координат вектора b. Учитывая различие знаков i-х координат векторов a и Px при i ? I можно записать |a_i-(Px)_i| = |a_i|+|(Px)_i| = 1+|(Px)_i|. Совпадение знаков i-х координат векторов b и Px при i ? I позволяет записать следующее неравенство |b_i-(Px)_i| = ||b_i|-|(Px)_i| < 1+|(Px)_i|. Сравним расстояния от вершин a и b до точки Px

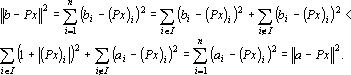
Полученное неравенство

Оглавление книги