Книга: Учебное пособие по курсу «Нейроинформатика»

Доказательство теоремы

Доказательство теоремы

В данном разделе приведено доказательство теоремы о числе линейно независимых образов в пространстве k-х тензорных степеней эталонов.

При построении тензорных сетей используются тензоры валентности k следующего вида:

(13)

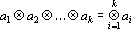
где a_j — n-мерные вектора над полем действительных чисел.

Если все вектора a_i=a, то будем говорить о k-й тензорной степени вектора a, и использовать обозначение a^?k. Для дальнейшего важны следующие элементарные свойства тензоров вида (13).

1. Пусть

и
, тогда скалярное произведение этих векторов может быть вычислено по формуле

(14)

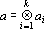
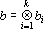
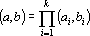
Доказательство этого свойства следует непосредственно из свойств тензоров общего вида.

2. Если в условиях свойства 1 вектора являются тензорными степенями, то скалярное произведение имеет вид:

(15)

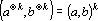
Доказательство непосредственно вытекает из свойства 1.

3. Если вектора a и b ортогональны, то есть (a,b) = 0, то и их тензорные степени любой положительной валентности ортогональны.

Доказательство вытекает из свойства 2.

4. Если вектора a и b коллинеарны, то есть b = ?a, то a^?k=?^ka^?k.

Следствие. Если множество векторов

содержит хотя бы одну пару противоположно направленных векторов, то система векторов
будет линейно зависимой при любой валентности k.

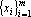
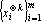
5. Применение к множеству векторов

невырожденного линейного преобразования B в пространстве Rnэквивалентно применению к множеству векторов
линейного невырожденного преобразования, индуцированного преобразованием B, в пространстве
.

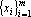
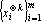
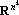
Сюръективным мультииндексом ?(L) над конечным множеством L назовем k-мерный вектор, обладающий следующими свойствами:

1. для любого iL существует j?{1, …, k} такое, что ?_j=i;

2. для любого j?{1, …, k} существует i?L такое, что ?_j=i.

Обозначим через d(?(L),i) число компонент сюръективного мультииндекса ?(L) равных i, через |L| — число элементов множества L, а через ?(L) — множество всех сюръективных мультииндексов над множеством L.

Предложение 1. Если вектор a представлен в виде

, где ?_i — произвольные действительные коэффициенты, то верно следующее равенство

(16)

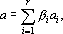
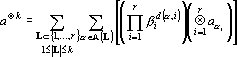
Доказательство предложения получается возведением

в тензорную степень k и раскрытием скобок с учетом линейности операции тензорного умножения.

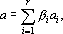
В множестве

, выберем множество X следующим образом: возьмем все (n-1)-мерные вектора с координатами ±1, а в качестве n-й координаты во всех векторах возьмем единицу.

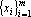
Предложение 2. Множество x является максимальным множеством n-мерных векторов с координатами равными ±1 и не содержит пар противоположно направленных векторов.

Доказательство. Из равенства единице последней координаты всех векторов множества X следует отсутствие пар противоположно направленных векторов. Пусть x — вектор с координатами ±1, не входящий в множество X, следовательно последняя координата вектора x равна минус единице. Так как в множество X включались все (n-1) — мерные вектора с координатами ±1, то среди них найдется вектор, первые n-1 координата которого равны соответствующим координатам вектора x со знаком минус. Поскольку последние координаты также имеют противоположные знаки, то в множестве X нашелся вектор противоположно направленный по отношению к вектору x. Таким образом множество X максимально.

Таким образом в множестве X содержится ровно 2^n-1 вектор. Каждый вектор x?X можно представить в виде

, где I?{1, …, n-1}. Для нумерации векторов множества X будем использовать мультииндекс I. Обозначим через |I| число элементов в мультииндексе I. Используя введенные обозначения можно разбить множество X на n непересекающихся подмножеств: P_i = {x_I, |I|=i},
.

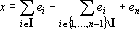
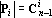
Теорема. При k<n в множестве {x^?k} линейно независимыми являются

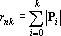
векторов.

Для доказательства этой теоремы потребуется следующая интуитивно очевидная, но не встреченная в литературе лемма.

Лемма. Пусть дана последовательность векторов

a₁,a₂=a?₂+a?₂,a₃=a?₃+a?₃,…,a_m=a?_m+a?_m

таких, что (a_i,a?_j)=0 при всех i<j и (a?_i,a?_i)=0, a?_i?0 при всех i, тогда все вектора множества {a_i} линейно независимы.

Доказательство. Известно, что процедура ортогонализации Грама приводит к построению ортонормированного множества векторов, а все вектора линейно зависящие от предыдущих векторов последовательности обращаются в нулевые. Проведем процедуру ортогонализации для заданной последовательности векторов.

1. b₁=a₁/||a₁||

2. b₂=(a₂-(a₂,b₂))/||a₂-(a₂,b₁)b₁||. Причем a₂-(a₂,b₁)b₁ ? 0, так как (a₁, a?₂)=0, (a?₂-((a₂,b₁)b₁,a?₂)=0 и a?₂?0.

…

j.

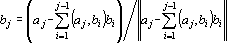
Причем

, так как (a_i, a?_j)=0, при всех i<j,

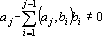
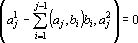
и a?_j?0.

…

Доказательство теоремы. Произведем линейное преобразование векторов множества x с матрицей

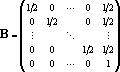
Легко заметить, что при этом преобразовании все единичные координаты переходят в единичные, а координаты со значением –1 в нулевые. Таким образом

.

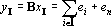
По пятому свойству заключаем, что число линейно независимых векторов в множествах X и Y совпадает. Пусть 1?m?k. Докажем, что y_I^?k при |I|=m содержит компоненту, ортогональную всем y_J^?k, |J|?m, J?I.

Из предложения 1 имеем

(17)

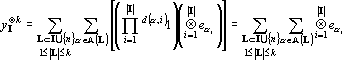
Представим (17) в виде двух слагаемых:

(18)

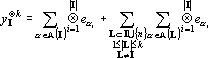
Обозначим первую сумму в (18) через y_I0^?k. Докажем, что y_I0^?k ортогонален ко всем y_J^?k, |J|?m, J?I, и второй сумме в (18). Так как I?J, I?J, существует q?I, q?J.

Из свойств сюръективного мультииндекса следует, что все слагаемые, входящие в y_I0^?k содержат в качестве тензорного сомножителя e_q, не входящий ни в одно тензорное произведение, составляющие в сумме y_J^?k. Из свойства 2 получаем, что (y_J^?k, y_I0^?k) = 0. Аналогично, из того, что в каждом слагаемом второй суммы L?I, I?L следует ортогональность y_I0^?k каждому слагаемому второй суммы в (18) и, следовательно, всей сумме.

Таким образом y_I^?k содержит компоненту y_I0^?k ортогональную ко всем y_J^?k, |J|?m, J?I и (y_J^?k-y_I0^?k). Множество тензоров Y_k={y_I^?k, |I|?k} удовлетворяет условиям леммы, и следовательно все тензоры в Y_k линейно независимы. Таким образом, число линейно независимых тензоров в множестве  не меньше чем

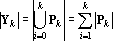
Для того, чтобы показать, что число линейно независимых тензоров в множестве {x^?k} не превосходит этой величины достаточно показать, что добавление любого тензора из Y к Y_k приводит к появлению линейной зависимости. Покажем, что любой y_I^?k при |I|>k может быть представлен в виде линейной комбинации тензоров из Y_k. Ранее было показано, что любой тензор y_I^?k может быть представлен в виде (17). Разобьем (17) на три суммы:

(19)

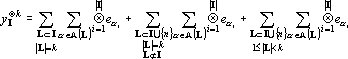
Рассмотрим первое слагаемое в (19) отдельно.

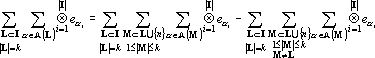
Заменим в последнем равенстве внутреннюю сумму в первом слагаемом на тензоры из Y_k:

(20)

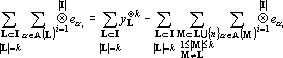
Преобразуем второе слагаемое в (19).

(21)

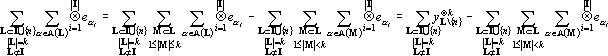
Преобразуя аналогично (21) второе слагаемое в (20) и подставив результаты преобразований в (19) получим

(22)

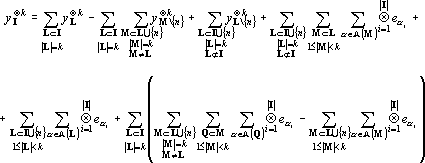
В (22) все не замененные на тензоры из Y_k слагаемые содержат суммы по подмножествам множеств мощностью меньше k. Проводя аналогичную замену получим выражение, содержащее суммы по подмножествам множеств мощностью меньше k-1 и так далее. После завершения процедуры в выражении останутся только суммы содержащие вектора из Y_k, то есть y_I^?k будет представлен в виде линейной комбинации векторов из Y_k. Теорема доказана.