Книга: Учебное пособие по курсу «Нейроинформатика»

Сети Хопфилда

Сети Хопфилда

Наиболее известной сетью ассоциативной памяти является сеть Хопфилда [312]. В основе сети Хопфилда лежит следующая идея — запишем систему дифференциальных уравнений для градиентной минимизации «энергии» H (функции Ляпунова). Точки равновесия такой системы находятся в точках минимума энергии. Функцию энергии будем строить из следующих соображений:

1. Каждый эталон должен быть точкой минимума.

2. В точке минимума все координаты образа должны иметь значения ±1.

Функция

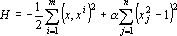
не удовлетворяет этим требованиям строго, но можно предполагать, что первое слагаемое обеспечит притяжение к эталонам (для вектора x фиксированной длины максимум квадрата скалярного произведения (x, xⁱ)? достигается при x= xⁱ…), а второе слагаемое

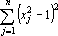
Используя выражение для энергии, можно записать систему уравнений, описывающих функционирование сети Хопфилда [312]:

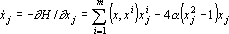
Сеть Хопфилда в виде (1) является сетью с непрерывным временем. Это, быть может, и удобно для некоторых вариантов аналоговой реализации, но для цифровых компьютеров лучше воспользоваться сетями, функционирующими в дискретном времени — шаг за шагом.

Построим сеть Хопфилда [312] с дискретным временем. Сеть должна осуществлять преобразование входного вектора x так, чтобы выходной вектор x' был ближе к тому эталону, который является правильным ответом. Преобразование сети будем искать в следующем виде:

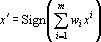
где w_i — вес i-го эталона, характеризующий его близость к вектору x, Sign — нелинейный оператор, переводящий вектор с координатами yi в вектор с координатами sign(yi).

Оглавление книги