Книга: Написание скриптов для Blender 2.49

Полет искр

Искры и все яркие эффекты подобного рода легко можно создать добавлением подходящей системы частиц к объекту. Множеством параметров систем частиц можно управлять с помощью весов в группе вершин, включая локальную плотность испускаемых частиц.

В этом примере мы хотели бы имитировать поведение электрического феномена, называемого "Огни святого Эльма". Это такой эффект, когда при определенных обстоятельствах, особенно в начале грозы, некоторые объекты начинают светиться. Это свечение называется  коронный   разряд (см.,   например, http://ru.wikipedia.org/wiki/Огни_святого_Эльма), и наиболее заметно на острых и выступающих частях более крупных структур, например, на радиоантеннах или громоотводах, где электрическое поле, которое вызывает этот эффект, наиболее сильное.

Для того, чтобы правдоподобно влиять на количество частиц, испускаемых мешем, нам нужно вычислять величину, называемую локальная кривизна, и хранить эту кривизну, нужным образом отмасштабированную, как вес в группе вершин. Затем, мы можем применить эту группу вершин к параметру плотности на дополнительной панели контекста частиц, чтобы управлять эмиссией.

Меш может иметь любую форму, и в большинстве случаев нет хорошей формулы, которая бы аппроксимировала его форму. Следовательно, мы аппроксимируем локальную кривизну неизбежно грубым способом (если нужна дополнительная информация и немного   тяжелой   математики,   смотрите http://en.wikipedia.org/wiki/Mean_curvature),   вычисляя   среднюю рёберную кривизну всех связанных с вершиной рёбер для каждой вершины в меше. Здесь мы определяем рёберную кривизну как скалярное произведение нормализованной вершинной нормали и вектора ребра (то есть, вектор, формируемый от вершины к её соседке). Это произведение будет отрицательным, если ребро изгибается вниз относительно нормали, и положительным, если оно изгибается вверх. Мы обратим этот знак, так как нам более привычно понятие положительной кривизны для пиков, а не для впадин. По-другому можно посмотреть на это так: в областях положительной кривизны угол между вершинной нормалью и ребром, начинающемся в той же вершине, больше 90°.

Следующий рисунок иллюстрирует концепцию - он изображает серию вершин, связанных рёбрами. У каждой вершины показана связанная с ней вершинная нормаль (стрелками). Вершины, обозначенные как a, имеют положительную кривизну, те, что обозначены b - отрицательную кривизну. Две из показанных вершин помечены буквой c, они находятся в области нулевой кривизны - в этих местах поверхность плоская, и вершинная нормаль перпендикулярна рёбрам.

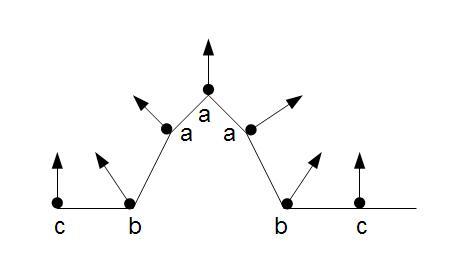
Расчет локальной кривизны

Функцию, которая вычисляет локальную кривизну для каждой вершины в меше, и возвращает список нормализованных весов, можно осуществить следующим образом:

from collections import defaultdict
def localcurvature(me,positive=False):
   end=defaultdict(list)
   for e in me.edges:
      end[e.v1.index].append(e.v2)
      end[e.v2.index].append(e.v1)
   weights=[]
   for v1 in me.verts:
      dvdn = []
      for v2 in end[v1.index]:
         dv = v1.co-v2.co
         dvdn.append(dv.dot(v1.no.normalize()))
      weights.append((v1.index,sum(dvdn)/max(len(dvdn),
                      1.0)))
   if positive:
      weights = [(v,max(0.0,w)) for v,w in weights]
   minimum = min(w for v,w in weights)
   maximum = max(w for v,w in weights)
   span = maximum - minimum
   if span > 1e-9:
      return [(v,(w-minimum)/span) for v,w in weights]
   return weights

Функция localcurvature() принимает меш и один опциональный аргумент, и возвращает список кортежей с индексом вершины и её весом. Если дополнительный аргумент - Истина, любой рассчитанный отрицательный вес отвергается.

Сложная работа выполняется на выделенных строках. Здесь мы проходим циклом над всеми вершинами, и затем, во внутреннем цикле, проверяем каждое связанное с текущей вершиной ребро, чтобы извлечь вершину на другом конце из предварительно рассчитанного словаря. Затем мы вычисляем dv как рёберный вектор и добавляем скалярное произведение этого рёберного вектора и нормализованной вершинной нормали в список dvdn.

weights.append((v1.index,sum(dvdn)/max(len(dvdn),1.0)))

Предшествующая строка может выглядеть странно, но она добавляет кортеж, состоящий из индекса вершины и средней кривизны, где среднее число получается вычислением суммы всех величин кривизны по каждому ребру из списка, и деления её на количество величин в списке. Поскольку список может быть пустым (это случается, когда меш содержит не связанные вершины), мы предохраняемся от ошибки деления на 0, деля её на длину списка или на единицу, в зависимости от того, что больше. Таким образом, мы сохраняем наш код более удобочитаемый, избегая оператора if.

Схема кода: curvature.py

С функцией localcurvature() в нашем расположении, сам скрипт вычисления кривизны становится совсем кратким (полный скрипт доступен как curvature.py):

if __name__ == "__main__":
   try:
      choice = Blender.Draw.PupMenu("Normalization%t|Only
                                     positive|Full range")
      if choice>0:
         ob = Blender.Scene.GetCurrent().objects.active
         me = ob.getData(mesh=True)
         try:
            me.removeVertGroup('Curvature')
         except AttributeError:
            pass
         me.addVertGroup('Curvature')
         for v,w in localcurvature(me,
                             positive=(choice==1)):
            me.assignVertsToGroup('Curvature',[v],w,
                             Blender.Mesh.AssignModes.ADD)
         Blender.Window.Redraw()
   except Exception as e:
      Blender.Draw.PupMenu('Error%t|'+str(e)[:80])

Выделенные строки показывают, что мы удаляем возможно существующую группу вершин Curvature из Меш-объекта внутри блока try, и отлавливаем исключение AttributeError, которое будет вызвано, если группа отсутствует. Затем, мы снова добавляем группу с тем же именем, так что она будет полностью пустая. Последняя выделенная строка показывает, как мы добавляем отдельно каждую вершину, поскольку любая вершина может иметь отличающийся от других вес.

Все действия окружены конструкцией  try … except , которая поймает любые исключения, и они появятся во всплывающем информационном сообщении, если произойдёт что-то необычное. Наиболее вероятно, это будет в ситуациях, когда пользователь забудет выбрать Меш-объект.

Собираем всё это вместе: Огни святого Эльма

Иллюстрация испускания из заострённого стержня была сделана моделированием простого объекта стержня вручную, и, затем, вычислением кривизны с помощью curvature.py.

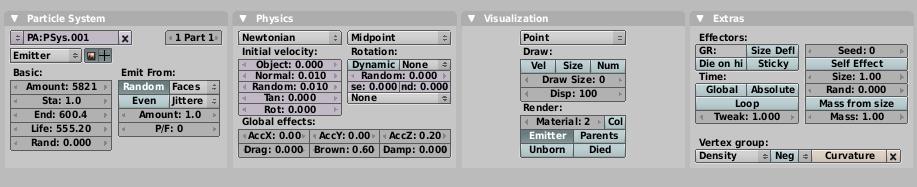
Затем, была добавлена система частиц и параметр плотности (density) в панели Extra был настроен на группу вершин Curvature. Стержню и системе частиц были даны отдельные материалы: простой серый и белое Хало соответственно. Частицы были симулированы для 250 кадров, и для иллюстрации представлен кадр 250.

Оглавление книги