Книга: Написание скриптов для Blender 2.49
Гравировка
Гравировка
Рассмотрим следующую проблему: дан некоторый текст, мы хотим отрендерить этот текст в виде утопленных бороздок на поверхности, подобно тому, как если бы они были выгравированы. Это не так уж просто, как кажется. Конечно, достаточно просто создать текстовый объект, но для того, чтобы манипулировать этим текстом, мы хотели бы преобразовать этот текстовый объект в меш. Интерфейс Блендера предлагает эту возможность в меню объектов, но как ни странно, API Блендера не предоставляет эквиалентной функции. Так, нашим первым барьером будет преобразование текстового объекта в меш.
Вторая проблема, которую мы должны решить - как выдавить набор вершин или рёбер на нужную глубину от поверхности. Опять же, в API Блендера нет функции для этого, так что мы должны добавить её к нашему пакету инструментов сами.
Последняя проблема более тонкая. Если нам каким-нибудь образом удалось создать несколько утопленных канавок, мы могли бы захотеть сделать краями чуть менее острыми, так как в действительности ничто не имеет абсолютно острых краёв. Существуют различные способы добиться этого, но многие из них включают добавление модификатора в наш меш. Модификатора скоса bevel может быть достаточно, чтобы убрать только острые края, но вполне вероятно, мы хотели бы добавить модификатор subsurface к нашему мешу целиком. Здесь у нас есть проблема: при заполнении промежутков между символами нашего текста, весьма вероятно, что мы столкнёмся со множеством узких треугольников. Эти треугольники испортят внешний вид результата нашего модификатора subsurface, как можно увидеть на следующем рисунке:

Две вещи могли бы помочь смягчить эту проблему. Одна - это добавить вес crease (складки) к рёбрам нашего выгравированного текста, этим самым взвешивая эти края сильнее, чем при расчете subsurface по умолчанию. Это может помочь, но может также отодвинуть нас от цели применения модификатора, так как это сделает эти края острыми. Следующий рисунок показывает результат: лучше, но все еще не выглядит идеально.

Другим подходом будет добавить дополнительный рёберный цикл ровно за пределами выгравированного текста. Это добавит кольцо четырёхугольных граней вокруг текста, заставляя subsurface вокруг текста вести себя намного лучше, как это можно увидеть ниже. В нашей конечной реализации мы применяем оба решения, но сначала мы примемся за каждую задачу поочередно.

Конвертация объекта Text3d в меш
Объект Text3d базируется на кривой с несколькими дополнительными параметрами. Блок данных, на который он ссылается - объект Кривой Блендера (Curve), и как только мы узнаем, как получить доступ к индивидуальным частям кривой, которые составляют каждый символ в нашем тексте, мы можем преобразовать эти кривые в вершины и рёбра. Все соответствующие функциональные возможности могут быть найдены в модулях Blender.Curve и Blender.Geometry.

txt = ob.getData()
curve = Blender.Curve.Get(txt.getName())
Теперь мы можем использовать txt, чтобы иметь доступ к Text3d-специфичной информации (например, txt.setText('foo')) и curve, чтобы иметь доступ к Curve-специфичной информации (например, curve.getNumCurves()).
Объект Curve Блендера состоят из множества объектов CurNurb, которые представляют сегменты кривой. Единственный текстовый символ обычно состоит из одного или двух сегментов кривой. Маленькая буква e, например, состоит из внешнего сегмента и небольшого внутреннего сегмента кривой. Объекты CurNurb, в свою очередь, состоят из множества узлов или управляющих точек, которые задают сегмент кривой. В случае объектов Text3d эти узлы всегда являются объектами BezTriple, и модуль Geometry Блендера предоставляет нам функцию BezierInterp(), которая возвращает список координат, интерполированных между двумя точками. Эти точки и направляющие кривой в этих точках (часто называемые handle, рукоять), можно взять из объектов BezTriple. Результирующий код выглядит так (полный код является частью нашего пакета разработчика в Tools.py) (Эта и последующие функции этого раздела, несмотря на заверения автора, отсутствуют в файле Tools.py, прилагаемом ко 2-й главе, найти их можно только в файле engrave.py — прим. пер.):
import Blender
from Blender.Geometry import BezierInterp as interpolate
from Blender.Mathutils import Vector as vec
def curve2mesh(c):
vlists=[]
for cn in c:
npoints = len(cn)
points=[]
first=True
for segment in range(npoints-1):
a=cn[segment].vec
b=cn[segment+1].vec
lastpoints = interpolate(vec(a[1]),vec(a[2]),
vec(b[0]), vec(b[1]),6)
if first:
first = False
points.append(lastpoints[0])
points.extend(lastpoints[1:])
if cn.isCyclic():
a=cn[-1].vec
b=cn[0].vec
lastpoints=interpolate(vec(a[1]), vec(a[2]),
vec(b[0]), vec(b[1]),6)
points.extend(lastpoints[:-2])
vlists.append(points)
return vlists
Выделенные строки показывают два важных аспекта. Первая показывает фактическую интерполяцию. Мы переименовали довольно неуклюжее имя функции BezierInterp() в interpolate(), и она принимает пять аргументов. Первые четыре берутся от двух объектов BezTriple, между которыми мы интерполируем. В каждом объекте BezTriple можно получить доступ к списку из трех векторов: входящая рукоять, позиция точки, и исходящая рукоять (смотри следующий рисунок). Мы передаем позицию первой точки и исходящей рукояти и позицию второй точки и входящей рукояти. Пятый аргумент является количеством точек, которые мы хотим получить на выходе функции interpolate().
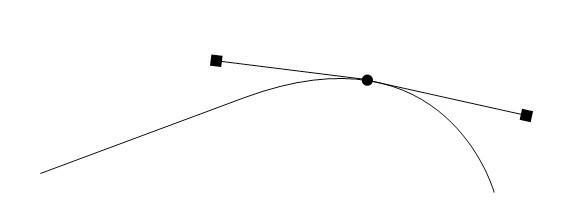
Вторая выделенная строка заботится о замкнутых кривых - кривых, в которых их первые и последние точки связаны. Это является случаем всех кривых, которые формируют символы в тексте. Функция возвращает список списков. Каждый список содержит все интерполированные точки (кортежи из x, y, z координат) для каждой кривой. Заметьте, что некоторые символы состоят из более, чем одной кривой. Например, небольшая буква e во многих шрифтах, или буква o состоит из двух кривых, одна задаёт внешнюю границу буквы и одна внутреннюю. Объект Text3d, содержащий текст Foo, например, возвращает список из пяти списков - первый будет содержать вершины, определяющие большую букву F, а второй и третий будут содержать вершины для двух кривых, которые создают маленькую букву o, так же будет с четвертым и пятым.
Выдавливание рёберного цикла
Выдавливание (Extrusion) является процессом, где мы дублируем вершины (и, возможно, соединяющие их рёбра) и перемещаем их в некотором направлении, после чего мы соединяем эти дубликаты вершин с их оригиналами новыми рёбрами, и заканчиваем операцию, создавая новую грань между старыми и новыми вершинами. Нам нужно это для того, чтобы утопить очертание нашего текста, чтобы создать бороздку с вертикальными стенками. Функция extrude_selected_edges() в Tools.py принимает меш и вектор как аргументы, и выдавит вершины на выбранных рёбрах в меше в направлении вектора, добавляя все необходимые новые рёбра и грани. Поскольку эта техника является расширением того, что мы уже видели раньше, код не показан здесь.
Расширение (Expanding) рёберного цикла
Если у нас есть список рёбер, формирующих замкнутую кривую (или более одного), определяющий символ, мы хотели бы окружить эти рёбра дополнительным рёберным циклом, чтобы создать лучшее "выполнение" любого модификатора subsurface, который конечный пользователь может связать с нашим мешем. Это был бы довольно сложный процесс, если мы должны были бы вычислять это в 3D, но, к счастью, наши преобразованные символы имеют все свои вершины на плоскости xy (дело в том, что все символы в новых экземплярах Text3d объекта лежат на плоскости xy)..
Всего лишь два измерения - это вполне податливая проблема. Для каждой точки в нашем рёберном цикле мы определяем направление вершинной нормали. Вершинная нормаль является линией, разрезающей пополам угол между двумя рёбрами, которые делят рассматриваемую нами точку. Если два ребра коллинеарны (или почти так), мы берем за вершинную нормаль линию, перпендикулярную одному из рёбер. Позиция точки, создаваемой в новом рёберном цикле, будет где-нибудь на этой нормали. Для того, чтобы определиться, должны ли мы перемещать наружу или внутрь вдоль этой нормали, мы просто пробуем одно направление и проверяем новую позицию - находится ли она внутри границ нашего символа. Если это так, мы берём обратное направление.
Один вопрос по-прежнему нуждается в решении: символ может состоять из более, чем одной кривой. Если мы хотим сделать дополнительные рёберные циклы вокруг такого символа, такой рёберный цикл должен быть снаружи внешней границы символа, но внутри любой внутренней кривой. Другими словами, если мы создаем новый рёберный цикл, мы должны знать, лежит ли кривая внутри другой кривой. Если это так, то она не является внешней границей, и новый рёберный цикл должен быть создан лежащим внутри кривой. Следовательно, наша функция expand() (показанная в следующем куске кода, полный код является частью Tools.py. На самом деле эта и все вызываемые ею функции находятся в файле expand.py — прим. пер.), берет дополнительный опциональный аргумент plist, который является списком списков, содержащих объекты MVert, определяющие дополнительные полигоны, чтобы сверяться с ними. Если первая точка кривой, которую мы хотим расширить, лежит в пределах любой из этих дополнительных кривых, мы принимаем, что кривая, которую мы расширяем, является внутренней кривой. (Это будет неверным предположением, если внутренняя кривая будет пересекать внешнюю кривую в некоторой точке, но для кривых, определяющих символ в шрифте, такого никогда не происходит.)
def expand(me,loop,offset=0.05,plist=[]):
ov = [me.verts[i] for i in verts_from_edgeloop(loop)]
inside=False
for polygon in plist:
if in_polygon(loop[0].v1.co,polygon):
inside=True
break # мы не имеем дел с несколькими
включениями
n=len(ov)
points=[]
for i in range(n):
va = (ov[i].co-ov[(i+1)%n].co).normalize()
vb = (ov[i].co-ov[(i-1)%n].co).normalize()
cosa=abs(vec(va).dot(vb))
if cosa>0.99999 : # почти коллинеарны
c = vec(va[1],va[0],va[2])
else:
c = va+vb
l = offset/c.length
p = ov[i].co+l*c
if in_polygon(p,ov) != inside:
p = ov[i].co-l*c
print i,ov[i].co,va,vb,c,l,cosa,p
points.append(p)
return points
Выделенный код вызывает функцию (приведенную в Tools.py), которая принимает список рёбер, формирующих рёберный цикл, и возвращает отсортированный список вершин. Это необходимо, поскольку наша функция in_polygon() принимает список вершин, а не рёбер, и предполагает, что этот список отсортирован, то есть смежные вершины формируют рёбра, которые не пересекаются.
Чтобы определить, находится ли точка внутри замкнутого многоугольника, определяемого списком вершин, мы считаем количество рёбер, которые пересекаются линией (часто называемой лучом), которая начинается в данной точке и распространяется до бесконечности. Если количество пересекаемых рёбер нечетное, точка лежит внутри многоугольника; если четное, она лежит снаружи многоугольника. Следующий рисунок иллюстрирует концепцию:
Функция in_polygon(), показанная здесь - часть Tools.py. Она принимает точку (Вектор) и список вершин (объекты MVert) и возвращает или Истину или Ложь. Заметьте, что любая z-координата у точки или у вершины в многоугольнике игнорируются.
from Blender.Geometry import LineIntersect2D
from Blender.Mathutils import Vector as vec
def in_polygon(p,polygon):
intersections = 0
n = len(polygon)
if n<3 : return False
for i in range(n):
if LineIntersect2D (p,vec(1.0,0.0,0.0),polygon[i].
co,polygon[(i+1)%n].co):
intersections+=1
return intersections % 2 == 1
Трудная задача выполняется на выделенной строке функцией LineIntersect2D(), доступной в модуле Blender.Geometry. Действие деление по модулю (%) в операторе return - способ определить, нечетное ли количество пересечений.
Собираем всё вместе: Engrave.py
Вооруженные всеми вспомогательными функциями, разработанными в предыдущих секциях, мы можем сделать список шагов, которые мы должны предпринять для того, чтобы выгравировать текст:
1. Показать всплывающее меню для ввода строки, которую надо гравировать.
2. Проверить, что активный объект - меш, и выбраны грани.
3. Создать объект Text3d.
(на самом деле скрипт engrave.py требует, чтобы объект Text3d уже был создан и выбран как активный, так что первые 3 пункта не полностью соответствуют действительности — прим. пер.)
4. Преобразовать его в меш, с подходящими группами вершин.
5. Добавить дополнительные рёберные циклы к символам.
6. Выдавить оригинальные символы вниз.
7. Заполнить низ выдавленных символов.
8. Добавить "cartouche" (прямоугольник) вокруг текста.
9. Заполнить пространство между cartouche и символами.
10.Добавить модификатор subsurface.
11.Установить величину crease (складки) на рёбрах, содержащихся в группах вершин TextTop и TextBottom.
Наш окончательный скрипт следует за этой схемой почти в точности и использует инструменты, которые мы разработали раньше в этой главе. Мы покажем здесь наиболее важные секции (полный скрипт доступен как engrave.py). Мы начинаем с преобразования объекта Text3d (c в следующем коде) в список, содержащий список позиций вершин для каждого сегмента кривой в тексте, и мы добавляем новый пустой Меш-объект в сцену с несколькими пустыми группами вершин:
vlist = curve2mesh(c)
me = Blender.Mesh.New('Mesh')
ob = Blender.Scene.GetCurrent().objects.new(me,'Mesh')
me.addVertGroup('TextTop')
me.addVertGroup('TextBottom')
me.addVertGroup('Outline')
Следующий шаг должен добавить эти вершины в меш и создать соединяющие рёбра. Так как все сегменты кривой в символе замкнуты, мы должны позаботиться о добавлении дополнительного ребра, чтобы соединить мостом промежуток между последней и первой вершиной, как показано на выделенной строке. На всякий случай, мы удаляем любые задвоения, которые могут присутствовать в интерполированном сегменте кривой. Мы добавляем вершины к группе вершин TextTop и сохраняем ссылку на список новых рёбер для будущего использования.
loop=[]
for v in vlist:
offset=len(me.verts)
me.verts.extend(v)
edgeoffset=len(me.edges)
me.edges.extend([(i+offset,i+offset+1)
for i in range(len(v)-1)])
me.edges.extend([(len(v)-1+offset,offset)])
me.remDoubles(0.001)
me.assignVertsToGroup('TextTop',
range(offset,len(me.verts)),
1.0,
Blender.Mesh.AssignModes.ADD)
loop.append([me.edges[i] for i in range(edgeoffset,
len(me.edges) )])
Для каждого рёберного цикла, который мы сохранили в предыдущей части, мы создаем новый, и немного больший, рёберный цикл вокруг него и добавляем эти новые вершины и рёбра к нашему мешу. Мы также хотим создать грани между этими рёберными циклами, и это действие начинается на выделенной строке: здесь мы используем встроенную функцию Питона zip(), чтобы получить пары рёбер двух рёберных циклов. Каждый рёберный цикл упорядочен вспомогательной функцией (доступной в Tools.py), которая сортирует рёбра, чтобы они лежали в порядке, в котором они соединены друг с другом. Для каждой пары рёбер мы создаем две возможных организации индексов вершин и вычисляем, какая из них формирует нескрученную грань. Это вычисление производится посредством функции least_warped() (код не показан), которая основана на сравнении периметров граней, заданных двумя различными порядками вершин. Нескрученная грань будет иметь самый короткий периметр, именно её мы затем добавляем к мешу.
for l in range(len(loop)):
points = expand.expand(me,loop[l],
0.02,loop[:l]+loop[l+1:])
offset=len(me.verts)
me.verts.extend(points)
edgeoffset=len(me.edges)
me.edges.extend([(i+offset,i+offset+1)
for i in range(len(points)-1)])
me.edges.extend([(len(points)-1+offset,offset)])
eloop=[me.edges[i] for i in
range(edgeoffset,len(me.edges))]
me.assignVertsToGroup('Outline',
range(offset,len(me.verts)),
1.0,
Blender.Mesh.AssignModes.ADD)
faces=[]
for e1,e2 in zip( expand.ordered_edgeloop(loop[l]),
expand.ordered_edgeloop(eloop)):
f1=(e1.v1.index,e1.v2.index,
e2.v2.index,e2.v1.index)
f2=(e1.v2.index,e1.v1.index,
e2.v2.index,e2.v1.index)
faces.append(least_warped(me,f1,f2))
me.faces.extend(faces)
Мы опустили код выдавливания рёберной петли символа, но следующие строки содержательны, так как они показывают, как заполняется рёберный цикл. Сначала мы выбираем все важные рёбра, используя две вспомогательные функции (это - выдавленные рёбра символов). Затем, мы вызываем метод fill(). Этот метод будет заполнять любой набор замкнутых рёберных циклов до тех пор, пока они лежат в одной плоскости. Он даже позаботится об отверстиях (подобно небольшому острову в букве e):
deselect_all_edges(me)
select_edges(me,'TextBottom')
me.fill()
Дополнение cartouche - просто вопрос добавления прямоугольного рёберного цикла вокруг наших символов. Если этот рёберный цикл выбрать вместе с вершинами в группе вершин Outline, можно снова использовать метод fill() для заполнения этого cartouche. Это не показано здесь. Несколько заключительных штрихов: мы по возможности преобразуем треугольники в нашем меше в четырехугольники, используя метод triangleToQuad(), затем подразделяем меш. Мы также добавляем модификатор subsurface, устанавливаем атрибут сглаживания (smooth) на всех гранях и пересчитываем нормали всех граней, чтобы они согласованно указывали наружу.
me.triangleToQuad()
me.subdivide()
mod = ob.modifiers.append(
Blender.Modifier.Types.SUBSURF)
mod[Blender.Modifier.Settings.LEVELS]=2
select_all_faces(me)
set_smooth(me)
select_all_edges(me)
me.recalcNormals()

Мы видели, что модификаторы, доступные в Блендере, можно добавлять к объекту в Питоне. Есть, тем не менее, один модификатор, который может быть добавлен, но создаётся впечатление, что он не имеет эквивалента в графическом интерфейсе Блендера. Это - так называемый модификатор Hook (Захват). Захват в Блендере - способ сделать родителем вершин объект (так что это противоположно vertex parenting, где мы родителем объекта назначаем вершины), и в приложении самостоятельно может быть доступно через меню Mesh | Vertex | Add Hook в режиме редактирования. После добавления он появится в списке модификаторов. С точки зрения программиста, модификатор Захвата никак не отличается из других модификаторов, но увы, ни его тип, ни параметры, не документированы в API.
Добавление переводчика к разделу Гравировка:
К сожалению, опробованная мной программа engrave.py (с необходимым ей модулем expand.py), скачанная с сайта издательства, работала далеко не так красиво, как это описано в тексте. В очередной раз придётся набраться наглости и указать на недоработки автора.
1. Простая ошибка в программе: ближе к концу есть такие строки:
me.subdivide()
me.triangleToQuad()
me.subdivide()
перед преобразованием в четырёхугольники, и тем более, перед подразделением необходимо было выделить все вершины, а к этому моменту они выделены все, кроме основного контура букв. В результате, меш подразделяется на устрашающее количество лишних треугольников. Я заменил первое подразделение на выбор всех рёбер.
select_all_edges(me)
me.triangleToQuad()
me.subdivide()
2. Расширение или окантовка некоторых символов происходила внутрь, а не наружу, как положено, т.е. проверка на то, является ли контур внутренним, не всегда срабатывала правильно. На мой взгляд, проблема состоит в этой строке функции in_polygon() модуля expand:
if cross(p,vec(1.0,0.0,0.0),polygon[i].co,
polygon[(i+1)%n].co):
Насколько я понял, второй конец проверяемого луча vec(1.0,0.0,0.0) взят произвольно, и это вызывает накладки в отдельных случаях. Для себя я просто поставил более удалённый вектор vec(1000.0,0.0,0.0), и программа в моём тестовом случае перестала ошибаться. В общем же случае программа должна сама по некоторому алгоритму вычислять этот вектор так, чтобы наверняка исключить возможность ошибок.
3. Самое страшное: заполнение пространства между буквами выполняется пресловутой функцией fill() (её аналог в интерфейсе Блендера - Shift-F), результатом которой и являются множество треугольников с очень острыми углами. С тем же успехом можно было сразу применить булеановское вычитание и не мучиться. Возможно, добавлением специальной функции красивого заполнения проблему можно решить, но, думаю, такая функция вряд-ли будет простой.




