Книга: Рассказы о математике с примерами на языках Python и C
Парадокс дней рождений
Парадокс дней рождений
Допустим, в организации работает 24 человека. Какова вероятность что хотя бы двое отмечают день рождения в один и тот же день? Интуитивно кажется, что эта вероятность весьма мала и будет равна 24/365, но и в этом случае интуиция ошибается. В реальности, мы должны рассматривать количествопар, которые могут образовать данные люди. Это число довольно-таки велико, например, если обозначить 5 человек как ABCDE, то количество возможных пар будет 10 (AB, AC, AD, AE, BC, BD, BE, CD, CE, DE), а для группы из 24 человек возможно 276 пар.
Для точного расчета воспользуемся принципом произведения вероятностей. Вероятность того, что для 2х людей день рождения не совпадет, равна 364/365. Для 3х человек вероятность что все дни не совпадут, равна произведению 364/365 * 363/365, и так далее. Для n-человек формула приведена в Википедии:
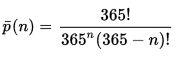
(n! — обозначение факториала, n! = 1 * 2* .. * (n - 1) * n)
Нужная нам вероятность обратного события равна обратной величине:
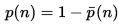
Вывести все значения несложно с помощью программы на Python:
import math
def C(n):
return 1000 – 1000 * math.factorial(365) / (math.factorial(365 – n) * 365**n)
for n in range(3, 50):
print("{} - {}%").format(n, 0.1 * C(n))
365! это очень большое число, поэтому здесь использованы целочисленные вычисления языка Python, уже затем значение было переведено в проценты.
В результате получаем следующую таблицу:
| 3 | 0.0082 | 4 | 0.0163 | 5 | 0.0271 |
| 6 | 0.0404 | 7 | 0.0562 | 8 | 0.0743 |
| 9 | 0.0946 | 10 | 0.1169 | 11 | 0.1411 |
| 12 | 0.1670 | 13 | 0.1944 | 14 | 0.2231 |
| 15 | 0.2529 | 16 | 0.2836 | 17 | 0.3150 |
| 18 | 0.3469 | 19 | 0.3791 | 20 | 0.4114 |
| 21 | 0.4436 | 22 | 0.4756 | 23 | 0.5072 |
| 24 | 0.5383 | 25 | 0.5686 | 26 | 0.5982 |
| 27 | 0.6268 | 28 | 0.6544 | 29 | 0.6809 |
| 30 | 0.7063 | 31 | 0.7304 | 32 | 0.7533 |
| 33 | 0.7749 | 34 | 0.7953 | 35 | 0.8143 |
| 36 | 0.8321 | 37 | 0.8487 | 38 | 0.8640 |
| 39 | 0.8782 | 40 | 0.8912 | 41 | 0.9031 |
| 42 | 0.9140 | 43 | 0.9239 | 44 | 0.9328 |
| 45 | 0.9409 | 46 | 0.9482 | 47 | 0.9547 |
| 48 | 0.9605 | 49 | 0.9657 | 50 | 0.9703 |
Как видно из таблицы, уже при количестве сотрудников 50 человек, хотя бы 1 день рождения почти гарантированно совпадет (вероятность 97%), а для 24 человек получаем вероятность равную 0.538, т. е. более 50%.
- 12. Парадоксы теории вероятности
- Парадокс Монти Холла
- Парадокс расширения-специализации
- Глава 5 Как самостоятельно внедрить CRM-систему за 50 дней (7 этапов)
- Глава 1 От отца-домохозяйки до шестизначного дохода за семь дней
- Предисловие Домены древности и наших дней
- Как родилась идея плана «90 дней»
- Приложение 1. Заповеди плана «90 дней»
- Часть IV. Стиль парадоксального управления Samsung и будущее концепции «Путь Samsung»
- Как отчитаться по плану «90 дней»
- АГС, горе от ума и парадоксы современного SEO
- Парадоксальный креатив прямой рекламы




