Книга: Рассказы о математике с примерами на языках Python и C

9. Числа Фибоначчи

9. Числа Фибоначчи

Возьмем 2 числа: 0 и 1. Следующее число рассчитаем как сумму предыдущих чисел, затем повторим процесс.

Мы получили последовательность, известную как числа Фибоначчи:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ...

Эта последовательность была названа в честь итальянского математика 12 века Леонардо Фибоначчи. Фибоначчи рассматривал задачу роста популяции кроликов. Если предположить, что новорожденная пара кроликов 1 месяц растет, через месяц начинает спариваться, и затем через каждый месяц дает потомство, то количество пар кроликов несложно подсчитать:

Как можно видеть, число пар образует как раз те самые числа Фибоначчи. Сама последовательность Фибоначчи кажется простой. Но чем она интересна? Пример с кроликами не случаен — эти числа действительно описывают множество природных закономерностей:

? Множество растений имеют количество лепестков, равное одному из чисел Фибоначчи. Количество листьев на стебле также может описываться этим законом, например у тысячелистника.

? Другое известное изображение — спираль Фибоначчи, которая строится по похожему принципу соотношения размеров прямоугольников:

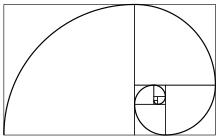
Это изображение также часто встречается в природе, от раковин моллюсков, до формы атмосферного циклона или даже спиральной галактики.

Для примера достаточно взять фотографию циклона из космоса, и наложить обе картинки вместе:

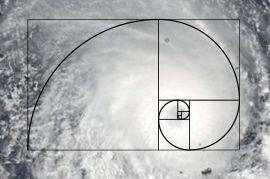
? Если взять и разделить друг на друга 2 любых соседних члена последовательности, например 233/377, получится число 0,618. Случайно это или нет, но это число — то самое «золотое сечение», считающееся наиболее эстетичной пропорцией.

Числа Фибоначчи несложно вывести в программе на языке Python:

from decimal import *
def printNumbers(n):
    i1 = Decimal(0)
    i2 = Decimal(1)
    for p in range(1, n+1):
        print("F({}) = {}".format(p, i2))
        fib = i1 + i2
        i1 = i2
        i2 = fib
getcontext().prec = 100
N = 100
printNumbers(N)

Интересно заметить, что растет последовательность Фибоначчи весьма быстро, уже

F(300) = 222232244629420445529739893461909967206666939096499764990979600.

Оглавление книги