Книга: Учебное пособие по курсу «Нейроинформатика»

Контрастирование без ухудшения

Контрастирование без ухудшения

Пусть нам дана только обученная нейронная сеть и обучающее множество. Допустим, что вид функции оценки и процедура обучения нейронной сети неизвестны. В этом случае так же возможно контрастирование сети. Предположим, что данная сеть идеально решает задачу. В этом случае возможно контрастирование сети даже при отсутствии обучающей выборки, поскольку ее можно сгенерировать используя сеть для получения ответов. Задача не ухудшающего контрастирования ставится следующим образом: необходимо так провести контрастирование параметров, чтобы выходные сигналы сети при решении всех примеров изменились не более чем на заданную величину. Для решения задача редуцируется на отдельный адаптивный сумматор: необходимо так изменить параметры, чтобы выходной сигнал адаптивного сумматора при решении каждого примера изменился не более чем на заданную величину.

Обозначим через x^qpp-й входной сигнал сумматора при решении q-о примера; через f^q — выходной сигнал сумматора при решении q-о примера; через wp— вес p-о входного сигнала сумматора; через ? — требуемую точность; через n — число входных сигналов сумматора; через m — число примеров. Очевидно, что при решении примера выполняется равенство

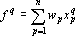
Требуется найти такой набор индексов I={i₁,…,i_k}, что

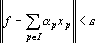
где ?p— новый вес p-о входного сигнала сумматора. Набор индексов будем строить по следующему алгоритму.

1. Положим f⁽⁰⁾=f, x^•p=xp, I⁽⁰⁾=?, J⁽⁰⁾={1,…,n}, k =0.

2. Для всех векторов x^•pтаких, что p?J^(k), проделаем следующее преобразование: если

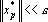
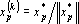
3. Если

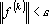
4. Находим i_k+1 — номер вектора, наиболее близкого к f^(k) из условия

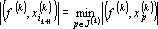
5. Исключаем i_k+1 из множества индексов обрабатываемых векторов: J^(k+1)=J^(k)/{i_k+1}.

6. Добавляем i_k+1  в множество индексов найденных векторов: I^(k+1)=I^(k)?{i_k+1}.

7. Вычисляем не аппроксимированную часть (ошибку аппроксимации) вектора выходных сигналов:

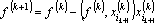
8. Преобразуем обрабатываемые вектора к промежуточному представлению — ортогонализуем их к вектору

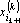
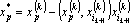
9. Увеличиваем k на единицу и переходим к шагу 2.

10. Если k=0, то весь сумматор удаляется из сети и работа алгоритма завершается.

11. Если k=n+1, то контрастирование невозможно и сумматор остается неизменным.

12. В противном случае полагаем I=I^(k) и вычисляем новые веса связей ?p(p?I) решая систему уравнений

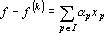
13. Удаляем из сети связи с номерами p?J, веса оставшихся связей полагаем равными ?p(p?I).

Данная процедура позволяет производить контрастирование адаптивных сумматоров. Причем значения, вычисляемые каждым сумматором после контрастирования, отличаются от исходных не более чем на заданную величину. Однако, исходно была задана только максимально допустимая погрешность работы сети в целом. Способы получения допустимых погрешностей для отдельных сумматоров исходя из заданной допустимой погрешности для всей сети описаны в ряде работ [95–97, 168, 210–214, 355].

Оглавление книги