Книга: Учебное пособие по курсу «Нейроинформатика»

Процедура контрастирования

Существует два типа процедуры контрастирования — контрастирование по значимости параметров и не ухудшающее контрастирование. В данном разделе описаны оба типа процедуры контрастирования.

Контрастирование на основе показателей значимости

С помощью этой процедуры можно контрастировать, как входные сигналы, так и параметры сети. Далее в данном разделе будем предполагать, что контрастируются параметры сети. При контрастировании входных сигналов процедура остается той же, но вместо показателей значимости параметров сети используются показатели значимости входных сигналов. Обозначим через ?p— показатель значимости p-о параметра; через w⁰p— текущее значение p-о параметра; через w^•p— ближайшее выделенное значение для p-о параметра.

Используя введенные обозначения процедуру контрастирования можно записать следующим образом:

1. Вычисляем показатели значимости.

2. Находим минимальный среди показателей значимости — ?_p'.

3. Заменим соответствующий этому показателю значимости параметр w⁰_p? на w^•_p?, и исключаем его из процедуры обучения.

4. Предъявим сети все примеры обучающего множества. Если сеть не допустила ни одной ошибки, то переходим ко второму шагу процедуры.

5. Пытаемся обучить полученную сеть. Если сеть обучилась безошибочному решению задачи, то переходим к первому шагу процедуры, в противном случае переходим к шестому шагу.

6. Восстанавливаем сеть в состояние до последнего выполнения третьего шага. Если в ходе выполнения шагов со второго по пятый был отконтрастирован хотя бы один параметр, (число обучаемых параметров изменилось), то переходим к первому шагу. Если ни один параметр не был отконтрастирован, то получена минимальная сеть.

Возможно использование различных обобщений этой процедуры. Например, контрастировать за один шаг процедуры не один параметр, а заданное пользователем число параметров. Наиболее радикальная процедура состоит в контрастировании половины параметров связей. Если контрастирование половины параметров не удается, то пытаемся контрастировать четверть и т. д. Другие варианты обобщения процедуры контрастирования будут описаны при описании решения задач. Результаты первых работ по контрастированию нейронных сетей с помощью описанной процедуры опубликованы в [47, 303, 304].

Контрастирование без ухудшения

Пусть нам дана только обученная нейронная сеть и обучающее множество. Допустим, что вид функции оценки и процедура обучения нейронной сети неизвестны. В этом случае так же возможно контрастирование сети. Предположим, что данная сеть идеально решает задачу. В этом случае возможно контрастирование сети даже при отсутствии обучающей выборки, поскольку ее можно сгенерировать используя сеть для получения ответов. Задача не ухудшающего контрастирования ставится следующим образом: необходимо так провести контрастирование параметров, чтобы выходные сигналы сети при решении всех примеров изменились не более чем на заданную величину. Для решения задача редуцируется на отдельный адаптивный сумматор: необходимо так изменить параметры, чтобы выходной сигнал адаптивного сумматора при решении каждого примера изменился не более чем на заданную величину.

Обозначим через x^qpp-й входной сигнал сумматора при решении q-о примера; через f^q — выходной сигнал сумматора при решении q-о примера; через wp— вес p-о входного сигнала сумматора; через ? — требуемую точность; через n — число входных сигналов сумматора; через m — число примеров. Очевидно, что при решении примера выполняется равенство

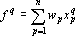
Требуется найти такой набор индексов I={i₁,…,i_k}, что

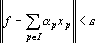
где ?p— новый вес p-о входного сигнала сумматора. Набор индексов будем строить по следующему алгоритму.

1. Положим f⁽⁰⁾=f, x^•p=xp, I⁽⁰⁾=?, J⁽⁰⁾={1,…,n}, k =0.

2. Для всех векторов x^•pтаких, что p?J^(k), проделаем следующее преобразование: если

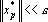
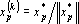
3. Если

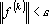
4. Находим i_k+1 — номер вектора, наиболее близкого к f^(k) из условия

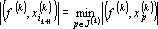
5. Исключаем i_k+1 из множества индексов обрабатываемых векторов: J^(k+1)=J^(k)/{i_k+1}.

6. Добавляем i_k+1  в множество индексов найденных векторов: I^(k+1)=I^(k)?{i_k+1}.

7. Вычисляем не аппроксимированную часть (ошибку аппроксимации) вектора выходных сигналов:

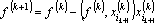
8. Преобразуем обрабатываемые вектора к промежуточному представлению — ортогонализуем их к вектору

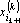
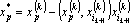
9. Увеличиваем k на единицу и переходим к шагу 2.

10. Если k=0, то весь сумматор удаляется из сети и работа алгоритма завершается.

11. Если k=n+1, то контрастирование невозможно и сумматор остается неизменным.

12. В противном случае полагаем I=I^(k) и вычисляем новые веса связей ?p(p?I) решая систему уравнений

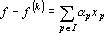
13. Удаляем из сети связи с номерами p?J, веса оставшихся связей полагаем равными ?p(p?I).

Данная процедура позволяет производить контрастирование адаптивных сумматоров. Причем значения, вычисляемые каждым сумматором после контрастирования, отличаются от исходных не более чем на заданную величину. Однако, исходно была задана только максимально допустимая погрешность работы сети в целом. Способы получения допустимых погрешностей для отдельных сумматоров исходя из заданной допустимой погрешности для всей сети описаны в ряде работ [95–97, 168, 210–214, 355].

Оглавление книги