Книга: JavaScript. Подробное руководство, 6-е издание

21.4.5. Рисование и заливка кривых

21.4.5. Рисование и заливка кривых

Контур - это последовательность фрагментов контура, а фрагмент контура - это последовательность точек, соединенных линиями. В контурах, которые определялись в разделе 21.4.1, эти точки соединялись прямыми линиями, но это не обязательно должно быть так. Объект CanvasRenderingContext2D определяет несколько методов, которые добавляют во фрагмент контура новую точку и соединяют ее кривой с текущей точкой:

агс()

Этот метод добавляет во фрагмент контура дугу. Он соединяет текущую точку с началом дуги прямой линией и затем соединяет начало дуги с концом дуги сегментом окружности, при этом конечная точка дуги становится новой текущей точкой. Дуга определяется шестью параметрами: координаты X и Y центра окружности, радиус окружности, угол начала и конца дуги и направление (по часовой стрелке или против часовой стрелки) рисования дуги между этими двумя углами.

агсТо()

Этот метод так же рисует прямую линию и круговую дугу, как и метод агс(), но при его использовании дуга определяется другим набором параметров. Аргументы метода агсТо() определяют точки Р1 и Р2 и радиус. Дуга, добавляемая в контур, имеет указанный радиус и строится так, что линии, соединяющие текущую точку с точкой Р1 и точку Р1 с точкой Р2, являются касательными к ней. Такой необычный, на первый взгляд, способ определения дуг в действительности является весьма удобным при рисовании закругленных углов. Если указать радиус равный 0, этот метод просто нарисует прямую линию, соединяющую текущую точку и точку Р1. Однако если указан ненулевой радиус, он нарисует прямую линию от текущей точки в направлении точки Р1 до начала дуги, затем начнет рисовать круговую дугу, пока направление рисования не совпадет с направлением на точку Р2.

bezierCurveTo()

Этот метод добавит во фрагмент контура новую точку Р и соединит ее с текущей точкой кубической кривой Безье. Форма кривой определяется двумя «контрольными точками» С1 и С2. В начале кривой (в текущей точке) рисование начинается в направлении точки С1. В свой конец (в точке Р) кривая приходит в направлении из точки С2. Между этими точками кривая плавно изгибается. Точка Р становится новой текущей точкой для фрагмента контура.

quadraticCurveTo()

Этот метод похож на метод bezierCurveTo(), но рисует квадратичные кривые Безье и имеет всего одну контрольную точку.

С помощью этих методов можно рисовать контуры, подобные тем, что изображены на рис. 21.9.

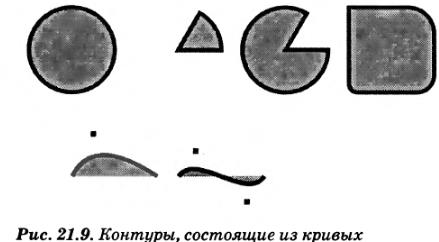
В примере 21.7 представлен программный код, с помощью которого было создано изображение на рис. 21.9. Методы, используемые в этом примере, являются одними из самых сложных в прикладном интерфейсе объекта Canvas. Полное описание методов и их аргументов приводится в справочном разделе книги.

Пример 21.7. Добавление кривых в контур

// Вспомогательная функция для преобразования градусов в радианы
function rads(x) { return Math.PI*x/180; }
// Нарисовать окружность. Используйте масштабирование и вращение, если требуется
// получить эллипс. Здесь не используется текущая точка, поэтому окружность рисуется
// без прямой линии, соединяющей текущую точку с началом окружности,
с.beginPath();
с.агс(75,100,50,          // Центр в точке (75,100), радиус 50
     0,rads(360),false);  // По часовой стрелке от 0 до 360 градусов
// Нарисовать сектор. Углы откладываются по часовой стрелке от положительной оси х.
// Обратите внимание, что метод агс() добавляет линию от текущей точки к началу дуги.
c.moveTo(200, 100);     // Перейти в центр окружности
с.агс(200, 100, 50,     // Центр окружности и радиус
    rads(-60), rads(0), // Начальный угол -60 градусов, конечный 0 градусов
            false);     // false означает по часовой стрелке
с.closePath();          // Добавить прямую линю к центру окружности
// Тот же сектор, в противоположном направлении
c.moveTo(325, 100);
с.агс(325, 100, 50, rads(-60), rads(0), true); // Против часовой стрелки
c.closePath();
// Использовать агсТо() для закругления углов. Здесь рисуется квадрат с верхним левым
// углом в точке (400,50), с закруглениями углов дугами с разными радиусами.
c.moveTo(450, 50);            // Середина верхней стороны,
с.агсТо(500,50,500,150,30);   // Насть верхней стороны и правый верхний угол,
с.агсТо(500,150,400,150,20);  // Добавить правую сторону и правый нижний угол,
с.агсТо(400,150,400,50,10);   // Добавить нижнюю сторону и левый нижний угол,
с.агсТо(400,50,500,50,0);     // Добавить левую сторону и левый верхний угол,
с.closePath(); // Замкнуть контур, чтобы добавить остаток верхней стороны.
// Квадратичная кривая Безье: одна контрольная точка
c.moveTo(75, 250);                     // Начало в точке (75,250)
с.quadraticCurveTo(100,200, 175, 250); // Соединить с точкой (175,250)
с.fillRect(100-3,200-3,6,6);           // Метка контрольной точки (100,200)
// Кубическая кривая Безье
c.moveTo(200, 250);                       // Начало в точке (200,250)
с.bezierCurveTo(220,220,280,280,300,250); // Соединить с точкой (300,250)
с.fillRect(220-3,220-3,6,6);              // Метки контрольных точек
с.fillRect(280-3.280-3,6,6);
// Определить некоторые графические атрибуты и нарисовать кривые
c.fillStyle = "#aaa"; // Серый цвет заливки
c.lineWidth = 5;      // Черные (по умолчанию) линии толщиной 5 пикселов
c.fill();             // Залить фигуры
c.stroke();           // Нарисовать контуры

Оглавление книги