Книга: JavaScript. Подробное руководство, 6-е издание

21.4.4.2. Примеры преобразований

21.4.4.2. Примеры преобразований

Пример 21.6 демонстрирует мощь, которую дает возможность преобразования системы координат, где за счет рекурсивного применения методов translate(), rotate() и scale() реализовано рисование фракталов - снежинок Коха. Результат работы этого примера представлен на рис. 21.8, где показаны снежинки Коха с количеством уровней рекурсии 0, 1, 2, 3 и 4.

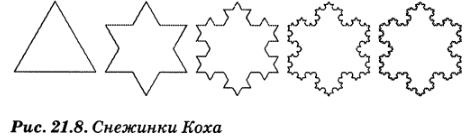
Эти фигуры воспроизводятся весьма изящным программным кодом, но в нем используются рекурсивные преобразования системы координат, что делает его сложным для понимания. Даже если вы не собираетесь углубляться в изучение всех тонкостей примера, обратите все же внимание, что в нем имеется всего один вызов метода lineTo(). Каждый отдельный сегмент на рис. 21.8 рисуется следующим образом:

с.lineТо(len, 0);

Значение переменной len не изменяется в ходе выполнения программы, поэтому позиция, ориентация и длина каждой линии определяется операциями смещения, вращения и масштабирования.

Пример 21.6. Рисование снежинок Коха посредством преобразований системы координат

var deg = Math.PI/180; // Для преобразования градусов в радианы
// Рисует n-уровневый фрактал снежинки Коха в контексте холста с, левый нижний угол
// которого имеет координаты (х,у), а длина стороны равна len.
function snowflake(c, п, х, у, len) {
  c.saveO; // Сохранить текущее преобразование
  с.translated,у); // Сместить начало координат в начальную точку
  с.moveTo(0,0); // Новый фрагмент контура в новом начале координат
  leg(n); // Нарисовать первую ветвь снежинки
  с.rotate(-120*deg); // Поворот на 120 градусов против часовой стрелки
  leg(n); // Нарисовать вторую ветвь
  с.rotate(-120*deg); //Поворот
  leg(n); // Нарисовать последнюю ветвь
  с.closePath(); // Замкнуть фрагмент контура
  c.restoreO; // Восстановить прежнее преобразование
  // Рисует одну ветвь n-уровневой снежинки Коха. Эта функция оставляет
  // текущую позицию в конце нарисованной ветви и смещает начало координат так,
  // что текущая точка оказывается в позиции (0,0).
  // Это означает, что после рисования ветви можно вызвать rotate().
  function leg(n) {
    c.save(); // Сохранить текущее преобразование
    if (n == 0) { // Нерекурсивный случай:
      с.lineTo(len, 0); // Просто нарисовать горизонтальную линию
    } //
    else { // Рекурсивный случай: 4 подветви вида: /
      с.scale(1/3,1/3); // Подветви в 3 раза меньше этой ветви
      leg(n-1); // Рекурсия для первой подветви
      с.rotate(60*deg); // Поворот на 60 градусов по часовой стрелке
      leg(n-1); // Вторая подветвь
      с.rotate(-120*deg); // Поворот на 120 градусов назад
      leg(n-1); // Третья подветвь
      с.rotate(60*deg); // Поворот обратно к началу
      leg(п-1); // Последняя подветвь
    }
    c.restore(); // Восстановить преобразование
    с.translate(len, 0); // Но сместить в конец ветви (0,0)
  }
}
snowf1аке(с,0,5,115,125); // Снежинка нулевого уровня является
                          // равносторонним треугольником
snowflake(c,1,145,115,125); // Снежинка первого уровня - шестиконечная звезда
snowflake(c,2,285,115,125); // и так далее.
snowflake(c,3,425.115.125);
snowflake(c,4,565,115,125); // Снежинка четвертого уровня выглядит как снежинка!
c.stroke(); // Нарисовать этот очень сложный контур

Оглавление книги