Книга: Как думают великие компании: три правила

Приложение С. Идентификация выдающихся показателей

Приложение С. Идентификация выдающихся показателей

Наша основная мера эффективности – это фондорентабельность (ФР) в течение всего срока существования компании, но мы учитываем также рост выручки (доходов) и совокупный доход акционеров (СДА). Для оценки относительной эффективности компаний по каждому показателю мы используем статистические методы.

Фондорентабельность (ФР)

В рамках нашей аналогии с подбрасыванием монеты легко рассчитать вероятность достижения того или иного результата, потому что мы знаем вероятность каждого из двух возможных результатов каждого подбрасывания: при каждом подбрасывании вероятности выпадения орла и решки составляют по 50 %. А какова вероятность того, что случайно выбранная компания, имеющая в этом году оценку 4 балла, в следующем году будет иметь оценку 7 баллов? Чтобы иметь возможность отвечать на подобные вопросы, мы построили матрицу 10 ? 10, в которую внесли наблюдаемые частоты всех вариантов изменения оценок компаний в следующем году по сравнению с предыдущим.

Перемещаясь по строке 1 в приведенной ниже таблице, мы увидим, что компании, которые имели оценку 0 баллов (по 10-балльной шкале) за 1-й год, с вероятностью 52,8 % заканчивают следующий год с той же оценкой. Вероятность получения оценки 1 балл составляет 18,2 % и так далее, вплоть до перехода к оценке 9 баллов, вероятность которого составляет 4,4 %. Очевидно, что чаще всего в следующем году компания получает ту же оценку, что и в предыдущем, причем у компаний с самыми высокими и самыми низкими оценками это проявляется особенно ярко.

Используя эти частотные вероятности, мы можем строить модели и определять вероятности любых заданных профилей рентабельности. Например, можно узнать вероятность получения пяти 5-балльных оценок на основании данных за семь лет, если в 1-й год компания имела оценку 7 баллов, или вероятность получения восьми 7-балльных оценок за 10 лет, если в 1-й год компания имела оценку 9 баллов. Однако такие расчеты имеют весьма ограниченное применение. Это совершенно аналогично расчету вероятности какого-либо конкретного числа последовательных выпадений орла при подбрасывании монеты. Каждый конкретный результат почти невероятен, но какой-то из них неизбежен. Конкретный результат имеет значение только тогда, когда он по своей природе является значимым для нас и при этом статистически неожиданным.

Таблица 45. Матрица изменений 10-балльных оценок (%)

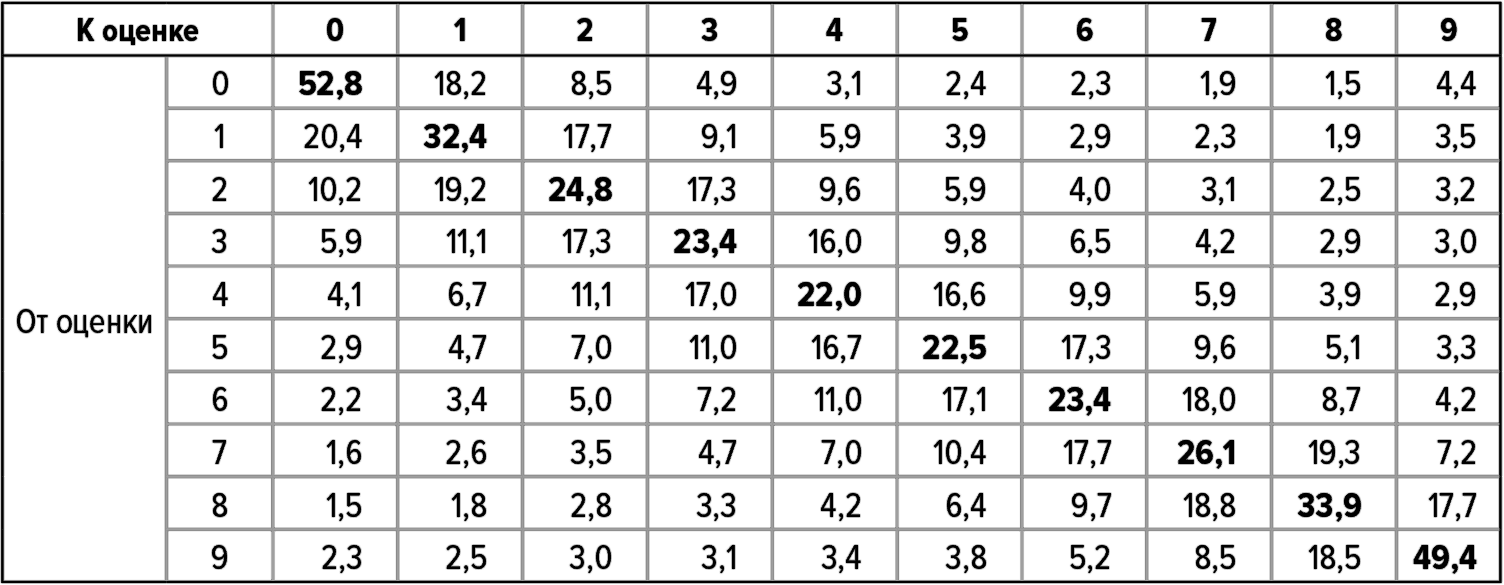
Источники: Compustat; анализ Deloitte.

Посмотрим на эту проблему под другим углом: компания может однажды получить оценку 9 баллов просто потому, что ей повезло, выпал счастливый случай. Но если она один раз получила оценку 9 баллов, то высока вероятность получения ею 9 баллов и в следующем году, просто потому, что 9-балльные результаты чаще повторяются. И теперь, когда компания получила уже две 9-балльные оценки подряд, мы не сможем сказать, что это просто эхо удачи, которая имела место в первый год. Пусть в первый год просто повезло, но со временем воздействие этого «повезло» исчезает, и поэтому вероятность того, что 9-балльные оценки повторяются просто в силу остаточного воздействия первоначальной удачи, исчезающе мала. Действительно, вероятность получения только 9-балльных оценок в течение 11 лет наблюдений чрезвычайно мала. Но именно реализация такого маловероятного случая и позволяет отнести компанию к категории «чудотворцев».

При этом необходимо, однако, принимать во внимание общее число компаний, которые наблюдались в течение этих 11 лет. Если в нашей базе данных сотни, а тем более тысячи компаний, то вероятность получения одной или даже несколькими компаниями одиннадцати 9-балльных оценок подряд в результате повторений удачи в сочетании с инерцией от каждого предыдущего позитивного импульса возрастает. Например, выпадение орла 11 раз подряд при подбрасывании симметричной монеты весьма маловероятно, однако достаточно довести число участников такого эксперимента всего лишь (примерно) до двух тысяч человек, чтобы – почти наверняка – хотя бы один человек получил такой результат. Итак, при достаточном числе испытаний почти невероятные события становятся достаточно вероятными, и, объясняя их появление какими-либо причинно-следственными связями, легко получить «ложноположительное» заключение.

Используя матрицу изменений 9-балльных оценок (таблица 45), мы выполнили 1000 имитаций для всех реально существовавших компаний, начиная с их фактических 9-балльных оценок и отслеживая частоту появления 9-балльных годовых оценок у компаний с разным сроком существования. Для иллюстрации: наша тысяча имитаций показала, что вероятность случайного получения компанией с 11-летней историей пяти и более годовых 9-балльных оценок составляет всего 4,3 %. Итак, подобный исход маловероятен, и поэтому, если мы видим компанию с пятью или более 9-балльными оценками за 11 лет наблюдений, мы с достаточной уверенностью можем предположить, что компания действительно продемонстрировала исключительную рентабельность.

Однако в нашей совокупности имеется 856 компаний со сроком существования 11 лет. И даже если для какой-либо конкретной компании вероятность получения пяти или более 9-балльных оценок составляет менее 5 %, мы по-прежнему должны ожидать увидеть в этой совокупности 37 компаний с пятью и более годовыми 9-балльными оценками просто потому, что таких «11-летних» компаний в ней очень много.

В нашей популяции имеется 45 компаний с пятью и более годовыми 9-балльными оценками за 11 лет. То есть таких компаний оказалось больше, чем можно было ожидать, и мы можем с некоторой долей уверенности заключить, что как минимум некоторые из них (скорее всего, 8) на самом деле являются выдающимися. К сожалению, у нас нет никакой возможности узнать, какие именно 8. Самое лучшее, что мы можем сделать, – это выбрать наугад 8 компаний из всей группы в 45 компаний, и смириться с 82 %-й вероятностью (37 из 45), что мы выбрали компании, которым просто повезло, то есть с 82 %-й вероятностью «ложноположительного» результата.

Для уменьшения вероятности появления ложноположительных результатов мы можем поднять планку – потребовать наличия более длинного ряда 9-балльных оценок для того же срока наблюдений, чтобы вероятность ложноположительного результата снизилась до желательного уровня. Мы определяем, что для попадания в категорию «чудотворцев» компания должна иметь такую цепочку годовых 9-балльных оценок, чтобы вероятность случайного сочетания таких оценок составляла менее 10 % и при этом вероятность ложноположительного результата тоже должна составлять менее 10 %.

Поскольку мы работаем с годовыми 9-балльными оценками, мы можем сравнивать рентабельность любой компании с рентабельностью любой другой компании в данном году. Используя матрицу изменений 10-балльных оценок для определения вероятности заданного числа 9-балльных оценок (для «чудотворцев») или 6-, 7– и 8-балльных оценок (для «стайеров») в течение заданного срока наблюдений, мы можем сравнить вероятность достижения выдающейся рентабельности любой компанией с аналогичной вероятностью для любой другой компании независимо от года ее основания и срока существования.

Ни в одном из наших критериев нет ничего предначертанного свыше. Почему вероятность отбраковки составляет 10 %? Почему не 5 или не 15 %? Почему нужно выделять «чудотворцев» только по 9-балльным годовым оценкам? Ведь можно было бы считать «чудотворцами», например, компании с 8– и 9-балльными оценками при маловероятной частоте их получения.

Практически для любого подобного набора параметров мы можем лишь интуитивно оценить его разумность. Важно то, что наше определение используется в контексте строгого статистического анализа: любая компания, для которой число случаев соответствия всем установленным критериям превышает число случаев, вытекающее из теории вероятностей, может претендовать на звание выдающейся компании. Чтобы наше исследование было (как минимум – потенциально) полезным, достаточно, чтобы показатели рентабельности, которые мы определили, имели адекватную доверительную валидность. Вы сами должны оценить, соответствуют ли выбранные нами критерии рентабельности вашим субъективным представлениям о том, каков должен быть уровень рентабельности, к которому стоит стремиться. В определенной степени этот выбор объясняется также здравым смыслом: если сделать критерии чересчур строгими, может оказаться, что у нас вообще не останется компаний, подлежащих исследованию; а если они будут слишком мягкими, то и полученные выводы окажутся недостаточно обоснованными{186}. В приведенной ниже таблице показано, в течение скольких лет компания должна получать заданную оценку в баллах (или оценки в заданном диапазоне баллов) при том или ином сроке существования, чтобы преодолеть пороговое значение 90 %-й вероятности.

В этих расчетах есть некоторые контринтуитивные аспекты, требующие дополнительного пояснения. Число лет, в течение которых компании необходимо получать целевые оценки в баллах (или оценки в целевом диапазоне баллов), не увеличивается монотонно с увеличением срока существования компании. Отметим, например, что если компания существует 20 лет, то для зачисления в «чудотворцы» она должна получить 12 годовых 9-балльных оценок, если компания существует 30 лет, то число необходимых 9-балльных оценок снижается до 10, а если она существует уже 45 лет, оно снова увеличивается до 16. Это связано с нашим методом коррекции проблемы ложноположительных результатов, а также так называемой систематической ошибки выжившего (survivor bias).

Таблица 46. Число целевых годовых оценок по 10-балльной шкале, необходимое для достижения статуса «чудотворца»

Источники: Compustat; анализ Deloitte.

Исходя из матрицы изменений 10-балльных оценок, для получения статуса «чудотворца» компании, данные по которой имеются за 35 лет, требуется больше годовых 9-балльных оценок, чем компании, данные по которой имеются за 20 лет; однако компаний с данными за 20 лет больше, чем компаний с данными за 35 лет, поэтому чтобы снизить вероятность получения ложноположительного результата до 10 %, нам необходимо «поднять планку» для компаний с данными за 20 лет.

Неожиданно большие значения для компаний с данными за 45 лет связаны со сравнительно большим числом таких компаний в нашей совокупности; многие из них возникли еще до 1966 г. (начало нашей базы данных) и все еще существовали в 2010 г. (конец нашей базы данных). Наши значения квантильной регрессии отражают как минимум некоторые воздействия выживаемости на ФР, но даже в этом случае если эти компании-долгожители имеют какие-то отличительные особенности, то, компенсируя большее число таких компаний ужесточением критериев, мы снижаем вероятность систематической ошибки выжившего.

СДА и рост выручки

Для выявления в статистическом смысле исключительных значений роста выручки и СДА требуется иной подход, поскольку при определении рентабельности компании в течение определенного периода необходимо учитывать кумулятивность: кумулятивный годовой рост от года 0 до года 2 зависит от показателей, достигнутых компанией и в 1-й год, и во 2-й год. Поэтому компания может продемонстрировать заоблачный относительный рост в течение 2-го года (например, рост на 50 %), даже если она вообще практически не росла в предыдущие два года (годы 0 и 1), и это означает, что ее рост в течение 2-го года рассчитывается на основании слишком малой базы. Исходя из этого, мы решили, что наш подход с использованием 10-балльных годовых оценок здесь неуместен. В самом деле, возьмем экстремальный пример: компания, у которой годы 50 %-го «усыхания» чередуются с годами 100 %-го роста при анализе половины данных, соответствующих бурному росту (согласно критериям выявления выдающейся рентабельности), будет характеризоваться очень быстрым ростом, хотя ее общий рост за этот период составит 0 %.

Вместо этого мы строили регрессионные модели отдельно для роста выручки и для СДА (на концептуальном уровне оба этих показателя анализируются одинаково). Эта регрессия позволяет прогнозировать рентабельность, которую данная компания «должна иметь» в данном году в зависимости от ее размеров, года, отрасли, срока существования и показателей за предыдущий год. В каждом конкретном году фактическая рентабельность компании обычно отклоняется от прогнозируемого значения и оказывается либо выше его (положительный остаток), либо ниже его (отрицательный остаток). Сумма этих остатков образует кумулятивный остаток компании, или «сырую» R-оценку.

Однако напрямую сравнивать «сырые» R-оценки мы не можем. Две компании, имеющие одинаковые годовые R-оценки, получат разные агрегированные оценки, если у них разные сроки существования: если R-оценки роста у компаний А и В составляют, скажем, 5 % в год, но компания А существует 15 лет, а компания В – 20 лет, то компания В будет иметь более высокую R-оценку просто в силу большей длительности ее существования, а не в силу более интенсивного роста. Для коррекции этого несоответствия мы используем моделирование, позволяющее определить ожидаемую R-оценку для компаний с разной длительностью наблюдений. Таким образом мы получаем «исправленные» R-оценки для всех компаний, уже сопоставимые между собой. Затем мы упорядочиваем эти исправленные R-оценки, ранжируя каждую компанию по СДА и росту выручки с учетом срока ее существования.

Оглавление книги