Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Механистический мир динамики Ньютона
Механистический мир динамики Ньютона
С введением определенного закона для силы (как обратного квадрата расстояния между телами) ньютоновская модель превращается в точную и определенную систему динамических уравнений. Если положения, скорости и массы различных частиц заданы в некоторый момент времени, то их положения и скорости (равно как и массы, которые считаются постоянными) автоматически определены для всех последующих моментов времени. Эта форма детерминизма, которой удовлетворяет мир механики Ньютона, оказала (и все еще продолжает оказывать) глубокое влияние на философскую мысль. Попробуем изучить природу ньютонианского детерминизма чуть более подробно. Что он может сказать нам о «свободе воли»? Мог бы в строго ньютонианском мире существовать разум? Найдется ли в нем место хотя бы компьютерам?
Давайте попытаемся представить более конкретно «ньютонианскую» модель мира. Например, мы можем предположить, что частицы материи допустимо считать математическими точками, т. е. объектами, не имеющими никакой пространственной протяженности. В качестве альтернативы все частицы можно считать твердыми сферическими шариками. И в том, и в другом случае нам придется предположить, что законы действия сил, как в случае ньютоновского закона всемирного тяготения, известны. Мы хотим промоделировать и другие встречающиеся в природе силы, такие как электрические и магнитные взаимодействия (впервые подробно исследованные в 1600 году Уильямом Гильбертом), или сильные ядерные взаимодействия, которые, как ныне известно, связывают частицы (протоны и нейтроны), образующие атомные ядра. Электрическое взаимодействие похоже на гравитационное, поскольку тоже удовлетворяет закону обратных квадратов, но при этом одинаково заряженные частицы отталкивают (а не притягивают, как в случае гравитационного взаимодействия) друг друга, и величину электрического взаимодействия определяют не массы, а электрические заряды частиц. Магнитное взаимодействие, так же как и электрическое, «обратно пропорционально квадрату расстояния»[108], но ядерное взаимодействие имеет совершенно другую зависимость от расстояния: оно очень велико на очень малых расстояниях, сравнимых с внутриатомными, и пренебрежимо мало на бо?льших расстояниях.
Предположим, что мы остановили свой выбор на модели твердых сферических шариков, потребовав, чтобы при столкновении частиц шарики просто идеально упруго отражались. Иначе говоря, они должны разлетаться после столкновения без какой бы то ни было потери энергии (или полного количества движения (импульса)), как если бы они были идеальными бильярдными шарами. Нам необходимо также точно задать, какие силы должны действовать между шариками. Для простоты мы можем положить, что сила, с которой один шарик действует на любой другой, направлена по прямой, соединяющей центры шариков, а величина силы определяется длиной отрезка между центрами шариков. (Для ньютоновской гравитации это предположение выполняется автоматически в силу замечательной теоремы, доказанной Ньютоном; а для других видов сил оно может быть наложено в качестве дополнительного требования.) Если шарики сталкиваются только попарно, а тройные столкновения, как и столкновения более высокого порядка, не происходят, то все вполне определено, и исход столкновения непрерывно зависит от начального состояния (т. е. достаточно малые изменения в начальном состоянии приводят лишь к малым изменениям в конечном). Скользящие столкновения рассматриваются как предельный случай прохождения шариков в непосредственной близости друг от друга. Проблема возникает при рассмотрении тройных столкновений и столкновений более высоких порядков. Например, если происходит одновременное столкновение трех шариков А, В и С, то вся картина значительно меняется в зависимости от того, какое из попарных соударений мы рассматриваем сначала: шарика А с шариком В, а сразу же после этого — С с В; или же мы считаем, что сначала сталкиваются шарики А и С, а затем шарик В сталкивается с шариком А (рис. 5.8).
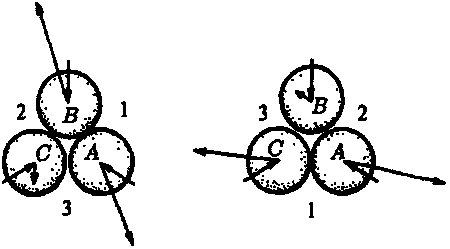
Рис. 5.8. Тройное соударение. Поведение частиц в результате столкновения существенно зависит от того, какие частицы сталкиваются первыми, поэтому исход столкновения не зависит непрерывным образом от начальных данных
В нашей модели существует индетерминизм, когда происходит тройное столкновение! Если угодно, то мы можем просто исключить тройные столкновения и столкновения более высокого порядка как «в высшей степени (бесконечно) невероятные». Это дает вполне непротиворечивую схему, но потенциальная проблема тройных столкновений означает, что результирующее поведение частиц может не зависеть непрерывным образом от начального состояния.
Поскольку такое положение дел нас не совсем удовлетворяет, то мы можем отдать предпочтение картине точечных частиц. Но для того, чтобы избежать некоторых теоретических трудностей, возникающих в рамках этого подхода (бесконечные силц и бесконечные энергии при столкновении частиц), необходимо сделать дополнительные предположения, в частности о том, что на коротких расстояниях силы, действующие между частицами, всегда становятся отталкивающими. Тогда мы можем обеспечить невозможность столкновения любой пары частиц. (Оно также помогает нам избежать проблемы определения поведения частиц при столкновении!) Но для большей наглядности я все-таки буду рассматривать модель твердых сферических шариков, ибо, как мне кажется, подобная «бильярдная» картина для большинства из нас подсознательно как раз и является рабочей моделью реальности!
Подчеркнем (игнорируя проблему столкновения нескольких шариков), что ньютонианская[109] бильярдная картина реальности в действительности является детерминистской моделью. Слово «детерминистская» надлежит понимать в том смысле, что физическое поведение системы с математической точки зрения полностью определено во все моменты времени в будущем (или в прошлом) положениями и скоростями шариков (во избежание некоторых проблем предположим, что число шариков конечно) в какой-то один момент времени. Таким образом, создается впечатление, будто в таком бильярдном мире нет места для разума, который своей «свободной волей» мог бы влиять на поведение материальных объектов. Если мы верим в «свободу воли», то, по-видимому, вынуждены будем усомниться в возможности описания нашего реального мира в рамках бильярдной модели.
Мучительный вопрос о «свободе воли» проходит через всю эту книгу — хотя при обсуждении большинства затронутых в ней тем он остается на заднем плане. В этой главе ему предстоит сыграть определенную, но небольшую роль (связанную с проблемой передачи сигналов со сверхсветовой скоростью в теории относительности). Вопросом о свободе воли мы займемся непосредственно в главе 10, и читатель несомненно будет разочарован моим вкладом в эту проблему. Я действительно считаю, что вопрос о свободе воле представляет собой реальную, а не вымышленную проблему — но она в высшей степени нетривиальна и ее трудно сформулировать адекватно. Вопрос о детерминизме в физической теории, безусловно, важен, однако я убежден, что он не является камнем преткновения. Например, мир может быть детерминистским, но невычислимым. Иначе говоря, будущее может определяться прошлым, но точно рассчитать его при этом будет в принципе невозможно. В главе 10 я попытаюсь изложить аргументы, показывающие, что действие нашего наделенного сознанием разума неалгоритмично (т. е. невычислимо). Соответственно, свобода воли, которой мы наделены (по нашему глубокому убеждению), должна быть тесно связана с какой-то невычислимой составляющей законов, управляющих тем миром, в котором мы живем. Независимо от того, принимаем ли мы или отвергаем такую точку зрения на свободу воли, интерес для нас представляет вопрос именно о вычислимости данной физической теории (например, ньютоновской динамики), а не о том, является ли она детерминистской. Вопрос о вычислимости отличен от вопроса о детерминизме. Утверждение о том, что это — два совершенно разных вопроса, как раз и служит одним из основных тезисов в данной книге.
- Состояние физической теории
- Евклидова геометрия
- Динамика Галилея и Ньютона
- Механистический мир динамики Ньютона
- Вычислима ли жизнь в бильярдном мире?
- Гамильтонова механика
- Фазовое пространство
- Электромагнитная теория Максвелла
- Вычислимость и волновое уравнение
- Уравнение движения Лоренца; убегающие частицы
- Специальная теория относительности Эйнштейна и Пуанкаре
- Общая теория относительности Эйнштейна
- Релятивистская причинность и детерминизм
- Вычислимость в классической физике: где мы находимся?
- Масса, материя и реальность
- Глава 5 Классический мир
- 8.2. Языки программирования Виды программирований
- 1.1. Введение в объектно-ориентированное программирование
- Покупатель на крючке. Руководство по созданию продуктов, формирующих привычки
- Язык программирования Python
- Формирование платежного поручения
- Программирование на языке Пролог для искусственного интеллекта
- 4.2. Формирование концепции репутационного менеджмента
- Программируя Вселенную. Квантовый компьютер и будущее науки
- Команды и формирование культуры по инициативе сверху
- 6.7. Формирование составных целевых утверждений
- Глава 1 Предел возможностей иерархии в мире перемен




