Книга: Новый ум короля: О компьютерах, мышлении и законах физики
Общая теория относительности Эйнштейна
Общая теория относительности Эйнштейна
Напомним великую истину, открытую Галилеем: все тела под действием силы тяжести падают одинаково быстро. (Это было блестящей догадкой, едва ли подсказанной эмпирическими данными, поскольку из-за сопротивления воздуха перья и камни все же падают не одновременно! Галилей внезапно понял, что, если бы сопротивление воздуха можно было свести к нулю, то перья и камни падали бы на Землю одновременно.) Потребовалось три столетия, прежде чем глубокое значение этого открытия было по достоинству осознано и стало краеугольным камнем великой теории. Я имею в виду общую теорию относительности Эйнштейна — поразительное описание гравитации, для которого, как нам вскоре станет ясно, потребовалось введение понятия искривленного пространства-времени!
Какое отношение имеет интуитивное открытие Галилея к идее «кривизны пространства-времени»? Каким образом могло получиться, что эта концепция, столь явно отличная от схемы Ньютона, согласно которой частицы ускоряются под действием обычных гравитационных сил, оказалась способной не только сравняться в точности описания с ньютоновской теорией, но и превзойти последнюю? И потом, насколько верным будет утверждение, что в открытии Галилея было нечто такое, что не было позднее включено в ньютоновскую теорию?
Позвольте мне начать с последнего вопроса потому, что ответить на него проще всего. Что, согласно теории Ньютона, управляет ускорением тела под действием гравитации? Во-первых, на тело действует гравитационная сила, которая, как гласит открытый Ньютоном закон всемирного тяготения, должна быть пропорциональна массе тела. Во-вторых, величина ускорения, испытываемая телом под действием заданной силы, по второму закону Ньютона, обратно пропорциональна массе тела. Удивительное открытие Галилея зависит от того факта, что «масса», входящая в открытый Ньютоном закон всемирного тяготения, есть, в действительности, та же «масса», которая входит во второй закон Ньютона. (Вместо «та же» можно было бы сказать «пропорциональна».) В результате ускорение тела под действием гравитации не зависит от его массы. В общей схеме Ньютона нет ничего такого, что указывало бы, что оба понятия массы одинаковы. Эту одинаковость Ньютон лишь постулировал. Действительно, электрические силы аналогичны гравитационным в том, что и те, и другие обратно пропорциональны квадрату расстояния, но электрические силы зависят от электрического заряда, который имеет совершенно другую природу, чем масса во втором законе Ньютона. «Интуитивное открытие Галилея» было бы неприменимо к электрическим силам: о телах (заряженных телах) брошенных в электрическом поле, нельзя сказать, что они «падают» с одинаковой скоростью!
На время просто примем интуитивное открытие Галилея относительно движения под действием гравитации и попытаемся выяснить, к каким следствиям оно приводит. Представим себе Галилея, бросающего с Пизанской наклонной башни два камня. Предположим, что с одним из камней жестко скреплена видеокамера, направленная на другой камень. Тогда на пленке окажется запечатленной следующая ситуация: камень парит в пространстве, как бы не испытывая действия гравитации (рис. 5.23)! И так происходит именно потому, что все тела под действием гравитации падают с одной и той же скоростью.
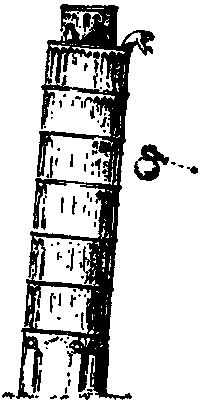
Рис. 5.23. Галилей бросает два камня (и видеокамеру) с Пизанской башни
В описанной выше картине мы пренебрегаем сопротивлением воздуха. В наше время космические полеты открывают перед нами лучшую возможность проверки этих идей, так как в космическом пространстве нет воздуха. Кроме того, «падение» в космическом пространстве означает просто движение по определенной орбите под действием гравитации. Такое «падение» совсем не обязательно должно происходить по прямой вниз — к центру Земли. В нем вполне может быть и некоторая горизонтальная составляющая. Если эта горизонтальная составляющая достаточно велика, то тело может «падать» по круговой орбите вокруг Земли, не приближаясь к ее поверхности! Путешествие по свободной околоземной орбите под действием гравитации — весьма изощренный (и очень дорогой!) способ «падения». Как в описанной выше видеозаписи, астронавт, совершая «прогулку в открытом космосе», видит свой космический корабль парящим перед собой и как бы не испытывающим действия гравитации со стороны огромного шара Земли под ним! (См. рис. 5.24.) Таким образом, переходя в «ускоренную систему отсчета» свободного падения, можно локально исключить действие гравитации.

Рис. 5.24. Астронавт видит, что его космический корабль парит перед ним, как будто неподверженный действию гравитации
Мы видим, что свободное падение позволяет исключить гравитацию потому, что эффект от действия гравитационного поля такой же, как от ускорения Действительно, если вы находитесь в лифте, который движется с ускорением вверх, то вы просто ощущаете, что кажущееся гравитационное поле увеличивается, а если лифт движется с ускорением вниз, то вам кажется, что гравитационное поле убывает. Если бы трос, на котором подвешена кабина, оборвался, то (если пренебречь сопротивлением воздуха и эффектами трения) результирующее ускорение, направленное вниз (к центру Земли), полностью уничтожило бы действие гравитации, и люди, оказавшиеся в кабине лифта, стали бы свободно плавать в пространстве, подобно астронавту во время выхода в открытый космос, до тех пор, пока кабина не стукнулась бы о Землю! Даже в поезде или на борту самолета ускорения могут быть такими, что ощущения пассажира относительно величины и направления гравитации могут не совпадать с тем, где, как показывает обычный опыт, должны быть «верх» и «низ». Объясняется это тем, что действия ускорения и гравитации схожи настолько, что наши ощущения не способны отличить одни от других. Этот факт — то, что локальные проявления гравитации эквивалентны локальным проявлениям ускоренно движущейся системы отсчета, — и есть то, что Эйнштейн назвал принципом эквивалентности.
Приведенные выше соображения «локальны». Но если разрешается производить (не только локальные) измерения с достаточно высокой точностью, то в принципе можно установить различие между «истинным» гравитационным полем и чистым ускорением. На рис. 5 25 я изобразил в немного преувеличенном виде, как первоначально стационарная сферическая конфигурация частиц, свободно падающая под действием гравитации, начинает деформироваться под влиянием неоднородности (ньютоновского) гравитационного поля.
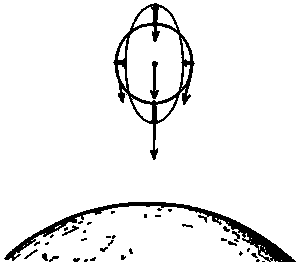
Рис. 5.25. Приливный эффект. Двойные стрелки указывают относительное ускорение (ВЕЙЛЬ)
Это поле неоднородно в двух отношениях. Во-первых, поскольку центр Земли расположен на некотором конечном расстоянии от падающего тела, частицы, расположенные ближе к поверхности Земли, движутся вниз с бо?льшим ускорением, чем частицы, расположенные выше (напомним закон обратной пропорциональности квадрату расстояния Ньютона). Во-вторых, по той же причине существуют небольшие различия в направлении ускорения для частиц, занимающих различные положения на горизонтали. Из-за этой неоднородности сферическая форма начинает слегка деформироваться, превращаясь в «эллипсоид». Первоначальная сфера удлиняется в направлении к центру Земли (а также в противоположном направлении), так как те ее части, которые ближе к центру Земли, движутся с чуть бо?льшим ускорением, чем те части, которые дальше от центра Земли, и сужается по горизонтали, так как ускорения ее частей, находящихся на концах горизонтального диаметра, слегка скошены «внутрь» — в направлении на центр Земли.
Это деформирующее действие известно как приливный эффект гравитации. Если мы заменим центр Земли Луной, а сферу из материальных частиц — поверхностью Земли, то получим в точности описание действия Луны, вызывающей приливы на Земле, причем «горбы» образуются по направлению к Луне и от Луны. Приливный эффект — общая особенность гравитационных полей, которая не может быть «исключена» с помощью свободного падения. Приливный эффект служит мерой неоднородности ньютоновского гравитационного поля. (Величина приливной деформации в действительности убывает обратно пропорционально кубу, а не квадрату расстояния от центра притяжения.)
Закон всемирного тяготения Ньютона, по которому сила обратно пропорциональна квадрату расстояния, допускает, как оказывается, простую интерпретацию в терминах приливного эффекта: объем эллипсоида, в который первоначально[126] деформируется сфера, равен объему исходной сферы — в предположении, что сфера окружает вакуум. Это свойство сохранения объема характерно для закона обратных квадратов; ни для каких других законов оно не выполняется. Предположим далее, что исходная сфера окружает не вакуум, а некоторое количество материи общей массой М. Тогда возникает дополнительная компонента ускорения, направленная внутрь сферы из-за гравитационного притяжения материи внутри сферы. Объем эллипсоида, в который первоначально деформируется наша сфера из материальных частиц, сокращается — на величину, пропорциональнуюМ. С примером эффекта уменьшения объема эллипсоида мы бы столкнулись, если бы выбрали нашу сферу так, чтобы она окружала Землю на постоянной высоте (рис. 5.26). Тогда обычное ускорение, обусловленное земным притяжением и направленное вниз (т. е. внутрь Земли), будет той самой причиной, по которой происходит сокращение объема нашей сферы.
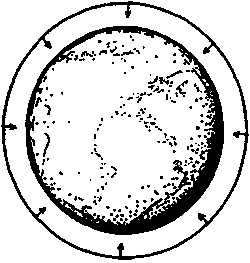
Рис. 5.26. Когда сфера окружает некое вещество (в данном случае — Землю), возникает результирующее ускорение, направленное внутрь (РИЧЧИ)
В этом свойстве сжимания объема заключена оставшаяся часть закона всемирного тяготения Ньютона, а именно — что сила пропорциональна массе притягивающего тела.
Попробуем получить пространственно-временну?ю картину такой ситуации. На рис. 5.27 я изобразил мировые линии частиц нашей сферической поверхности (представленной на рис. 5.25 в виде окружности), причем я использовал для описания ту систему отсчета, в которой центральная точка сферы кажется покоящейся («свободное падение»).

Рис. 5.27. Кривизна пространства-времени: приливный эффект, изображенный в пространстве-времени
Позиция общей теории относительности состоит в том, чтобы считать свободное падение «естественным движением» — аналогичным «равномерному прямолинейному движению», с которыми имеют дело в отсутствие гравитации. Таким образом, мы пытаемся описывать свободное падение «прямыми» мировыми линиями в пространстве-времени! Но если взглянуть на рис. 5.27, то становится понятно, что использование слова «прямые» применительно к этим мировым линиям способно ввести читателя в заблуждение, поэтому мы будем в терминологических целях называть мировые линии свободно падающих частиц в пространстве-времени — геодезическими.
Но насколько хороша такая терминология? Что обычно понимают под «геодезической» линией? Рассмотрим аналогию для двумерной искривленной поверхности. Геодезическими называются такие кривые, которые на данной поверхности (локально) служат «кратчайшими маршрутами». Иначе говоря, если представить себе отрезок нити, натянутый на указанную поверхность (и не слишком длинный, чтобы он не мог соскользнуть), то нить расположится вдоль некоторой геодезической линии на поверхности.
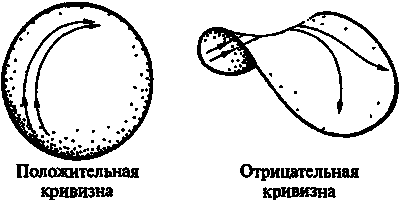
Рис. 5.28. Геодезические линии в искривленном пространстве: линии сходятся в пространстве с положительной кривизной, и расходятся — в пространстве с отрицательной кривизной
На рис. 5.28 я привел два примера поверхностей: первая (слева) — поверхность так называемой «положительной кривизны» (как поверхность сферы), вторая — поверхность «отрицательной кривизны» (седловидная поверхность). На поверхности положительной кривизны две соседние геодезические линии, выходящие из начальных точек параллельно друг другу, начинают впоследствии изгибаться навстречу друг другу; а на поверхности отрицательной кривизны они изгибаются в стороны друг от друга.
Если мы представим себе, что мировые линии свободно падающих частиц в некотором смысле ведут себя как геодезические линии на поверхности, то окажется, что существует тесная аналогия между гравитационным приливным эффектом, о котором шла речь выше, и эффектами кривизны поверхности — причем как положительной кривизны, так и отрицательной. Взгляните на рис. 5.25, 5.27. Мы видим, что в нашем пространстве-времени геодезические линии начинают расходиться в одном направлении (когда они «выстраиваются» в сторону Земли) — как это происходит на поверхности отрицательной кривизны на рис. 5.28 — и сближаться в других направлениях (когда они смещаются горизонтально относительно Земли) — как на поверхности положительной кривизны на рис. 5.28. Таким образом, создается впечатление, что наше пространство-время, как и вышеупомянутые поверхности, тоже обладает «кривизной», только более сложной, поскольку из-за высокой размерности пространства-времени при различных перемещениях она может носить смешанный характер, не будучи ни чисто положительной, ни чисто отрицательной.
Отсюда следует, что понятие «кривизны» пространства-времени может быть использовано для описания действия гравитационных полей. Возможность использования такого описания в конечном счете следует из интуитивного открытия Галилея (принципа эквивалентности) и позволяет нам исключить гравитационную «силу» с помощью свободного падения. Действительно, ничто из сказанного мной до сих пор не выходит за рамки ньютонианской теории. Нарисованная только что картина дает просто переформулировку этой теории[127]. Но когда мы пытаемся скомбинировать новую картину с тем, что дает предложенное Минковским описание специальной теории относительности — геометрии пространства-времени, которая, как мы знаем, применяется в отсутствие гравитации — в игру вступает новая физика. Результат этой комбинации — общая теория относительности Эйнштейна.
Напомним, чему учил нас Минковский. Мы имеем (в отсутствие гравитации) пространство-время, наделенное особого рода мерой «расстояния» между точками: если мы имеем в пространстве-времени мировую линию, описывающую траекторию какой-нибудь частицы, то «расстояние» в смысле Минковского, измеряемое вдоль этой мировой линии, дает время, реально прожитое частицей. (В действительности, в предыдущем разделе мы рассматривали это «расстояние» только для тех мировых линий, которые состоят из прямолинейных отрезков — но приведенное выше утверждение справедливо и по отношению к искривленным мировым линиям, если «расстояние» измеряется вдоль кривой.) Геометрия Минковского считается точной, если нет гравитационного поля, т. е. если у пространства-времени нет кривизны. Но при наличии гравитации мы рассматриваем геометрию Минковского уже лишь как приближенную — аналогично тому, как плоская поверхность лишь приблизительно соответствует геометрии искривленной поверхности. Вообразим, что, изучая искривленную поверхность, мы берем микроскоп, дающий все большее увеличение — так, что геометрия искривленной поверхности кажется все больше растянутой. При этом поверхность будет нам казаться все более плоской. Поэтому мы говорим, что искривленная поверхность имеет локальное строение евклидовой плоскости[128]. Точно так же мы можем сказать, что при наличии гравитации пространство-время локально описывается геометрией Минковского (которая есть геометрия плоского пространства-времени), но мы допускаем некоторую «искривленность» на более крупных масштабах (рис. 5.29).
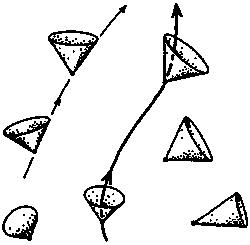
Рис. 5.29. Картина искривленного пространства-времени
В частности, как и в пространстве Минковского, любая точка пространства-времени является вершиной светового конуса — но в данном случае эти световые конусы расположены уже не одинаково. В главе 7 мы познакомимся с отдельными моделями пространства-времени, в которых явно видна эта неоднородность расположения световых конусов (см. рис. 7.13, 7.14). Мировые линии материальных частиц всегда направлены внутрь световых конусов, а линии фотонов — вдоль световых конусов. Вдоль любой такой кривой мы можем ввести «расстояние» в смысле Минковского, которое служит мерой времени, прожитого частицами так же, как и в пространстве Минковского. Как и в случае искривленной поверхности, эта мера «расстояния» определяет геометрию поверхности, которая может отличаться от геометрии плоскости.
Геодезическим линиям в пространстве-времени теперь можно придать интерпретацию, аналогичную интерпретации геодезических линий на двумерных поверхностях, учитывая при этом различия между геометриями Минковского и Евклида. Таким образом, наши геодезические линии в пространстве-времени представляют собой не (локально) кратчайшие кривые, а наоборот — кривые, которые (локально) максимизируют «расстояние» (т. е. время) вдоль мировой линии. Мировые линии частиц, свободно перемещающиеся под действием гравитации, согласно этому правилу действительно являются геодезическими. В частности, небесные тела, движущиеся в гравитационном поле, хорошо описываются подобными геодезическими линиями. Кроме того, лучи света (мировые линии фотонов) в пустом пространстве так же служат геодезическими линиями, но на этот раз — нулевой «длины»[129]. В качестве примера я схематически нарисовал на рис. 5.30 мировые линии Земли и Солнца. Движение Земли вокруг Солнца описывается «штопорообразной» линией, навивающейся вокруг мировой линии Солнца. Там же я изобразил фотон, приходящий на Землю от далекой звезды. Его мировая линия кажется слегка «изогнутой» вследствие того, что свет (по теории Эйнштейна) на самом деле отклоняется гравитационным полем Солнца.
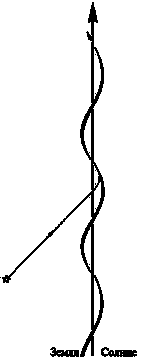
Рис. 5.30. Мировые линии Земли и Солнца. Световой луч от далекой звезды отклоняется Солнцем
Нам необходимо еще выяснить, каким образом ньютоновский закон обратных квадратов может быть включен (после надлежащей модификации) в общую теорию относительности Эйнштейна. Обратимся еще раз к нашей сфере из материальных частиц, падающей в гравитационном поле. Напомним, что если внутри сферы заключен только вакуум, то, согласно теории Ньютона, объем сферы первоначально не изменяется; но если внутри сферы находится материя общей массой М, то происходит сокращение объема, пропорциональное М. В теории Эйнштейна (для малой сферы) правила в точности такие же, за исключением того, что не все изменение объема определяется массой М; существует (обычно очень малый) вклад от давления, возникающем в окруженном сферой материале.
Полное математическое выражение для кривизны четырехмерного пространства-времени (которая должна описывать приливные эффекты для частиц, движущихся в любой данной точке по всевозможным направлениям) дается так называемым тензором кривизны Римана. Это несколько сложный объект; для его описания необходимо в каждой точке указать двадцать действительных чисел. Эти двадцать чисел называются его компонентами. Различные компоненты соответствуют различным кривизнам в различных направлениях пространства-времени. Тензор кривизны Римана обычно записывают в виде Rtjkl, но так как мне не хочется объяснять здесь, что означают эти субиндексы (и, конечно, что такое тензор), то я запишу его просто как:
РИМАН.
Существует способ, позволяющий разбить этот тензор на две части, называемые, соответственно, тензором ВЕЙЛЯ и тензором РИЧЧИ (каждый — с десятью компонентами). Условно я запишу это разбиение так:
РИМАН = ВЕЙЛЬ + РИЧЧИ.
(Подробная запись тензоров Вейля и Риччи для наших целей сейчас совершенно не нужна.) Тензор Вейля ВЕЙЛЬ служит мерой приливной деформации нашей сферы из свободно падающих частиц (т. е. изменения начальной формы, а не размеров); тогда как тензор Риччи РИЧЧИ служит мерой изменения первоначального объема[130]. Напомним, что ньютоновская теория гравитации требует, чтобы масса, содержащаяся внутри нашей падающей сферы, была пропорциональна этому изменению первоначального объема. Это означает, что, грубо говоря, плотность массы материи — или, что эквивалентно, плотность энергии (так как Е = mc2) — следует приравнять тензору Риччи.
По существу, это именно то, что утверждают уравнения поля общей теории относительности, а именно — полевые уравнения Эйнштейна[131]. Правда, здесь имеются некоторые технические тонкости, в которые нам сейчас, впрочем, лучше не вдаваться. Достаточно сказать, что существует объект, называемый тензором энергии-импульса, который объединяет всю существенную информацию об энергии, давлении и импульсе материи и электромагнитных полей. Я буду называть этот тензор ЭНЕРГИЕЙ. Тогда уравнения Эйнштейна весьма схематично можно представить в следующем виде,
РИЧЧИ = ЭНЕРГИЯ.
(Именно наличие «давления» в тензоре ЭНЕРГИЯ вместе с некоторыми требованиями непротиворечивости уравнений в целом приводят с необходимостью к учету давления в описанном выше эффекте сокращения объема.)
Кажется, что вышеприведенное соотношение ничего не говорит о тензоре Вейля. Тем не менее, оно отражает одно важное свойство. Приливный эффект, производимый в пустом пространстве, обусловлен ВЕЙЛЕМ. Действительно, из приведенных выше уравнений Эйнштейна следует, что существуют дифференциальные уравнения, связывающие ВЕЙЛЯ с ЭНЕРГИЕЙ — практически как во встречавшихся нам ранее уравнениях Максвелла[132]. Действительно, точка зрения, согласно которой ВЕЙЛЯ надлежит рассматривать как своего рода гравитационный аналог электромагнитного поля (в действительности, тензора — тензора Максвелла), описываемого парой (Е, В), оказывается весьма плодотворной. В этом случае ВЕЙЛЬ служит своего рода мерой гравитационного поля. «Источником» для ВЕЙЛЯ является ЭНЕРГИЯ — подобно тому, как источником для электромагнитного поля (Е, В) является (?, j) — набор из зарядов и токов в теории Максвелла. Эта точка зрения будет полезна нам в главе 7.
Может показаться весьма удивительным, что при столь существенных различиях в формулировке и основополагающих идеях, оказывается довольно трудно найти наблюдаемые различия между теориями Эйнштейна и теорией, выдвинутой Ньютоном двумя с половиной столетиями раньше. Но если рассматриваемые скорости малы по сравнению со скоростью света с, а гравитационные поля не слишком сильны (так, что скорости убегания гораздо меньше с, см. главу 7, «Динамика Галилея и Ньютона»), то теория Эйнштейна по существу дает те же результаты, что и теория Ньютона. Но в тех ситуациях, когда предсказания этих двух теорий расходятся, прогнозы теории Эйнштейна оказываются точнее. К настоящему времени был проведен целый ряд весьма впечатляющих экспериментальных проверок, которые позволяют считать новую теорию Эйнштейна вполне обоснованной. Часы, согласно Эйнштейну, в гравитационном поле идут чуть медленнее. Ныне этот эффект измерен непосредственно несколькими способами. Световые и радиосигналы действительно изгибаются вблизи Солнца и слегка запаздывают для наблюдателя, движущегося им навстречу. Эти эффекты, предсказанные изначально общей теорией относительности, на сегодняшний день подтверждены опытом. Движение космических зондов и планет требуют небольших поправок к ньютоновским орбитам, как это следует из теории Эйнштейна — эти поправки сегодня также проверены опытным путем. (В частности, аномалия в движении планеты Меркурия, известная как «смещение перигелия», беспокоившая астрономов с 1859 года, была объяснена Эйнштейном в 1915 году.) Возможно, наиболее впечатляющим из всего следует считать серию наблюдений над системой, называемой двойным пульсаром, которая состоит из двух небольших массивных звезд (возможно, двух «нейтронных звезд», см. гл.7 «Черные дыры»). Эта серия наблюдений очень хорошо согласуется с теорией Эйнштейна и служит прямой проверкой эффекта, полностью отсутствующего в теории Ньютона, — испускания гравитационных волн. (Гравитационная волна представляет собой аналог электромагнитной волны и распространяется со скоростью света с.) Не существует проверенных наблюдений, которые противоречили бы общей теории относительности Эйнштейна. При всей своей странности (на первый взгляд), теория Эйнштейна работает и по сей день!
- Состояние физической теории
- Евклидова геометрия
- Динамика Галилея и Ньютона
- Механистический мир динамики Ньютона
- Вычислима ли жизнь в бильярдном мире?
- Гамильтонова механика
- Фазовое пространство
- Электромагнитная теория Максвелла
- Вычислимость и волновое уравнение
- Уравнение движения Лоренца; убегающие частицы
- Специальная теория относительности Эйнштейна и Пуанкаре
- Общая теория относительности Эйнштейна
- Релятивистская причинность и детерминизм
- Вычислимость в классической физике: где мы находимся?
- Масса, материя и реальность
- Специальная теория относительности Эйнштейна и Пуанкаре
- Зачем нужна квантовая теория гравитации?
- Нужна ли философам квантовая теория?
- Глава 1. Теория складского учета
- Теория
- 15.4.1. Базовая теория make
- Теория раскрутки
- Глава 1 ТЕОРИЯ И МЕТОДОЛОГИЯ РЕГИОНАЛЬНОГО БРЕНДИНГА
- 2.4. Теория налоговой привязки
- «Парадокс» Эйнштейна, Подольского и Розена
- Теория шести рукопожатий 2.0
- Глава 1 Кластеры, бенчмаркинг, стратегии: что дает теория конкуренции для понимания практики?




