Книга: Почему

Вероятности

Вероятности

Эта глава начиналась со строчки из рекламного объявления: «Получите образование, найдите работу и не заводите детей до брака – и 98 шансов из 100, что бедность вам не грозит!» Само утверждение – попытка вывести причинную зависимость: когда такие факторы, как высшее образование, работа и брак до рождения детей, считаются истинными, вероятность, что удастся избежать бедности, составляет 0,98. Эта статистика особо убедительна потому, что шансы очень близки к стопроцентным; и все же высокая вероятность не значит, что это соотношение каузально. Точно так же, как может иметь место сильная вероятностная зависимость, не носящая причинного характера, могут существовать и каузальные зависимости, когда причина снижает или не меняет вероятности наступления следствия вообще.

Так в чем же привлекательность вероятностных концепций причинности?

Как и в примере с радиоактивным распадом, одна из причин, по которой мы нуждаемся в вероятностных подходах (не требующих, чтобы причина всегда и безусловно производила следствие или каждый раз ему предшествовала), состоит в том, что некоторые отношения не детерминированы. В таких случаях при всем знании мы не можем быть убеждены, произойдет ли то или иное следствие. Здесь не только не будет закономерности в событиях, какую требуют все ранее описанные подходы, но также ни одна комбинация переменных не даст возможности ее установить.

Примеры индетерминизма часто встречаются в физике (например, в квантовой механике), а также в более приземленных ситуациях – скажем, при неисправности оборудования.

Но во многих других случаях, однако, вещи кажутся недетерминированными лишь в силу нехватки знаний – даже если их можно целиком спрогнозировать на основе полной информации. Не все, кто работает с асбестом, заболевают раком; лекарства дают побочный эффект только части пациентов; сходные условия не всегда приводят к образованию пузыря на фондовой бирже. Может, однако, случиться так, что, зная досконально действие лекарства или имея возможность пронаблюдать достаточно побочных эффектов и пациентов, у которых они обнаруживаются, можно выявить набор необходимых факторов.

Нам в основном приходится иметь дело не только с показателями наблюдений (нельзя заставить людей стать заядлыми курильщиками, чтобы посмотреть, кто из них заболеет раком), но еще и с неполными данными. Это означает, что мы упускаем некоторые переменные (вероятно, сведения по аэробной способности – лишь результаты оценки, а не измерения с помощью теста VO₂ max[201] на «бегущей дорожке»), можем наблюдать данные только на ограниченном временном отрезке (отслеживаем последствия хирургической операции 1 год, а не 30 лет) или берем пробы в режиме, далеком от идеального (отмечаем обмен веществ в тканях мозга раз в час вместо режима ЭЭГ). Проблема может заключаться в затратности (в масштабных исследованиях делать тесты VO₂ max неразумно с финансовой точки зрения, а также длительно по времени и потенциально небезопасно для больных людей), возможности сбора данных (редко есть шанс следить за человеком десятки лет) или технологических ограничениях (микродиализ[202] для измерения метаболизма – процесс медленный). Вероятностные подходы часто путают эти вероятности (одна – из-за недостатка знаний, другая – из-за природы самой зависимости), однако стоит помнить, что это разные вещи.

Один из главных мотивов использования вероятностных определений причинности – наше желание знать, служит ли нечто причиной и насколько важно это нечто. Иными словами, мы стремимся различать обычные и редкие побочные эффекты лекарственного средства или сформулировать политическую концепцию, которая вероятнее всего привела бы к росту рабочих мест. Один из методов, позволяющих квантифицировать степень влияния причины на следствие, – определить силу следствия, когда переменные непрерывны (например, как повышается цена акции после выпуска новостей), или вероятность некоего события, когда они дискретны (например, какова вероятность, что цена на акции пойдет вверх).

Но часто все, что удается вычитать в книгах на тему причинно-следственных взаимосвязей, это утверждение, что риск некоторого исхода увеличивается по некоторой причине. Вот несколько начальных строк из статей в научных изданиях:

Множество других статей начинается с упоминания о снижении или повышении риска, при этом точные цифры роста или падения даются несколькими абзацами ниже. И даже в этом случае данные, приведенные во всех подобных примерах, относительны: удвоить шансы или снизить риск на 50 %. Конечно, фраза «удвоить шансы на некое событие» может прозвучать совсем по-другому, однако, когда речь заходит о двух событиях вместо одного, все гораздо менее убедительно. Скажем, повышение риска инсульта у человека, иногда употребляющего алкоголь, составит либо 0,0000001–0,0000002, либо 0,1–0,2. В обоих случаях шансы удваиваются, но в первом удвоению подлежит очень маленькое число, и результирующее число также остается крайне малым.

На рис. 5.3 это различие представлено наглядно. Для набора из 10 000 000 событий самая низкая степень вероятности составит всего 1, а потом 2. Таким образом, для каждого отдельного события на рисунке есть обозначающие их точки, в то время как каждая из остальных точек на рисунке обозначает 10 000 событий. Итак, при том же удвоении относительного риска можно иначе решить вопрос с курением, когда станут видны абсолютные значения.

Рис. 5.3. Каждая точка представляет 10 000 событий, кроме нижних двух картинок, где черные точки обозначают единичные события. Вероятность событий, представленных черными точками, удваивается от левых картинок к правым, однако необходимо также принимать во внимание общее количество событий

Эту идею степени влияния причины на следствие, или количества вероятности, очень важно вспомнить позднее, при рассмотрении проведения и оценки экспериментов и формулирования политических концепций. Кроме того, постарайтесь держать ее в уме, когда будете в следующий раз читать о новейшем научном открытии.

Особо важно знать размер выборки (велика ли численность исследуемого населения), поскольку без значительного количества наблюдений мы не сможем даже дифференцировать эти результаты[206]. Различие может объясняться естественными вариациями, помехами или погрешностями измерений. К примеру, в зависимости от индивидуальных факторов риска, риск субарахноидального кровоизлияния – редкий, но часто приводящий к смерти вид геморрагического инсульта – составляет всего 8 на 100 000 человеко-лет[207]. Это значит, что если отслеживать 100 000 человек в течение года или 10 000 человек в течение 10 лет, можно ожидать, что мы увидим 8 случаев инсульта. Поэтому гораздо менее вероятно наблюдать истинные вероятностные показатели на меньших выборках: в результате эта цифра может составить 8 или 0 событий, что приведет к некорректным заключениям о степени риска.

Подобно тому как в центре юмовского подхода к причинности лежит регулярная повторяемость событий, идея вероятностной причинности основана на том, что причина повышает вероятность наступления следствия.

Если одно событие не имеет причинно-следственной связи с другим, вероятность второго не должна изменяться после того, как станет известно о первом. К примеру, вероятность выпадения орла или решки при подбрасывании монетки составляет ?, при этом вероятность того или другого исхода не меняется после первого броска, поскольку все события независимые. То есть вероятность выпадения орлов четко равна вероятности выпадения решек, если при предыдущем броске выпала решка.

Эта концепция представлена на рис. 5.4 (a) в виде эйкосограммы (также ее называют мозаичной диаграммой или диаграммой Маримекко[208]). По оси Х указаны возможные исходы первого события (орлы или решки), по оси У – исходы второго события (также орлы или решки). Ширина столбцов отражает вероятность выпадения орла или решки при первом броске (если монетка сильно несимметричная, первый столбец будет очень узким), а высота серых столбцов показывает вероятность выпадения орла при втором броске (оставшаяся область обозначает вероятность выпадения решки).

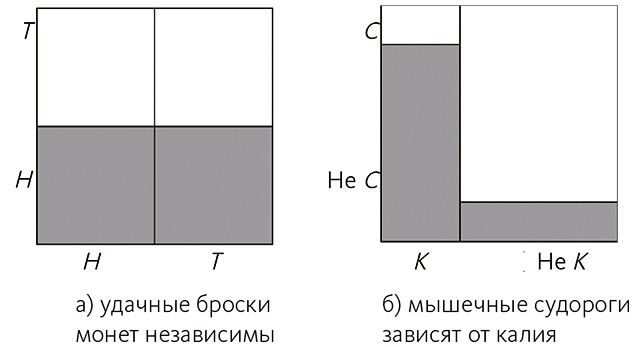
Рис. 5.4. На диаграммах представлены условные вероятности. Как только вы выбираете событие в нижней части (например, К), вероятность второго события (не С) обозначается закрашенным столбцом. С маловероятно после К (маленький столбец), в то время как орел или решка с равной степенью вероятности выпадают после любого броска (столбцы одинаковых размеров)[209]

Так как вероятность любого исхода абсолютно одинакова, все сегменты равны[210]. С другой стороны, вероятность того, что конкретного человека изберут кандидатом в вице-президенты, выше или ниже в зависимости от того, кто будет претендовать на президентский пост: тут важны политические убеждения и альянсы, так что эти события зависимы.

На интуитивном уровне, если нечто влечет за собой следствие, после появления причины следствие должно произойти с большей вероятностью, чем обычно. То есть в местностях, где обитают малярийные комары, должно отмечаться больше случаев заболевания, так как комары – разносчики инфекции. Причина также может снизить вероятность следствия – если точнее, причина повышает вероятность отсутствия его наличия. Так, если калий успокаивает мышечные судороги, мы должны отмечать меньше подобных случаев после принятия препаратов калия. Этот случай показан на рис. 5.4 (б), когда вероятность потребления калия (К) ниже, чем непотребления, так что соответствующий столбец уже. Однако большая часть столбца закрашена, поскольку шанс отсутствия мышечных судорог (нет С) намного выше, чем шанс судорог при принятии калия. И наоборот, возможность начала судорог без добавления в организм калия намного выше.

Это простая идея повышения или снижения вероятностей способна привести одновременно как к ложным утверждениям о причинности (поскольку может показаться, что непричины усиливают вероятность следствий), так и к невозможности эту связь выявить (так как не каждая причина увеличивает вероятность следствия).

В главе 3 мы познакомились с корреляциями и порядком их возникновения. В некоторых ситуациях они оказываются результатом простого совпадения, в других же можно протестировать так много гипотез, что рано или поздно совершенно случайно проявится нечто значительное.

Еще может случиться так, что используемые переменные не будут точно представлять фактические причины. К примеру, о диете скажут, что она обеспечивает определенный уровень похудения, однако соответствующей переменной, вызывающей потерю веса, может стать следование любой диете, а не той конкретной, которую мы тестируем. Возможно также, если мы просто рассмотрим зависимость двух факторов, обнаружится множество аналогичных закономерностей вследствие неких структурных условий. В главе 3 мы видели выявление ложной корреляции между потреблением шоколада в стране и количеством Нобелевских лауреатов среди ее жителей. Возможно, повышенные объемы вина, сыра или кофе имели бы не менее сильные ассоциации с Нобелевками. Действительно, согласно одному исследованию, среди прочего наблюдалась взаимосвязь между числом Нобелевских премий и количеством магазинов IKEA[211]. Таким образом, потребление шоколада могло быть аналогом некоего индикатора населения, который повышает вероятность одновременного поедания этого продукта и получения Нобелевки, например благосостояния и ресурсов страны.

Именно на подобный тип общей причины нередко возлагают вину, когда одна переменная, кажется, делает другую более вероятной, но в действительности ее причиной не служит. К примеру, если рецессия приводит одновременно к снижению инфляции и безработице, можно решить, что каждый из этих факторов повышает шансы на проявление другого. Мы просто берем пары переменных и интересуемся, усиливает ли одна из них вероятность другой.

Есть и такая методика работы со смешиванием эффектов из-за общих причин (когда измеряются все переменные) – выяснить, можно ли с помощью одной переменной оправдать корреляции между другими. Это ключевой атрибут множества вероятностных подходов, разработанных философами (такими как Саппс (1970), Гуд (1961) и Рейхенбах (1956)), на котором построены вычислительные методы выведения причин по имеющимся данным.

Скажем, некое заболевание (D) вызывает утомляемость (F) и обычно лечится определенным лекарством (М). Идея в том, что смена препарата не приведет к улучшению состояния пациента (утомляемости), если проблема вызвана только болезнью и не решается лекарством. Если заболевание остается константой, другие переменные не дают никакой информации друг о друге. Концепция общей причины, которая подобным образом разделяет следствия, называется экранированием[212].

Обратимся к диаграмме на рис. 5.5 (а). Есть лекарство, и есть усталость; похоже, первое повышает вероятность второй. Серый столбец выше для усталости, чем для неусталости, показывая, что вероятность выше для случая, когда лекарство истинно, чем ложно. Но как только мы разделим варианты, когда человек болен и когда нет (рис. 5.5 (б) и 5.5 (в)), вероятность усталости уравнивается, вне зависимости от значения препарата. Таким образом, лечение не меняет возможность усталости, как только мы получаем знание о болезни.

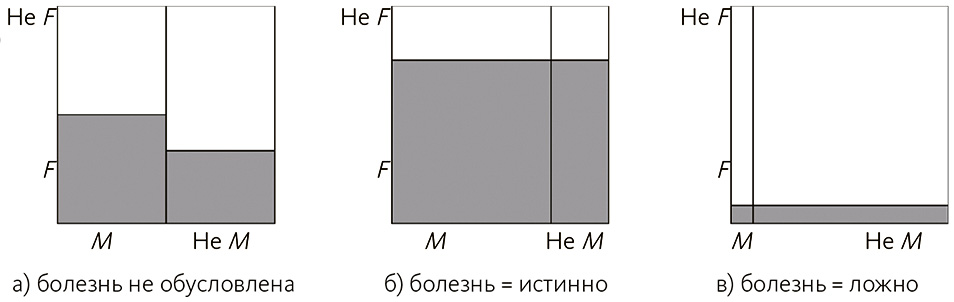
Рис. 5.5. Если не принимать во внимание состояние заболевания, кажется, что M и F коррелируют. Если, однако, учитывать этот фактор, корреляции нет (F равновероятен независимо от истинности М)

Подобный тип разделения также может иметь место в цепи событий. Скажем, болезнь приводит к назначению лекарства, и здесь оно действительно вызывает усталость как побочный эффект. Если отношения D ? M и M ? F истинны, мы также обнаружим, что болезнь повышает вероятность усталости. Однако часто требуется выявить самые непосредственные причинные взаимосвязи, чтобы осуществить более прямые вмешательства. Чтобы избежать появления симптома, нужно отменить лекарство или перейти на другое; но, если мы придем к ошибочному заключению, что как болезнь, так и лекарство провоцируют усталость, мы не сможем узнать, что смена препарата могла бы предотвратить возникновение симптома. И снова, если мы ставим условием М, вероятностное отношение между D и F исчезает.

Как обычно, ни один метод не совершенен, и успех зависит на самом деле от измерения общей причины. То есть, если рецессия приводит одновременно к снижению инфляции и безработице и мы не знаем, имеет ли место рецессия, нет возможности использовать условие экранирования, чтобы выяснить, не ложна ли видимая причинная зависимость между инфляцией и безработицей. Получается, реальные мы найдем взаимосвязи или ошибочные, целиком зависит от наличия верного набора переменных.

Эта проблема вновь выйдет на передний план, когда в главе 6 мы затронем вычислительные методы. Но, хотя на базе ряда сценариев мы и располагаем несколькими способами отыскать скрытую общую причину, это не решает проблему вычислительных методов в целом.

На этом, однако, история не заканчивается. Иногда просто нет единственной переменной для экранирования двух следствий. Скажем, Алиса и Боб любят занятия по машинному обучению[213] и предпочитают те, которые назначены на послеобеденное время. Тогда, взяв условием либо содержание курса, либо время, мы не сможем полностью экранировать такие переменные, как выбор занятий Алисой и Бобом. Если известно только время занятий, то запишется на них Боб или нет, действительно дает информацию о выборе Алисы, так как этот фактор становится косвенным индикатором содержания курса. Нет единственной переменной, экранирующей А и Б друг от друга.

И если мы добавим переменную, которая будет истинной, только если курс одновременно и начинается после полудня, и посвящен машинному обучению, этот фокус поможет. Но, чтобы понять необходимость этой более сложной переменной, нужно знать кое-что о проблеме и потенциальных причинных взаимосвязях, а это не всегда возможно.

Пока мы вообще не затрагивали временные паттерны (приняли как данность, что причина происходит до следствия). Однако иногда используется фактор, способный объяснить корреляцию, который мы обычно не включаем в свой анализ, – изменение взаимозависимости во времени.

Чтобы представить ситуацию, когда экранирование не срабатывает, вспомним примеры индетерминизма из начала этой главы. Если некое оборудование неисправно, это может помешать идеальному экранированию его эффектов. Чтобы это проиллюстрировать, часто используется пример с неисправным тумблером, одновременно включающим телевизор и лампу (он не всегда замыкает цепь). Если телевизор работает, горит и лампа, и наоборот, но, бывает, оба прибора не активированы. Для решения этой проблемы можно добавить четвертую переменную – замкнутую цепь; но, чтобы узнать о ее необходимости, нужно иметь некоторое понимание о структуре проблемы, а оно есть не всегда.

Один из вариантов – не рассматривать точную взаимосвязь, но изучить, будет ли возможная причина иметь большое значение для следствия, если другие факторы останутся неизменными. До сих пор мы анализировали все ситуации, при которых то, что нельзя считать причиной, может все-таки повышать вероятность следствия; но возможно также, что истинная причина не повысит эту вероятность. Один из очевидных примеров – это причина, предотвращающая следствие (например, вакцина, которая предупреждает болезнь). С такими случаями разобраться легко, поскольку мы можем либо переопределить факторы в терминах снижения вероятности, либо применить отрицание следствия как интересующий нас исход (то есть «неболезнь»). Но как насчет иных ситуаций, когда положительная причина снижает вероятность или вообще не оказывает никакого действия? Здесь ключевые факторы – это выборка, на основе которой берется информация, и степень детализации переменных.

Оглавление книги