Книга: Почему

Парадокс Симпсона

Парадокс Симпсона

Представим, что вы пациент, которому надо выбрать одного из двух врачей. У доктора А (Алиса) смертность пациентов, проходивших лечение от определенной болезни, составляет 40 %, у доктора B (Бетти) – 10 %. Если исходить только из этой информации, легко выбрать Бетти; на самом деле у вас недостаточно данных, чтобы принять подобное решение.

Действительно, возможно, что для каждого отдельного пациента лечение у Алисы дает лучшие результаты, даже если кажется, что общий уровень смертности у нее выше.

Алиса и Бетти не выбирают пациентов случайным образом: видимо, их направляют другие врачи, или те приходят по объявлениям. Поэтому, если большой опыт Алисы привлекает к ней самые сложные и трудноизлечимые случаи, общий уровень смертности может показаться очень плохим, хотя как доктор она и лучше.

В этом примере интересно то, что мы не просто обнаруживаем ошибочную причинную зависимость, но и можем реально выявить зависимость, обратную истинной: что результаты Алисы хуже, хотя в действительности они лучше. Точно такой же сценарий может иметь место с медикаментами, если не анализировать данные выборочных экспериментов (когда пациенты распределяются по группам лечения случайным образом).

Главная проблема в том, что может быть смещение относительно того, кто какое лекарство принимает, а устранить его на деле получится только выборочным распределением пациентов по группам. К примеру, если больные с агрессивной формой рака получают лечение А, а с более легкими случаями – лечение В, несомненно, результаты А покажутся хуже, поскольку эта группа имеет более серьезные проблемы. Смещение выборки – одна из причин, по которой так сложно делать логические заключения на основе данных наблюдения. Можно обнаружить, что люди, активно занимающиеся спортом в пожилом возрасте, живут дольше тех, кто ведет малоподвижный образ жизни, – но, возможно, потому, что физически активные всю жизнь просто здоровее прочих.

Странный феномен, когда причинные взаимосвязи исчезают или обращаются вспять, известен как парадокс Симпсона[214], [215]. Симпсон описал математические свойства, которые должны быть присущи данным, чтобы такая ситуация смогла возникнуть. Он привел пример, когда лечение приносит пользу, если данные по пациентам разного пола рассматриваются отдельно, но кажется неэффективным для контингента в целом. Другие исследователи показали, как возникает еще более экстремальная ситуация, когда новое лечение на деле приводит к повышению смертности у населения в целом, хотя и мне, и еще кому-то оно помогло[216]. Это показано на рис. 5.6. Прочие известные примеры – процент поступивших в Беркли (когда показатель для женщин кажется ниже, поскольку они подают документы на факультеты с высоким конкурсом)[217] и количество смертных приговоров во Флориде (когда казалось, что раса подсудимого влияла на приговор, хотя в действительности на него влияла раса жертвы)[218].

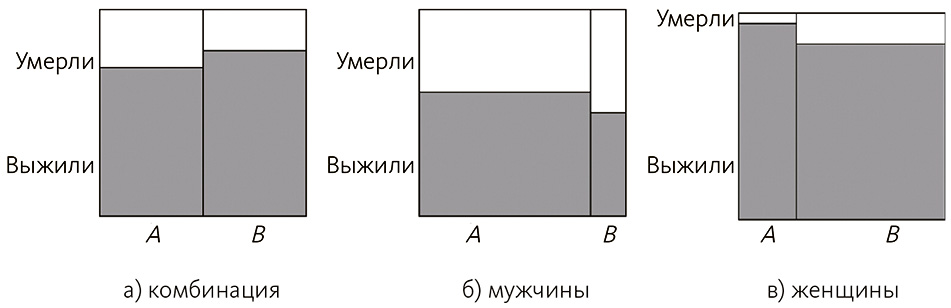
Рис. 5.6. Иллюстрация парадокса Симпсона, где А лучше в каждой подгруппе, но В кажется лучше в комбинации

В каждом из примеров парадокса Симпсона можно объяснить сомнительную взаимосвязь с новой информацией – особенно если рассматривать подгруппы. В примере с докторами, изучив группы пациентов с одинаковым состоянием здоровья или уровнем риска, можно сделать вывод, что показатели Алисы лучше. В примере с процентом поступивших в Беркли можно провести стратификацию по факультетам, а в примере со смертными приговорами – по расовой принадлежности жертв. Это значит, что все дело в уровне детализации при изучении данных. Чтобы вывести на основе данных вероятностные зависимости, нужно знать, что наблюдаемые вероятности репрезентативны для зависимостей, лежащих в их основе. Если наша задача – осуществление политической программы, необходимо знать, что вероятности для одной группы населения применимы ко всей целевой группе.

Конечно, ключевая проблема – определить, когда и как подразделить имеющиеся данные, поскольку неверно, что очередное дробление решит вопрос. Можно иметь контринтуитивные результаты для отдельной подгруппы, которые не получить на агрегированных данных, и более мелкое деление снова изменит взаимосвязи. В примере с лекарством, лучше действующим на мужчин и женщин в индивидуальном порядке и хуже – на все население, вероятно, мы должны поверить, что лекарство вообще работает. Хотя подобная точка зрения немало дискутировалась, сам Симпсон считает, что такое лечение «вряд ли можно отвергать как бесполезное для всей человеческой расы, если оно приносит пользу мужчинам и женщинам»[219]. И все же он приводит пример, когда подобная интерпретация оказывается несостоятельной. Корректный набор переменных, используемых как условия, можно найти, однако для этого требуется, чтобы мы уже имели некоторое знание о причинно-следственной структуре. А это проблематично, если мы только приступаем к ее изучению[220].

Именно здесь кроется корень многих вопросов причинности. Мы просто не в состоянии полностью устранить потребность в базовом знании проблемы и обязаны использовать это знание, чтобы выбирать данные для анализа и интерпретировать результаты.

Оглавление книги