Книга: Как спроектировать современный сайт

Математические формулы

Математические формулы

Кирпичи просто создавать, использовать, они понятны и просты, но на протяжении столетий возникло и сформировалось более тонкое понимание систем упорядочения. Эти открытия и нововведения развивали наше понимание сеток. Обращаясь к математике, природе и даже к собственному телу, мы веками пытались выявить скрытую в мире логику и порядок.

В VI веке до н. э. греческий философ Пифагор сформулировал теорему, ныне известную как теорема Пифагора, – математическую модель, описывающую три стороны треугольника. Эта теорема стала концептуальной основой геометрии, которую изучают студенты-математики, даже не осознавая, почему это необходимо. Теорема Пифагора наглядно показывает, что взаимоотношения между простыми числами предполагают внутренний порядок. Так что на самом деле Пифагор поднял значение математики, превратив ее в философскую основу постижения мира.

Пифагор считается одним из первых математиков, определивших золотое отношение (1:1,618), описывающее гармоничную взаимосвязь двух чисел. Это отношение часто называют золотым сечением, а его особенности долгое время занимали умы величайших математиков. Золотое сечение служило источником вдохновения для художников и архитекторов с древних времен. Эстетический эффект, который возникал при взгляде на сооружения или картины, в основе которых лежал принцип золотого сечения, производил неизгладимое впечатление. Неслучайно мы замечаем, что этот принцип был использован во многих шедеврах мировой культуры.

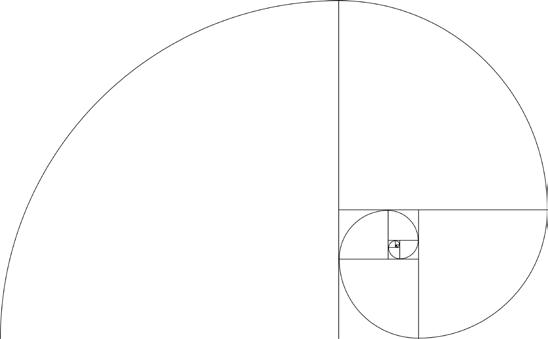
Спираль Фибоначчи образует сетку, используемую человечеством на протяжении столетий

Золотое отношение непосредственно связано с одной интересной математической концепцией – последовательностью Фибоначчи. Она была известна с древнейших времен и использовалось древнеиндийскими учеными еще в 200 году до н. э., но получила свое название в честь итальянского математика, жившего в эпоху Возрождения.

Последовательность Фибоначчи представляет собой ряд чисел, начинающийся с нуля и единицы. Каждое последующее число равно сумме двух предыдущих, таким образом первые числа последовательности образуют следующий ряд:

В результате деления любого числа из последовательности Фибоначчи на предыдущее получается очень близкое к золотому отношению значение —1,618 (иногда больше, иногда меньше). Для больших чисел результат будет стремиться к 1,618.

Для дизайнеров важнее всего знать, что последовательность Фибоначчи, отображенная в виде логарифмической спирали, является основой сетки, которую принято считать самой гармоничной и логичной.

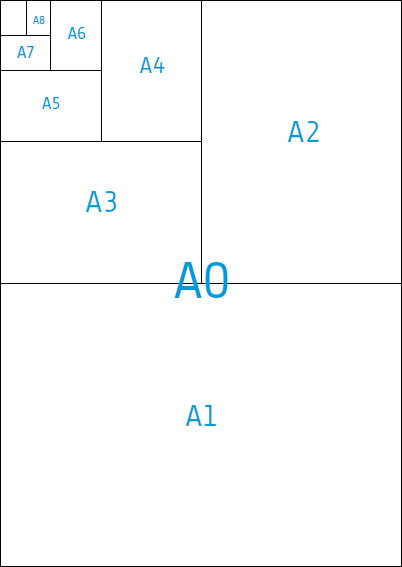
Используемый во всем мире стандарт ISO 216, описывающий бумажные форматы, основан на прямоугольнике с соотношением сторон, равным квадратному корню из двух

Аналогичную сетку можно построить на основе прямоугольника с соотношением сторон, равным квадратному корню из двух (его иногда путают с золотым прямоугольником). При делении пополам данный прямоугольник сохраняет то же соотношение сторон. Это особенно важно для дизайнеров, ведь такие прямоугольники стали базой международных стандартов на размеры бумаги (ISO 216, в основе которого лежит немецкий стандарт DIN 476). Данный стандарт широко используется в Европе и некоторых других странах, но не в США и Канаде. Он принят Организацией Объединенных Наций как официальный формат. Такой единообразный подход к производству, реализации и использованию бумаги оказал заметное влияние на работу графических дизайнеров во множестве стран, использующих международный стандарт, потому что он предоставил основу, на которую можно опираться при создании новых проектов.

Чуть менее обоснованным считается так называемое правило третей, которое, по сути, правилом не является и слабо связано с математикой. Появившийся в XVII веке упрощенный метод широко используется художниками, графиками, фотографами и дизайнерами (в меньшей степени архитекторами) для создания гармоничной композиции. Правило гласит, что эффективную композицию можно получить, разделив изображение натри столбца одинаковой ширины и три строки одинаковой высоты. На пересечении разделительных линий образуются четыре точки, на которых концентрируется внимание человека. Из правила третей следует, что за счет выравнивания элементов относительно этих разделительных линий или при размещении элементов в центральных точках можно сфокусировать внимание, вызвать максимальный интерес, передать энергию или напряжение.

Возможно, из-за своей простоты правило третей является наиболее полезной из многочисленных «формул», описывающих эстетическую целесообразность. Ее простота убедительна, а деление на равные трети легко запомнить. Это особенно заметно, если сравнить данный метод с более сложными вариантами, рассмотренными ранее. Золотое отношение, последовательность Фибоначчи, да и другие математические исследования оказали неоспоримое влияние на теорию сеток, но в большинстве обычных ситуаций их используют существенно реже, чем методы попроще.

К счастью, золотое отношение, наиболее важное для дизайнеров, не требует дополнительного изучения. В примерах, приведенных в данной книге, вы найдете множество практических рекомендаций по его повседневному применению. Основной подход прост – чем более простой метод используется для создания сетки, тем более эффективной будет ее организация.

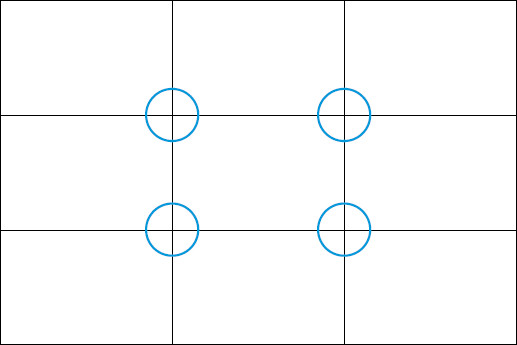
Правило третей позволяет определить четыре центральные точки в любой композиции, на которых естественным образом концентрируется внимание человека

Оглавление книги