Книга: Программирование игр и головоломок
5. Стратегия без игры (выигрывающие стратегии)
5. Стратегия без игры (выигрывающие стратегии)
Игра 27.
Рассмотрим игру НАДЕВАТЬ. В начале на игровом поле ничего нет. Можно играть только на поле, которое следует эа первым занятым полем, а такого поля нет. Играем на поле 1.
На следующем ходе было бы глупо снимать только что выставленную шашку. Первое занятое поле — первое. Ставим шашку на поле 2. Первое занятое поле — это снова первое поле. Было бы глупо снимать только что выставленную шашку, и поэтому нужно играть на первом поле, т. е. освобождать его. Теперь первое свободное поле — это поле 2. Было бы глупо возвращать на поле 1 только что снятую шашку. Следовательно, поставим шашку на поле 3. Никакого выбора…
Чтобы освободить игру на одно поле, очищаем поле 1.
Чтобы освободить игру на два поля, мы не можем очистить поле 1, так как тогда мы не могли бы очистить и поле 2. Первое занятое поле — поле 1. Можно очистить поле 2, а затем поле 1.
Для игры с 3 полями, мы очищаем 1, эатем ставим 3, ставим снова 1, очищаем 2, а затем 1.
Если n четно, то мы начинаем с удаления шашки 2, в противном случае мы удаляем шашку 1.
Теперь вам не составит ни малейшего труда написать итеративную программу:
место := 0; игра : = пусто
ВЫПОЛНЯТЬ
ЕСЛИ поле (1) = пусто ТО поставить (1);
место := место + 1
ИНАЧЕ удалить (1);
место := место ? 1
КОНЕЦ_ЕСЛИ
ЕСЛИ место = n ТО КОНЧЕНО КОНЕЦ_ЕСЛИ
искать первое занятое поле, номер которого дает число i;
ЕСЛИ поле (i + 1) = пусто ТО поставить (i + 1);
место := место + 1
ИНАЧЕ удалить (i + 1);
место := место ? 1
КОНЕЦ_ЕСЛИ
ЕСЛИ место = n ТО КОНЧЕНО КОНЕЦ_ЕСЛИ
ВЕРНУТЬСЯ
Для игры СНИМАТЬ вы действуете аналогично.
В том, что касается последовательностей чисел, порожденных игрой СНИМАТЬ, начнем с рассмотрения конкретного примера. Вот игра СНИМАТЬ для n = 4.
| 0001 | 1 |
| 0011 | 3 |
| 0010 | 2 |
| 0110 | 6 |
| 0111 | 7 |
| 0101 | 5 |
| 0100 | 4 |
| 1100 | 12 |
| 1101 | 13 |
| 1111 | 15 |
Использованы все числа, меньшие 8, а из больших или равных 8 участвуют только 12, 13 и 15. Для обобщения действуйте по индукции.
Игра 29.
Вот решение для 8 букв и 10 полей.
..абабабаб
баабаба..б
бааб..аабб
б..баааабб
ббббаааа..
Присутствие куска X не меняет последовательности изменений.
..абабХабаб
баабабХа..б
бааб..Хаабб
б..бааХаабб
ббббааХаа..
Последний перенос пары букв аа слева от X в свободные пары справа дает
бббб..Хаааа
Теперь вы можете заняться X (если для этой комбинации вам решение уже известно) и получить
ббббY ..аааа
Таким образом, остается переместить два а с крайних полей справа на свободные поля, и все закончено. Следовательно, если вы умеете исследовать комбинацию Х с р парами букв а, б, то вы умеете исследовать и комбинацию с р + 4 парами.
Я уже предложил вам решение для четырех пар. Таким образом вы получаете решение для 8, 12,…
Главные решения — это решения для 4, 5, 6, 7 пар. Вот одно из решений для строчки из 5 пар
..абабабабаб
Искомое расположение имеет вид
бббббааааа..
Можно задаться целью удалить все буквы а (особенную трудность при перемещениях вызывает то, что их число нечетно) из первой половины (первых 5 позиций, в которых букв а в исходном положении не столько же, сколько букв б).
..абабабабаб
баабабаба..б
бааб..абаабб
бааббаа..абб
б..ббааааабб
бббббааааа..
Предлагаю вам разыграть 6 и 7 пар. Совершенно бесполезно подключать к этому делу компьютер. А где же программирование, спросите вы? Я отвечу, что это упражнение вводит вас в рекурсивные или индуктивные рассуждения. Это оздоровляет Наши способы рассуждать…
Игра 30.
Единственная настоящая задача, если вы работаете итеративным способом — организовать испытания так, чтобы иметь возможность совершенно систематически проводить их и обновлять игру, сохраняя список ходов, чтобы иметь возможность вернуться назад.
Игра имеет ту же конфигурацию, что и для лис и кур. Поле обозначается своим положением в цепочке. Перемещение в данном направлении реализуется добавлением некоторой константы к данному положению. Таблица из четырех элементов дает эти константы для всех четырех направлений. Свободное поле представляется точкой, занятое поле — крестиком ?.
Вы ищете первый крестик в цепочке и вы начинаете с первого возможного перемещения i = 1. Если есть возможность взятия в этом направлении, то вы регистрируете данные ?, i в цепочке или таблице (во втором случае вы симулируете кучу). Вы выполняете взятие и начинаете сначала. Если же возможности взятия в данном направлении нет, то вы переходите к следующему i. Если вы достигаете четырех, то с этим крестиком все кончено, и вы переходите к следующему. Если их больше нет, то вы возвращаетесь к последней зарегистрированной в куче паре данных ?, i, отменяете соответствующее взятие (изменение состояния игры) и продолжаете переходом к следующему i.
Вы уже проделали более трудную работу для самого длинного взятия в игре с курами и лисами.
Игра 31.
Число ходов f(р) для переноса р дисков получается переносом сначала p ? 1 дисков со стержня d на стержень 3 ? а ? d за f(р ? 1) ход, затем из перемещения диска р, что требует в точности одного хода, а затем возвращения р ? 1 дисков из запаса на стержень прибытия за f(р ? 1) ход, откуда получаем:
f(р) = 2 * f(р ? 1) + 1,
g(p) = f(p) + 1 = 2 * f(р ? 1) + 2 = 2 * (f(p ? 1) + 1) ? 2 * g(р ? 1).
По индукции g(р) = 2pg(0).
Так как f(0) = 0, g(0) = f(0) + 1 = 1, g(р) = 2p, то, наконец
f(р) = 2p ? 1.
Для игры с 50 дисками нужно 250 ? 1 ходов. Но 210 равно 1024, или порядка 103. Следовательно, 250 порядка 1015.
В часе 3600 секунд, в сутках 3600 ? 24 = 86400 секунд, за год получаем 86400 ? 365 — или порядка 3 ? 107 секунд, откуда, наконец, 3 ? 109 секунд за столетие. Поэтому нужно порядка 1015/3 ? 109, или порядка 3 ? 105 веков для игры с 50 дисками, которая, таким образом, требует около 300000 веков…
Вот другой способ доказывать свойство четности. Пусть диски обозначены их порядковыми номерами, начиная с первого — самого маленького, и нужно показать, что два диска с номерами одной четности никогда не попадают непосредственно один на другой.
Опыт показывает, что для первых значений n реализация игры Н(n, d, а) дает следующее;
— диски, попадающие в основание стержней d и а, имеют ту же четность, что и n,
— диски, попадающие в основание запасного стержня, имеют другую четность.
Предположим, что это свойство справедливо для n ? 1. Для реализации Н(n, d, а) нужно выполнить сначала Н(n ? 1, d, 3 ? а ? d). В течение этой операции диск n остается в основании начального стержня d и, следовательно, в основании диска d находится диск n и потому диск той же четности, что и n. Диски, которые при этом оказываются в основании стержня прибытия для процедуры Н(n ? 1, d, 3 ? а ? d), имеют (по предположению индукции) ту же четность, что и n ? 1. Но этот стержень прибытия является для игры Н(n, d, а) запасным стержнем, и, следовательно, в основании запасного стержня оказываются диски, имеющие ту же четность, что и n ? 1. Наконец, запасной стержень для игры Н(n ? 1, d, 3 ? а ? d) есть а, в основание которого попадают диски с четностью n ? 2, следовательно, с четностью n.
Перемещение диска n со стержня d на стержень а помещает n в основание стержня а, так что при этом свойство четности для а подтверждается. Проверьте, что для стержней d и 3 ? а ? d оно также подтверждается. Для этого разложите Н (n, d, а) на 5 операций:
Н (n ? 2, d, а) n и n ? 1 на стержне d
Р (n ? 1, d, 3 ? а ? d) n на d, n ? 1 на 3 ? а ? d
Н (n ? 2, а, 3 ? а ? d)
Р (n, d, а) n на а, n ? 1 на 3 ? а ? d
Н (n ? 2, 3 ? a ? d, d)
Р (n ? 1, 3 ? а ? d, а) n на а, n ? 1 на а
Н (n ? 2, d, а).
Предположим, что искомое свойство четности выполняется для n ? 1. Тогда остается заниматься только теми дисками, которые ложатся на диск n.
В первой операции диск n ? 1 находится на диске n, они разной четности, и, таким образом, здесь свойство четности выполняется. Во время игры Н(n ? 2, а, 3 ? а ? d) диск n находится на стержне, который для этой игры является запасным. Диски, которые в этой игре ложатся в основание этого стержня — и потому ложатся на диск n — имеют четность, противоположную четности числа n ? 2, следовательно, четность, противоположную четности n, что и проверяет на этом этапе наше условие четности. Вы легко завершите это рассуждение.
Разобранный пример хорошо иллюстрирует тесную связь между рекурсивностью и рекуррентностью, которые представляют собою не что иное, как две немного отличающиеся реализации одного и того же рассуждения.
Игра 33.
Предположите, что в Н (n ? 1, d, а) диск 1 перемещается всегда в одном и том же направлении. Для Н (n, d, а) вы должны выполнить
Н (n ? 1, d, 3 ? а ? d)
Н (n ? 1, 3 ? а ? d, а).
Вместо того, чтобы непосредственно переходить от d к а, вы осуществляете этот переход с помощью стержня 3 ? а ? d, иначе говоря, вы делаете два перемещения в обратном направлении. Диск 1 продолжает перемещаться всегда в одном и том же направлении, но это направление меняется при переходе от n ? 1 к n. Для n = 1 этот диск перемещается в направлении от d к а. Это всегда будет так для всех нечетных n, в то время как для четных n он будет перемещаться в направлении от а к d.
Простое итеративное решение имеет следующий вид: исходя ив четности n определите направление перемещения диска 1. Начните с 2n ? 1 число ходов, которые осталось сделать:
s := ЕСЛИ четно (n) ТО 2 ИНАЧЕ 1 КОНЕЦ_ЕСЛИ
d := 0; k:= 2n ? 1
ВЫПОЛНЯТЬ
а := d + s; ЕСЛИ a > 2 ТО а := а ? 8
КОНЕЦ_ЕСЛИ
переместить диск 1 с d на а;
d : = a; k := k ? 1
ЕСЛИ k = 0 TO КОНЧЕНО КОНЕЦ_ЕСЛИ
переместить единственный диск, который можно переместить, кроме диска 1
k := k ? 1
ВЕРНУТЬСЯ
Все диски имеют общее свойство: нечетные диски перемещаются в том же направлении, что и диск 1, а четные диски — в другом направлении.
В вышеприведенной программе стратегия совершенна с точки зрения исполнения вручную, потому что в каждый данный момент сразу видно, какой диск нужно переместить, если это не самый маленький диск (меньший из двух остальных дисков перемещается на больший). В нашей программе вам нужно вычислить это движение. Один из наиболее простых способов состоит в том, чтобы представить игру с помощью вектора, дающего для диска i номер стержня, на котором он находится. Диск, подлежащий перемещению — это наименьший Диск, который находится не на том же стержне, что и диск 1, следовательно, номер стержня которого отличается от d. Этот самый диск перемещается со стержня, на котором он находится — с номером x — на стержень 3 ? x ? d.
Обозначим первое перемещение через 1. Поскольку диск 1 перемещается один раз в каждой паре ходов (точнее, перемещается через ход), то он перемещается в каждый нечетный ход. По индукции покажите, что диск p перемещается в ходы с номерами, которые делятся на 2р?1, но не делятся на 2p (т. е. являются нечетными кратными числа 2p?1).
Номер k любого хода может быть единственным способом представлен в виде
k = (2r + 1)2р-1.
Перемещаемый на этом ходе диск есть диск с номером p, и это — его (r + 1)-е перемещение. Так как он начинает движение со стержня 0 и перемещается в направлении sp (1, если р нечетно, и 2 в противном случае), то на этом ходе диск перемещается с rsp-го на (r + 1)sр-й стержень, где эти числа берутся по модулю 3.
Игра 34.
Попытаемся охарактеризовать значение р, дающее игре оптимум для данного n. Нам известно, что f3(n ? p)= 2n-p ? 1.
Должно выполняться
2f4(p ? 1) + 2n-p+1 ? 1 ? 2f4(р) + 2n-p ? 1,
2f4(p + 1) + 2n-p-1 ? 1 ? 2f4(р) + 2n-p ? 1.
Удобно пользоваться первыми разностями для функции f4:
d(р) = f4(p + 1) ? f4(p).
Два приведенных выше соотношения могут быть переписаны следующим образом:
d(p ? 1) < 2n-p-1, d(р) ? 2n-p-2.
Интересно рассматривать даже не d(р), а скорее 2pd(р) = g(р):
g(р ? 1) ~ 2n-2 ? g(р).
Можно еще упростить запись, беря не g(р), а величину
h(р) = log2(g(р)) = р + Iog2(d(р)).
Тогда получаем
h(р ? 1) < n ? 1 ? h(р).
При данном n величина р — наименьшее целое, для которого h больше или равно n ? 2.
Приведем здесь первые из полученных таким образом значений:
| n | q | f4 | p | d | h |
| 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 2 | 2 | |
| 2 | 3 | 2 | 3 | ||
| 3 | 2 | 5 | 1 | 4 | 5 |
| 4 | 9 | 1 | 4 | 6 | |
| 5 | 13 | 1 | 4 | 7 | |
| 6 | 3 | 17 | 3 | 8 | 9 |
| 7 | 25 | 3 | 8 | 10 | |
| 8 | 33 | 4 | 8 | 11 | |
| 9 | 41 | 5 | 8 | 12 | |
| 10 | 4 | 49 | 6 | 16 | 14 |
| 11 | 65 | 6 | 16 | 15 |
Мы добавили в таблицу переменное q, связанное с «треугольными» числами. Для n = q(q + 1)/2 действительно убеждаемся, что
h(р) = h(р ? 1) + 2
в то время как для других n
h(p) = h(p ? 1) + 1.
Исходя из n, можно вычислить q:
q = целая_часть ((
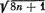
Имеем
h(n) = n + целая_часть ((
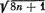
Покажите это по индукции. Исходя отсюда, вычисляется все. Таким образом, если n дано, то р — наименьшее целое, большее или равное
(2n ? 1 ?
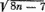
Игра 35.
Возьмем, например, игру с 50 дисками. Она реализуется переносом сначала 40 дисков на запасной стержень, а затем 10 последних дисков со стержня 0 на стержень 1, с использованием при этом только трех свободных стержней. Наконец, остается перенести начальные 40 самых маленьких дисков с запасного стержня на первый стержень, используя все 4 стержня.
Чтобы переместить 40 дисков с 4 стержнями, сводим задачу к перемещению 31 диска с 4 стержнями, а затем 9 с 3 стержнями…
Таким образом, дело сводится к разбиению 50 дисков на 8 сегментов:

Каждый сегмент перемещается с использованием 3 стержней, в чем мы следуем итеративной стратегии, которая уже описана выше. Единственный вопрос — это правильный выбор запасных стержней.
Договоримся работать с тремя стержнями 0, 1, 2, так что стержень 3 остается пустым и служит запасным стержнем при любом перемещении какого-либо сегмента. Более точно, перемещение сегмента р со стержня d на стержень а осуществляется с помощью изученной выше процедуры Н, в которой запасным стержнем является стержень 3.
Сегмент 1 перемещается в каждый из двух ходов подряд (под ходом я понимаю последовательность операций, реализующих процедуру Н), всегда в одном и том же направлении.
Мы сохраняем предыдущую итеративную стратегию, но понимаем ее как стратегию для сегментов. На компьютере это может пройти очень быстро. Вполне вероятно, что робот может осуществить одно перемещение за несколько секунд. Тогда на всю игру потребуется не более чем несколько часов…
Игра 36.
Соотношение SG (p, q) = 0 означает, что вы не можете достичь ситуации с числом Спрага-Грюнди, равным нулю, удаляя не более 2q спичек из кучки с р спичками. Если вы исходите из SG (р, q' < q), то вы не можете удалить столько же спичек и, следовательно, нет опасности, что вы получите число SG, равное нулю.
Предположим, что SG (pi, 1) = 0.
Исходя из pi + 1, я могу удалить 1 спичку и получить пару pi, 1. Следовательно, SG (pi + 1, q) ? 0.
Исходя из pi + 2, я для любого q всегда могу удалить две спички, но тогда я получаю SG (pi, 2) ? 0, и, следовательно,
SG (pi + 2, 1) = 0.
Если в pi имеем qi > 1, то тогда мы этого не получим и SG (pi + 2, 1) ? 0. Но в pi + 3, удаляя единственную спичку, получаем пару pi + 2, 1 c SG ? 0, или же, удаляя две спички, получаем пару pi + 1, 2 с ненулевым числом SG. Следовательно, SG (pi + 3, 1) = 0.
Все оставшееся уже очень хорошо подготовлено. Рассмотрите точку р, для которой диагональ пересекает ось р = 0, не пересекая положений с нулевым SG. Эта прямая задается уравнением x + у = р. Она пересекает ось x = 0 в точке у = р. Нельзя взять в точности р спичек, — можно не больше р ? 1. Следовательно, в этой точке
q = целая_часть ((р ? 1)/2).
Рассмотрим теперь точку, абсцисса которой есть число Фибоначчи: р = fib (s).
Нужно показать, что прямая x + у = fib (s) не пересекает точек с ненулевыми SG, кроме x = 0. Рассмотрим сначала точку
х = fib (s ? 1).
В этой точке
у = fib (s) ? fib (s ? 1) = fib (s ? 2).
При p = fib (s ? 1)
q = целая_часть ((fib (s ? 1) ? 1)/2).
Нужно показать, что для каждого s
целая_часть ((fib (s ? 1) ? 1)/2) < fib (s ? 2),
или, что равносильно,
fib (s ? 1) < 2 * fib (s ? 2) + 1.
Но
fib (s ? 1) = fib (s ? 2) + fib (s ? 3)
и
fib (s ? 3) < fib (s ? 2).
Следовательно, рассматриваемая диагональ не пересекает точек с нулевым SG в fib (s ? 1). Она не может пересекать их и между s ? 1 и s, поскольку эта часть воспроизводит то, что происходит в интервале от 1 до fib (s ? 2), а диагональ, выходящая из fib (s ? 2), не пересекает точек с нулевым SG до оси q.
Вы без труда завершите это доказательство.
- 3. Игры без стратегии
- Восстановление "безнадежных" баз данных. InterBase Surgeon
- Выбор стратегии ценообразования
- Система безопасности InterBase
- Общие рекомендации по безопасности
- Надежность и безопасность
- Улучшенная стратегия вычисления предиката IN и условий, объединенных по OR
- Безопасная работа с внешними таблицами
- Конфигурация безопасности для базы данных
- Интегрированная безопасность (NT Integrated Security)
- Безопасность временных таблиц
- Безопасность внешних таблиц. Параметр EXTERNAL FILE DIRECTORY




