Книга: Программирование игр и головоломок

Сноски из книги

Я здесь совершаю плагиат по отношению к поговорке жителей плоскогорья Высоких Вивар, которая звучит так: кто сам пилит свои дрова, согревается дважды.

Строго говоря, эти рассуждения применимы к любой программе, написанной на любом языке, если только эта программа не использует никакой внешней информации в качестве исходных данных. В качестве такой внешней информации удобнее всего использовать что-нибудь связанное с временем: число изменений напряжения в сети с момента последнего включения вашего компьютера или число секунд с момента его покупки, если ваш компьютер снабжен внутренними энергозависимыми часами (на литиевой батарейке), и т. п. Обычно, на каком бы языке вы ни работали, у вас есть возможность прочесть показания внутренних часов компьютера (посмотрите в документации, как работать с таймером). — Примеч. ред.

См. предыдущую сноску. — Примеч. ред.

«Пришлите побольше денег.»

«Помогите молодому человеку.»

«Нужно, лекция, ученик.»

S — первая буква слова «somme» (фр. сумма), P — слова «produit» (фр. произведение). — Примеч. ред.

Да и от языка, который вы используете. — Примеч. ред.

Повторим эти рассуждения чуть более подробно. Пусть

a₁ = 2, a_i+1 = a_i? ? 1 mod n,

b₁ = 2, b_i+1 = b_i? mod s

— последовательности, соответствующие числам n и s соответственно. Тогда легко доказать по индукции, что b_i = a_i mod s. Одним из периодов последовательности {а_i} является n. Значит, n является периодом и для последовательности {b_i}. Известно, что любой период последовательности кратен ее минимальному периоду, Так как p, по определению, является минимальным периодом последовательности b_i, то n делится на p. — Примеч. ред.

Этот язык описан на стр.7–8 выше. Здесь лишь кратко напоминаются формы записи условных операторов и операторов цикла. — Примеч. ред.

В оригинале «master-mind». — Примеч. ред.

Так начинаются правила проведения автогонок. — Примеч. ред.

Напомним, что книга написана в начале 80-х годов. — Примеч. ред.

Таким образом, подсчитывается общая сумма карт, взятых партнерами, а не отдельные суммы для каждого партнера. — Примеч. ред.

Имеется в виду постановка Блезом Паскалем (1623–1662) вопроса о вере в существование бога как задачи о выборе стратегии в азартной игре («Мысли», отрывок 233): «Взвесим выигрыш и проигрыш, ставя на то, что бог есть. Возьмем два случая: если выиграете, вы выиграете все; если проиграете, то не потеряете ничего. Поэтому, не колеблясь, ставьте на то, что он есть» (Антология мировой философии в четырех томах, Том 2, М., «Мысль», 1970, С. 306). — Примеч. пер.

«Ослиным мостом», дальше которого учащегося сдвинуть трудно, считалась в XII–XIII вв. в Парижском университете либо теорема о равенстве углов при основании равнобедренного треугольника, либо геометрическое доказательство теоремы Пифагора. — Примеч. пер.

Вот другая и, на мой взгляд, более правильная формулировка этой задачи: циклически сдвинуть элементы n-вектора на m позиций влево. — Примеч. ред.

Нужно было бы сказать «не убывает», но получилось бы совершенно не в стиле этой книги. — Примеч. ред.

Важно и то, что никаких других позиций, кроме 0, из 1 получить нельзя. — Примеч. ред.

Читатель может вернуться к определению чисел Спрага-Грюнди и убедиться, что эти числа определяются на множестве игровых позиций раз и навсегда, исходя из правил игры, и, разумеется, не могут меняться в процессе разыгрывания конкретной партии. Что же является позицией в этой средневековой игре? — Позицией является состав выложенных на стол карт, а также их значения: сколько карт на столе имеет значение 1, сколько карт имеет значение 2, и т. д. Сумма, набранная игроками в данный момент, равна 84 минус сумма значений карт на столе. Что же имеет в виду автор книги, когда он пишет SG(50)? Почему он приписывает число Спрага-Грюнди не позиции, а сумме карт этой позиции? Дело в том, что для всех позиций с набранной суммой 50 число Спрага-Грюнди одинаково и равно 0. Это и позволяет написать равенство SG(50) = 0. А что могло бы значить SG(49)? Если бы все позиции с суммой 49 имели одинаковое число SG, мы бы обозначили его SG(49). Но, увы! Разные позиции с суммой 49 имеют разные числа Спрага-Грюнди. Так что автор книги дальше рассуждает о несуществующих вещах. Я из этих рассуждений ничего полезного извлечь не смог (кроме подозрения, что у автора нет работающей программы, играющей в 24 карты). — Примеч. ред.

Можно доказать, что в играх, подобных игре Нима и обычным шахматам, — в играх с полной информацией — выигрывающая стратегия всегда существует. Это — относительно простая теорема. Другое дело, что эта выигрывающая стратегия может быть не очень простой (Ним) или вообще еще не открытой (шахматы). — Примеч. ред.

В частном случае, когда в каждой кучке игра идет по правилам игры Нима, число Спрага-Грюнди каждой кучки равно просто числу спичек. — Примеч. ред.

Эти рассуждения безусловно справедливы, если в моем распоряжении остался один-единственный ход — тогда этим ходом я хочу «попасть в десятку», т. е. угадать искомую комбинацию. Если же ход не последний, то моя цель — получить как можно больше информации об искомой комбинации. Может случиться, что для этого выгоднее взять комбинацию вне множества, описанного автором. — Примеч. ред.

Маленькая головоломка для знающих французский (или хотя бы имеющих словарь): откуда это обозначение? — Примеч. ред.

При чтении этого абзаца вспоминается шутка Маяковского. После одного из своих выступлений он получил из зала записку: «Мы с товарищем слушали ваши стихи и ничего не поняли». Маяковский ответил: «Нужно иметь умных товарищей». — Примеч. ред.

Если разрешить перемещать каждый элемент вектора не один раз, а два, то можно найти изящное и простое решение, в котором и речи нет ни о каких общих делителях. Представим себе элементы вектора расположенными по окружности на равных расстояниях друг от друга. Нам нужно повернуть эти векторы на угол. Используйте тот факт, что всякий поворот окружности можно получить, выполнив подряд две осевые симметрии. — Примеч. ред.

См. головоломку 29. — Примеч. пер.

В математике для решения этой задачи есть полезная формула Ньютона-Лейбница:

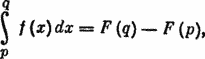
где F —функция, определяемая условием F(x) = f(x), x ? [p, q]. Впрочем, все эти интегралы нам не понадобятся, так как у этой формулы есть гораздо более простой аналог для сумм: a_i + a_i+1 + … + a_j = b_j ? b_i?1, где последовательность {b} определяется условием, что b_k ? b_k?1 = а_k для любого k от 1 до n. Последовательность {b} легко построить: b₀ = 0, b_k+1 = b_k + a_k+1. Для последовательности {b} задача ставится так: найти такие i < j, что разность b_j ? b_i максимальна. С этой задачей уже легче справиться. — Примеч. ред.

Вот пара условий, которая не обладает этим свойством: t: x ? 0; u: sin(1/x) > 0. — Примеч. ред.

Прочтя весь этот ужас, я решил провести решение, основанное на методике из курса программирования механико-математического факультета МГУ.

Каждой последовательности чисел {a₁, а₂, …, a_i} (i ? 1) сопоставим число lmax, равное максимальной длине равнинного участка этой последовательности. Очевидно, что lmax ({a₁}) = 1. Пусть мы знаем lmax ({a₁, а₂, …, a_i}). Как вычислить величину lmax ({a₁, …, a_i, a_i+1})? Добавление элемента a_i+1 к последовательности {a₁, а₂, …, a_i} не затрагивает равнинных участков этой последовательности, кроме, быть может, последнего. Если a_i+1 = a_i, то длина этого последнего участка — назовем ее llast ({a₁, …, a_i}) — увеличивается на единицу. Если величина llast ({a₁, …, a_i, a_i+1}) окажется при этом больше величины lmax ({a₁, а₂, …, a_i}), то это значит, что последний равнинный участок в последовательности {a₁, а₂, …, a_i, a_i+1} по крайней мере на 1 длиннее всех предыдущих, и, значит, lmax ({a₁, а₂, …, a_i, a_i+1}) = llast ({a₁, а₂, …, a_i, a_i+1}).

Введем четыре величины:

i — число рассмотренных членов последовательности,

lmax — максимальная длина равнинного участка для рассмотренных элементов,

llast — длина последнего равнинного участка для рассмотренных элементов,

xlast — последний рассмотренный элемент последовательности (он равен а[i]).

Теперь приведем без пояснений программу, которая вычисляет lmax ({a₁, …, an}) по индукции.

i := 1; lmax := 1; llast := 1; xlast := a[1]
нц пока i < n
x := a[i + 1]
  если x = xlast то llast := llast + 1
  иначе llast := 1 кесли
  если llast > lmax то lmax := llast кесли
  xlast := x
i := i + 1
кц
вывод lmax

Подробнее об этой индуктивной методике можно прочитать в книге: А. Г. Кушниренко, Г. В. Лебедев. Программирование для математиков. — М.: Наука, 1988. — Примеч. ред.

Оглавление книги