Книга: Программирование игр и головоломок

2. Игры с числами

2. Игры с числами

Головоломка 3.

Остановитесь, когда вы получите 5 в качестве цифры единиц с нулем «в уме».

Головоломка 4.

Представленный здесь алгоритм эквивалентен алгоритму, который можно найти в старых книгах по арифметике, и который действует на целые числа, разбитые на куски но 2 цифры в каждом куске. Вы можете либо разыскать доказательство в этих книгах, либо посмотреть в моей книге «Основы программирования», как можно доказать, что программа, реализующая этот алгоритм, действительно вычисляет квадратный корень. Но это рассуждение слишком сложно, чтобы воспроизводить его здесь.

Лично я работаю по основанию 10. Я представляю числа цепочками цифр. Присоединить 1 справа легко: это просто конкатенация. Сдвинуть вправо легко: используется индекс, сообщающий, начиная с какой позиции нужно урезать. Именно этот индекс и изменяется. Складывать с 2 легко, так как может быть не более одного переноса. Единственная тонкая операция — вычитание, Не проводите сравнения перед вычитанием: оно стоит так же дорого, как и само вычитание. Сделайте копию той части, которая должна была бы быть изменена при вычитании, и если вы обнаружите, что вы не можете осуществить вычитание, — возьмите сохраненное значение.

Головоломка 5.

Задайте три индекса и три значения: i₂, i₃, i₅, x₂, x₃, x₅. Число i₂ есть индекс элемента последовательности, который, будучи умноженным на 2, дает подходящего кандидата на роль ближайшего значения (иначе говоря, удвоение числа с индексом i₂ ? 1 дает число, которое содержится в уже сформированной части последовательности, но удвоение числа с индексом i₂ дает число, которое в сформированной части не содержится). Число x₂ получается удвоением числа с индексом i₂. Вы определяете аналогично i₃ и x₃ заменяя «удвоение» на «утроение» (произведение на 3 числа с индексом i₃ ? 1 содержатся в построенной части последовательности, а число x₃ — утроенное число с индексом i₃ — в ней не содержится). Наконец, вы делаете то же самое для i₅ и x₅. Ближайшее число в последовательности есть наименьшее из чисел x₂, x₃, x₅. Назовем его х. Если x = x₂, то i₂ увеличивается на 1 и x₂ пересчитывается. То же самое для i₃ и i₅.

Головоломка 7.

Возьмем n = 3n' + 2. Тогда (2n ? 1)/3 = 2n' + 1.

По общему правилу, непосредственно следующий за нечетным числом 2n' + 1 элемент равен (3(2n' + 1) + 1)/2 = 3n' + 2.

Если n дает n' при переходе (p, q), q > 1, т. е. если n имеет вид n = (2p(2^qn' + 1)/3^p) ? 1, то

n'' = (n ? 1)/2 = (2^p?1(2^qn' + 1)/З^p) ? 1.

Как и следовало ожидать, это имеет в точности тот смысл, что если деление на З^p можно выполнить нацело, то в связи с этим возникает соотношение между (p, q) и n'.

Если n" увеличить на 1, а затем умножить на 3^p?1/2^p?1, то получится (2^qn' + 1)/3.

Тогда нужно уменьшить результат на 1: получим (2^qn' ? 2)/3. Но это число делится на 2, так что с помощью перехода (p ? 1, 1) число n" дает

(2^q?1n' ? 1)/3.

По общим правилам получаем

3 ((2^q?1n' ? 1)/3) + 1 = 2^q?1n',

а затем n', что и доказывает наше утверждение.

Если вы примените это правило перехода к 4k + 1, то нужно добавить 1, что дает 4k + 2, делящееся на 2, но не на 4. Делим на 2 и умножаем на 3, что дает 6k + 3. Уменьшаем на 1 и затем делим на 2, и получается Зk + 1.

Если k нечетно, то это — элемент, следующий за k; так что за числом вида 4k + 1 с k нечетным следуют те же величины, что и за k.

Если k четно, то 4k + 1 дает 3k + 1.

Если существует цикл с единственным переходом p, q, т. е.

n = (2^p(2^qn + 1)/3p) ? 1,

то это возможно только в случае, когда существует такая пара p, q, что число

(З^p ? 2^p)/(2^p+q ? З^p)

— целое. Мы показали, что такой пары (p, q) нет.

Головоломка 10.

9*АВСДЕ + АВСДЕ = 10*АВСДЕ, что можно записать как АВСДЕ0. Отсюда получаем зашифрованное сложение:

FGHIJ + ABCDE = ABCDE0

Это показывает, что A = 1. Далее, J + E не может быть нулем, следовательно, J + Е = 10 и для I есть кое-что «в уме». Сумма F + A дает AB с A = 1, так что сумма F + 1, к которой, может быть, добавлено что-то «в уме», должна дать число, большее 9. Это может быть только в случаях 1 + 8 + 1 = 10, 9 + 1=10 или 1 + 9 + 1 = 11. Но, так как B ? A, то B = 0.

Тогда в сумме G + B рассмотрим цифру C как цифру единиц. Так как В = 0, то это означает, что для G «в уме» кое-что есть (потому что G ? С).

Отсюда получаем схему операции сложения:

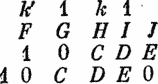
Запишем, что A + B + C + D + E + F + G + H + I + J = 45,

А = 1, B = 0.

Запишем пять операций сложения с учетом переносов в старший разряд:

J + E = 10,

1 + I + D = 10k + E,

k + H + C = 10 + D,

1 + G + В = 10k' + С,

k' + F + A = 10.

Сложим их все. Вам остается

C + D + E = 17 ? 9(k + k').

Но С + D + E не может быть меньше, чем 2 + 3 + 4 = 9, и не может быть больше, чем 6 + 7 + 9 (если F = 8 и k' = 1). Не может быть, чтобы у вас одновременно выполнялись соотношения k = k' = 1 (что давало бы отрицательную сумму С + D + E). Но не может быть и равенства k + k' = 1, так как тогда было бы С + D + E = 17 ? 9 = 8, что слишком мало. Следовательно, k = k' = 0. Составим окончательную систему

J + E = 10,

I + D + 1 = E,

H + C = 10 + D,

G + 1 = С,

F = 9.

Закончите вы с помощью программы.

Головоломка 11.

Обозначим через a_i цифры исходного числа, b_i — цифры результата, k_i — цифры «в уме»:

3a_i + k_i = b_i + 10k_i+1.

Сумма всех a_i равна 45, как и сумма всех b_i. Обозначим через K сумму всех k_i:

3*45 + K = 45 + 10*K дает К = 10.

Мы знаем, что дает «в уме» каждая цифра:

1 дает 0, 2 дает 0, 3 дает 0 или 1 в зависимости от того, что хранится «в уме» над 3.

4 дает 1, 5 дает 1, 6 дает 1, потому что не может случиться 3*6 + 2, что давало бы «в уме» 2, но цифру единиц 0;

7, 8 и 9 дают 2.

Для того, чтобы сумма величин «в уме» была равна 10, нужно, чтобы 3 давало 1 «в уме». Так как 3*3 + 1 (с цифрой единиц, равной 0) случиться не может, то нужно, чтобы «в уме» над 3 было 2. Следовательно, 3 стоит слева от 7, 8 или 9. В частности, 3 не может стоять на правом конце.

Остальное просто, если вы будете следовать методу, указанному в разделе «Условия». Вот таблица:

Потребуем, чтобы 9 было справа; следовательно, вычеркнем 9 из этой таблицы, оставив его только в столбце, соответствующей тому, что «в уме» 0. Цифра 3 требует 2 «в уме», чтобы дать 1. Вычеркнем остальные 3 в таблице. Цифра 9 не может быть получена иначе как с помощью 6 и 1 «в уме». Другие 6 вычеркиваем. Цифра 8 получается из 2 при 2 «в уме». Нужно взять 3 числа в первом столбце, так что нужно еще одно не равное ни 2, ни 3. Их нужно 4 в среднем столбце, так что нужно еще 3 числа, ре равных 6, которые нужно взять среди цифр 7, 4, 1, 8, 5. Два последних числа должны быть взяты из столбца с нулем «в уме». Когда эти числа среди всех возможных будут выбраны, останется расположить их в соответствии с тем, что должно быть для них «в уме». Эту программу сделать легко.

Головоломка 12.

Если число a₁a₂…ap (представленное как последовательность цифр) кратно 3, то и a₁ + а₂ + … + ap кратно 3. Сумма кубов цифр равна

a₁³ + а₂³ + … + ap³.

Нужно показать, что это число также кратно 3. Действуйте по индукции по числу слагаемых. Предположим, что для p = n ? 1 членов

a₁³ + а₂³ + … + ap³ = (a₁ + … + ap)³ по модулю 3; тогда равенство

(a₁ + … + ap + an)³ = (a₁ + … + ap)³ + an³ + 3 (…)

доказывает наше утверждение для n слагаемых.

Возьмите число с k цифрами. Сумма кубов его цифр ограничена величиной k*9³. Но исходное число не может быть меньше, чем 10^k?1. Следовательно, достаточно, чтобы 10^k?1 было больше, чем k*729, что очевидным образом выполняется при k = 5. Но эта оценка слишком пессимистична.

Головоломка 14.

Число, полученное при обращении порядка цифр, равно

1000d + 100c + 10b + a,

и разность этих двух чисел равна

999 (a ? d) + 90 (b ? c).

Числа a, b, c, d были расположены в невозрастающем порядке, и они не все равны между собой, так что a строго больше d и a ? d не равно нулю. Все остальное просто.

Головоломка 16.

Единственное, что до сих пор еще не сказано — это способ определять, становится» ли последовательность периодической. Метод Полларда был основан на первой стратегии. Мы выясняем, существует ли a_i с a_2i = a_i. Но вычисление f(x) = x² ? 1 по модулю n — дорогое вычисление. Брепт улучшил этот метод, предложив использовать вторую стратегию.

Головоломка 17.

Эта программа основана на следующих результатах:

если b нечетно, n четно, то n делится на b тогда и только тогда, когда n/2 делится на b;

нечетное n делится на b тогда и только тогда, когда n ? b делится на b. Но n ? b четно.

Для n = 2⁷⁷ ? 3 и b = 7 вы получаете:

Число n нечетно. Рассматриваем n ? b = 2⁷⁷ ? 10. Оно делится на 2: получаем 2⁷⁶ ? 5.

Это число нечетно: (2⁷⁶ ? 5) ? 7 = 2⁷⁶ ? 12.

Делим на 4: 2⁷⁴ — 3.

Получаем ту же самую задачу, в которой показатель уменьшен на 3. Так как 77 = 3*25 + 2, то мы таким образом доходим до 2² — 3 = 1, которое не делится на 3. Вряд ли вас слишком утомит доказательство того, что 2ⁿ ? 3 никогда не делится на 7…

Головоломка 18.

Я не в состоянии рассказать вам, как я получил эту программу, это — очень долгая история, связанная с разложением целых чисел на множители. Может быть, когда-нибудь я ее и опубликую. Следовательно, будем разбираться в том, что нам дано — в тексте программы.

Начнем с нечетного n. В соответствии с инициализацией программы n = 4p ? 1, где p четно. В противном случае уже последует ответ «НЕТ». Следовательно, рассмотрите нечетное n, являющееся полным квадратом и, следовательно, квадратом нечетного числа 2k + 1;

(2k + 1)² = 4k² + 4k + 1 = 4k (k + 1) + 1.

Так как k (k + 1) — произведение двух последовательных целых чисел, и из двух последовательных целых чисел всегда есть хотя бы одно четное число, получаем простой, но интересный результат: любой квадрат нечетного числа сравним с 1 по модулю 8. Таким-образом, при n отличном от 1 по модулю 8 инициализирующая часть программы выводит, что n не является точным квадратом.

Посмотрим теперь, что происходит внутри цикла. Делим p на 2, и если результат четен, мы удовлетворяемся тем, что умножаем a на 2. При этом действии произведение a*p остается постоянным. Поэтому кажется вероятным, что в цикле существует инвариантная величина, запись которой содержит a*p в предположении, что p четно.

Если после деления p на 2 результат оказывается нечетным, то мы вычитаем из этого результата a/2 + b. Обозначим новые значения a, b, p через а', b', p' соответственно:

а' = 2*а, p' = p/2 ? а/2 ? b, b' = a + b.

Для этих значений получаем:

a'*p' = a*p ? a² ? 2a*b = а*р ? (а + b)² + b² = а*р ? b'² + b².

Это, наконец, дает

а'*p' + b'² = а*р + b².

Инвариантной величиной цикла оказывается, таким образом, сумма ар + b², причем p остается четным. Это обеспечивается тем, что в случаях, когда p/2 нечетно, мы вычитаем нечетные b из нечетного p/2. Что касается b, то он нечетен потому, что он начинается со значения 1 и к нему прибавляются только четные значения а.

В начале а = 4, p (целая часть дроби (n ? 1)/4) четно, b = 1, так что ар + b² = n.

Наконец, a, начиная с 4, умножается на 2 при каждом прохождении цикла; b начинается с 1, которое меньше соответствующего начального а = 4.

Тогда при переходе от a, b, p к a', b', p' либо

b' = b, а' = 2*а, так что если b < а, то и b' < а';

либо

b' = а + b, а' = 2*а, что также сохраняет справедливость отношения а' < b'.

Следовательно, вот ситуация, которую цикл оставляет инвариантной:

n = а*p + b²;

а — степень двойки,

p четно,

b нечетно, b < а.

Кроме того, мы знаем, что при выходе из цикла p < а.

Если p равно нулю, то n = b². Тогда мы видим, что n — квадрат числа b, которое выводится, и все закончено.

Но n может оказаться полным квадратом и тогда, когда p не нуль. Попробуем рассмотреть все возможные случаи. Положим n = r² (r нечетно). Соотношение

r² = ар + b дает

r² ? b² = ар.

Положим r + b = 2u, r ? b = 2v (r и b нечетны). Отсюда получаем 4uv = ар.

Поскольку r = u + v, где r нечетно, получаем, что u и v не могут быть числами одинаковой четности, так что одно из них четно, а другое нечетно. Так как а является степенью двойки, то нечетный сомножитель относится к p. Выявим его, полагая р = s2^t, где s нечетно, a t ? 1 (p четно).

Напомним, что а = 2^k. В этих обозначениях 4uv = ар = s2^k+t, uv = s2^k+t?2.

Возможные решения для пары u, v имеют вид пар

s'2^k+t-2, s''

где s's" = s.

Покажем сначала, что s" — меньший из этих двух элементов пары. Вследствие t ? 1 имеем k ? t ? k + t ? 2.

Вследствие p < а последовательно выводим

s2^t < 2^k,

s's"2^t < 2^k.

s's" < 2^k-t ? 2^k+t-2 ? s'²2^k+t-2

(потому что s' нечетен и не меньше 1).

Следовательно, нужно взять u = s'2^k+t-2, v = s".

Покажем теперь, что нужно обязательно взять s' =1, s" = s. По выбору u и v

b = 2^k+t?2s' ? s" < а = 2^k.

Отсюда получаем:

s" > 2^k+t?2s' ? 2^k,

и, так как t ? 1:

s" > 2^k?1s' ? 2^k,

s = s's" > 2^k?1s'² ? 2^ks = 2^k?1s' (s' ? 2).

Вследствие р = s2^t < а = 2^k выводим s < 2^k?t ? 2^k?1.

Объединим два полученных неравенства:

2^k?1s' (s' ? 2) < x < 2^k?1, поэтому s' (s' ? 2) < 1.

Единственное нечетное число s', удовлетворяющее этому соотношению, это s' = 1. Следовательно, у нас остается единственная возможность:

u = 2^k+t-2, v = s,

b = u ? v = 2^k+t-2 ? s < а = 2^k,

s > 2^k+t-2 ? 2^k.

Так как s < 2^k?t, то t должно быть таким, чтобы

2^k?t > 2^k+t-2 ? 2^k.

Поскольку t должно быть строго положительно, то его единственными возможными значениями являются t = 1 и t = 2.

При t = 1 имеем

p = 2s, b = 2^k?t ? s = a/2 ? p/2.

Следовательно, если 2b = а ? p, то n — квадрат числа (а + p)/2 = а ? b.

При t = 2 имеем

p = 4s, b = 2^k ? s = a ? p/4.

Следовательно, если p = 4(a ? b), то n — квадрат числа a + p/4 = 2а ? b.

Этим исчерпываются случаи, когда n может быть полным квадратом.

Можно спросить себя, могут ли эти различные случаи действительно осуществляться. Заметим, что при вступлении в цикл у нас b = 1, a = 4. После этого b может быть изменено добавлением а, т. е. кратным числа 4. Следовательно, b остается сравнимым с 1 по модулю 4. В трех возможных случаях:

p = 0, r = b,

p = а ? 2b, r = a ? b,

p = 4 (a ? b), r = 2a ? b,

первый случай — единственный, в котором квадратный корень из n сравним с 1 по модулю 4; два других дают квадратный корень, сравнимый с 3 по модулю 4. При выходе из цикла равенство

b = ар + b²

с учетом соотношений p < a, b < a дает n < 2a² и, следовательно, при выходе из цикла a² > n/2. Равенство

ар = n ? b²

дает p = (n ? b²)/a < n/а.

Если окажется, что n/а < a, то непременно p < а и цикл закончен. Чтобы цикл остановился, необходимо, чтобы a² > n/2, и цикл заведомо останавливается, если a³ > n.

Следовательно, все зависит от положения n по отношению к степеням двойки. Существует такое целое n, что

4^q < n < 4^q+1.

Возможны два случая. Во-первых, может выполняться неравенство

4^q = 2^2q < n < 2^2q+1,

и тогда для k = q число a² = 2^2q > n/2 может быть значением остановки, но в этом нет уверенности. С другой стороны, если

2^2q+1 < n < 2^2q+2,

то единственное значение a, удовлетворяющее условию a² > n/2, есть a = 2^q+1, и для этого значения имеем a² > n, что гарантирует остановку. Поскольку r = a ? b, то а = r + b > r и, следовательно, a² > n.

Во втором случае

r = 2a ? b и b < а, откуда а < 2a ? b = r.

Таким образом, все три распознаваемые программой случая являются единственными возможными исходами программы, и каждый из них может произойти.

Таким образом, перед нами — очень забавный алгоритм, который дает значение квадратного корня, и который определяет случай, когда n не является корнем, но в этом случае не дает никакой дополнительной информации.

Программа заведомо останавливается при а = 2^q+1, так что число шагов цикла не больше q ? 1 (начиная с 4), причем q — логарифм квадратного корня из n по основанию 2. Таким образом, получилась программа порядка In n, что дает ту же сложность, что и обычный алгоритм, действующий кусками по две цифры. Но для этого последнего алгоритма нужен еще первый цикл, чтобы найти порядок величины n.

Головоломка 19.

Соотношение f(a, b) = f(b, a) следует из самой инициализации p и q:

p := max (a, b); q := min (a, b).

Эти две функции симметричны по a и b, и поэтому точно так же симметрична f. При анализе программы мы ограничены действиями, происходящими внутри цикла. Величины r и s являются вспомогательными переменными, которые не оставляют никакой проблемы. Трудность вызывают преобразования, проделываемые над p и q. Чтобы ясно увидеть эту трудность, осуществим введение новых переменных без разрушения старых. Перепишем наш цикл:

ПОКА q ? eps ВЫПОЛНЯТЬ

r := (q/p)²; s := r/(r + 4)

p' := (2 * s + 1) * p; q' := s * q

p := p'; q := q'

ВЕРНУТЬСЯ

Рассмотрим действия этой программы, производимые над данными a, b с одной стороны и над ac, bc с другой.

Когда мы входим в цикл, то и p, и q умножаются на с при переходе от первого вычисления ко второму.

Это не меняет величины r и, следовательно, не меняет величины s. Таким образом, p и q в этих вычислениях умножаются на одни и те же сомножители, так что значения p', q' во втором вычислении получаются из значений p, q в первом вычислении умножением их обоих на c. Следовательно, мы еще раз входим в цикл при том же соотношении между входными данными; следовательно, это соотношение будет иметь место при каждом входе в цикл, и, следовательно, также и на выходе из цикла. Отсюда получаем, что f(ac, bc) = cf(a, b).

Выполнение программы для вычисления g(x) = f(x, 1) с x = 1 и eps = 10^-5 дает мне результат, равный 1.4142.

Дальше считать бесполезно, это ?2.

Я немедленно изменяю программу, чтобы она выполняла вывод не только величины g, но также и g². Я получаю:

x g²(x)

1 2

2 5

3 10

4 17

Нет возможности сомневаться: g(х) = ?х² + 1.

Перенося эту формулу в соотношение между f и g, мы видим, проделав все вычисления, что

f (a, b) = ?a² + b².

«Осталось только» доказать это. Мы не можем доверять заверениям программистов, утверждающих, что их программа делает то-то и то-то. При входе в цикл p и q имеют значения а и b в каком-то порядке, поэтому

p² + q^{2 =} a² + b².

Что происходит с величиной p² + q² после изменений, которым p и q подвергаются в цикле? Вычислим p'² + q'²:

p'² + q'² = (2s + 1)²p² + s²q² = s² (4р² + q²) + 4sp + р².

Вычислим s:

r := q²/p², s = r/(r + 4) = q²(q² + 4p²),

откуда, наконец,

s (4р² + q²) = q².

Возвращаясь отсюда к предыдущему соотношению, получаем

p'² + q'² = sq² + 4sp² + р² = s(4р² + q²) + p² = p² + q².

Таким образом, все кончено… Это соотношение гарантирует, что p² + q² является инвариантом цикла. При каждом входе в цикл выполняется соотношение

p² + q^{2 =} a² + b².

При выходе из цикла

p² + q^{2 =} a² + b², причем q < ерs.

Отсюда следует, что

p² = (a² + b²) * (1 ? q²/(a² + b²)).

Cpaey получаем, что

p = ?a² + b²

с относительной ошибкой eps²/(2 * (a² + b²)).

Чтобы получить точность до 10^-5, совершенно ненужно брать eps = 10^-5; более чем достаточно eps = 0.004. Эта программа сходится очень быстро.

Оглавление книги