Книга: Программирование игр и головоломок

4. Игры со стратегией

4. Игры со стратегией

Игра 16. Числа Спрага-Грюнди

В большинстве нижеследующих игр два игрока делают ходы по очереди, и выигрывает тот, кто достигает некоторой намеченной в начале игры позиции. В той игре, которую мы обсуждаем сейчас, позиция может быть полностью охарактеризована числом оставшихся спичек, и выигрывающая позиция соответствует числу спичек, равному нулю. Спраг и Грюнди предложили (соответственно в 1936 и 1939 годах) связывать с каждой игровой позицией неотрицательное целое число следующим образом:

— выигрывающей позиции вы сопоставляете 0;

— данной игровой позиции вы сопоставляете наименьшее неотрицательное целое, отличающееся от чисел, связанных с позициями, которые могут быть достигнуты, исходя из данной.

Образуем числа Спрага-Грюнди для этой игры.

Позиции 0 сопоставляется число 0, SG (0) = 0.

Исходя из 1, можно получить 0 (поскольку мы имеем право удалить одну спичку[19]. Следовательно, SG(1) — наименьшее неотрицательное целое, отличное от 0, или SG(1) = 1. Исходя из 2, можно получить 1 и 0. Следовательно, SG(2) — наименьшее неотрицательное целое, отличное от 0 и 1, поэтому SG(2) = 2.

Так как можно удалять спички вплоть до 6, то точно так же имеем

SG(3) = 3, SG(4) = 4, SG(5) = 5, SG(6) = 6.

Предположим теперь, что имеется 7 спичек. Можно удалить от 1 до 6. Поэтому в результате можно получить от 6 до 1 спичек, но не 0. Число SG(7) — наименьшее неотрицательное целое, отличное от 1, 2, 3, 4, 5, 6, Следовательно, это 0.

SG(7) = 0,

А теперь из 8 можно получить от 2 до 7, поэтому SG(8) — это не 2, не 3, …, не 6 и не 0, поэтому оно равно 1.

SG(8) = 1.

Теперь вы можете установить общий закон:

SG(p) = остаток от деления p на 7.

Как же выигрывать?

Если вы после своего хода можете оставить кучу, для которой число Спрага-Грюнди равно 0, то ваш противник не сможет достичь ситуации с числом нуль, поскольку по определению число, которое он оставит, отлично от исходного числа. Поскольку он не сможет достичь ситуации p с SG (p) = 0, то он и не может выиграть. Ему придется оставить вам ситуацию с SG(p) ? 0, исходя из которой, вы всегда сможете получить ситуацию с числом Спрага-Грюнди, равным нулю. Следовательно, вам нужно оставлять вашему противнику число спичек с числом SG, равным нулю, иначе говоря, число спичек, кратное 7.

Одно из двух: либо ваш противник не знает этого правила и играет «по нюху»; при первой возможности вы оставляете ему кратное 7 и из ежовых рукавиц не выпускаете; либо он знает правило и ходит первым: он достигает кратного 7. Вы не сможете выиграть, если он не рассеян или не сделает ошибки в счете. Но компьютер не рассеян и не делает ошибок в счете (если ваша программа верна)…

Игра 17.

Выигрывающее положение — 31 декабря. Возьмите листок бумаги в клетку. Расположите по абсциссе месяцы, а по ординате дни. Так как 31 декабря выигрывает, то вы обозначаете эту точку числом Спрага-Грюнди 0. Из каждого дня декабря можно получить 31, но также и любой другой последующий день. Поэтому вы приписываете значение 1 дате 30 декабря, значение 2 дате 29 декабря, и т, д. То же для любого 31 числа; из него можно получить 31 число всех последующих месяцев. Поэтому 31 октября получает 1, 31 августа 2 и т. д.

После этого вы можете закончить значение таблицы и приписать число Спрага-Грюнди всем дням года. Вы увидите также появление дней со значением 0, которые являются выигрывающими днями. Напоминаю вам правило: каждому игровому положению приписывается наименьшее неотрицательное целое значение, отличное от значений тех положений, которые можно получить, исходя из данного, т. е. в настоящем случае — от значений тех положений, которые расположены правее, и тех, которые расположены ниже.

Закон заполнения таблицы достаточно сложен; и я не пытаюсь вам его сформулировать. Как только октябрь заполнен, появляется простая закономерность, которая дает соотношение между номером дня и номером месяца для выигрывающих положений.

Даже если вы мало знаете современную математику, вы слышали разговоры об отношении эквивалентности. Все выигрывающие положения эквивалентны. Игровое положение задается парой д, м, где д — номер дня, а м — номер месяца. Следовательно, вы должны найти такое отношение эквивалентности для пар натуральных чисел, чтобы

д, м' было не эквивалентно д, м при м ? м', и

д', м было не эквивалентно д, м при д ? д'.

Наконец, для выигрывающей позиции д, м должно быть эквивалентно 31, 12. Что-то похожее на это можно видеть в программах лицеев…

Я прекрасно понимаю, что календарь осложняет все, поскольку длина месяца не постоянна и зависит от м, причем к тому же с непростым законом изменения. Но, к счастью, оказывается, что это никак не сказывается на этом замечательном отношении эквивалентности.

После всего сказанного вы должны выпутаться из этой задачи…

Игра 18.

Эта игра — производная от средневековой игры. Сначала попытайтесь достичь 50 с точностью до кратного 7. Но как только все четыре карты, имеющие одинаковое значение, оказываются использованными, так ситуация сразу меняется. Вот пример начала партии,

Я беру туза, компьютер тоже. Сумма 2.

Чтобы получить 8, я беру 6. Компьютер берет туза. Сумма 9.

Чтобы получить 15, я снова беру 6.

Компьютер берет последнего туза. Сумма 16,

Теперь остаются следующие карты:

2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5 6 6

Так как тузов больше нет, то числа Спрага-Грюнди изменились[20]. Теперь из 49 больше нельзя получить 50.

SG(50) = 0, SG(49) = 0.

Из (48) можно получить 50. Поэтому SG(48) = 1.

Из 47 можно получить 49 и 50, но не 48. Поэтому SG(47) = 1.

Теперь положения, имеющие нулевое SG, — это

42 41 34 33 26 25 18 17

Поэтому я могу взять 2, чтобы достичь 18.

Стратегия усложняется, поскольку числа Спрага-Грюнди полностью меняются при удалении каждой карты. Но это как раз и благоприятствует компьютеру. Если он не может достичь выигрывающего положения, он берет карту, оставшуюся в наименьшем количестве экземпляров. Каждый раз, когда тот или иной тип карт исчерпывается, компьютер пересчитывает заново числа Спрага-Грюнди.

Мне придется переписать мою программу в соответствии с этой стратегией.

Игра 19. Ним-сумма.

Для меня эта игра — своего рода педагогический вызов. Я чрезвычайно раздражен тем, что все, кто излагает эту игру, ведут себя одинаково: известно, что выигрывающей стратегией является следующая… Почему она выигрывает? Откуда она вообще взялась эта стратегия?

Выписать числа Спрага-Грюнди очень трудно.

Попытаемся найти несколько выигрывающих положений.

Если к моменту своего хода я обнаруживаю только одну спичку, то я выигрываю.

Если я обнаруживаю единственную кучку, то я тоже выигрываю.

Если, кроме одной кучки, ничего больше нет, то можно положить SG(0) = 0 (я выигрываю, я взял последнюю спичку), вследствие чего SG(n) = n.

Предположим теперь, что у нас две кучки. Если я оставляю две кучки, в каждой из которых по одной спичке, то я обязательно выигрываю: мой противник должен взять столько спичек, сколько он хочет, но — только из одной кучки. У него нет выбора, он может только взять одну из спичек, после чего я возьму последнюю спичку и выиграю.

Если я оставляю две одинаковые кучки по n спичек в каждой, то у моего противника две возможности:

— взять целиком одну из кучек, я возьму другую и выиграю;

— взять часть одной из кучек и оставить в ней n' спичек. Я возьму столько же из другой, оставляя ситуацию n', n'. По индукции — я на пути к победе.

В наиболее общем случае ситуация характеризуется p целыми числами (p — число кучек). При каждом ходе изменяется одно и только одно из этих неотрицательных целых чисел и оно заменяется меньшим неотрицательным целым числом, которое может быть и нулем. Если мы исходили из выигрывающей ситуации, то новая ситуация не является выигрывающей. Если ситуация не являемся выигрывающей, то всегда можно, уменьшая одно из чисел, получить выигрывающую ситуацию (по крайней мере, если выигрывающая стратегия существует[21]…).

Попытаемся охарактеризовать числа с помощью их цифрового представления. Изменить число — значит, изменить представляющие его цифры. Если использовать десятичное представление, то у нас в наличии 10 возможных цифр и их изучение затруднительно. Возьмем двоичное представление, для которого есть только две возможные цифры: 0 и 1. Уменьшение числа изменяет по крайней мере одну цифру этого числа, так что есть по крайней мере одна цифра 1, замененная на 0, или 0, замененный на 1. Этого должно хватить для того, чтобы заставить перейти от выигрывающего положения к проигрывающему положению. Число 0 встречаться не должно, поскольку пустые кучки, характеризующиеся нулевыми значениями, просто не считаются кучками. Характеризация выигрывающего положения должна быть поэтому связана с единицами различных чисел, записанных в двоичной системе.

Если есть две кучки с одинаковым числом спичек, то ситуация является выигрывающей. Следовательно, каково бы ни было число единиц в двоичном представлении каждого числа, положение является выигрывающим, если в каждом разряде наши два числа имеют либо 0, либо две цифры 1.

Первые выигрывающие комбинации с тремя кучками имеют вид

1, 2, 3, или в двоичной записи 01 10 11,

1, 4, 5, или в двоичной записи 001 100 101

Опять в каждом разряде наши три числа имеют либо 0, либо две цифры 1. Я разобрал достаточно случаев, чтобы подвести вас к результату К. Бутона (1902): положение является выигрывающим, если в каждом двоичном разряде суммарное число 1 двоичных представлений числа спичек в каждой кучке четно.

Совершенно очевидно, что нужно совершить прыжок для перехода от случая двух куч или первых примеров в случае трех куч к Наиболее общему случаю. Тут требуется выдумка или изобретение. Следует, иметь мужество признать, что некоторые люди имеют настоящий талант изобретать или открывать то, что совершенно не очевидно, и не всегда можно потом сказать: да никакой заслуги в этом нет, это было очевидно. Нет, это остается тайной, и преподавателя раздражает, если он оказывается вынужден давать результат, который нельзя легко «переоткрыть».

Назовем Ним-суммой двух целых чисел p и q число, которое вычисляется следующим образом:

p и q записываются в двоичной системе;

сложение выполняется поразрядно, по следующему правилу:

0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 0

(сложение без переноса в следующий разряд).

Рассмотрим игру, образованную объединением n независимых игр, каждая со своими собственными правилами. Игра проходит в кучке 1 но правилам R1, в кучке 2 — по правилам R2, … в кучке n — по правилам Rn. В каждой кучке мы располагаем числом Спрага-Грюнди, зависящим от числа спичек в этой кучке. Число Спрага-Грюнди есть Ним-сумма чисел Спрага-Грюнди в каждой кучке…[22] Красиво, не правда ли?

Обратимся к программированию обычной игры города Нима (одно и то же правило для всех кучек: можно брать столько спичек, сколько пожелаешь, но не меньше одной). Вам нужно вычислить Ним-сумму данной ситуации. Если она равна нулю, то у вас нет шансов: ситуацию придется изменить и она перестанет быть выигрывающей. Вы можете, например, взять одну спичку из самой большой кучи: это — способ замедлить конец, и вы всегда можете ожидать, что ваш противник допустит ошибку…

Если же эта сумма не равна нулю, то это в точности означает, что есть разряды, в которых при двоичном представлении единицы встречаются нечетное число раз. Рассмотрим крайний левый из таких разрядов. Нужно уменьшить число единиц в этом разряде. Выберите кучку, содержащую единицу в этом разряде (все равно какую: взять ли самую большую, первую или последнюю…). Нужно уменьшить эту кучку на «эту» единицу. Кроме того, в любом другом (расположенном правее) разряде, где стоит нечетное число единиц, нужно

если в данной кучке в этом разряде стоит 1, удалить ее;

если в данной кучке в этом разряде стоит 0, заменить его на 1.

Это дает вам новое число спичек в этой кучке.

Я видел в некоторых книгах программы для игры Нима, в которых после обнаружения ситуации с ненулевой Ним- суммой испытывались все возможные конфигурации, чтобы найти конфигурацию с нулевой Ним-суммой. Над кем они смеются?

В игре Нима вам нужно для каждого хода, делаемого компьютером, получить двоичное представление числа спичек в каждой кучке. Вам следует решить, будете ли вы пересчитывать его при каждом ходе или вы будете сохранять различные представления, так как имея единственное представление, вы после каждого хода должны изменять его…

Я полагаю, что вы знаете, как получать двоичное представление числа, Пусть

n = ap2^p + a_p?12^p?1 + . .. + a₂2² + a₁2 + а₀.

Если разделить n на 2, вы получаете в остатке а₀, крайнюю справа цифру двоичного представления, а частное

ap2^p?1 + a_p?12^p-2 + . .. + a₂2 + a₁,

которое также является двоичной записью целого числа, получаемой из предыдущей записи вычеркиванием ее крайней правой цифры. По индукции (или, что то же самое, рекурсивно или итеративно) вы получите все двоичные цифры числа n справа налево.

Восстановление значения числа, исходя из двоичных цифр, производится в обратном порядке, слева направо, Сначала вы вычисляете

x₀ = ap,

x₁ = 2x₀ + a_p?1 = 2ap + a_p?1,

x₂ = 2x₁ + a_p-2 = ap2² + a_p?12 + ap_-2,

и т. д. Последнее x есть искомое значение,

Игра 20.

Об этой игре я вам больше ничего не скажу. Совершенно необходимо, чтобы вы хотя бы время от времени работали, Впрочем, если я вам ничего не говорю, то дело, вероятно, в том, что я вам уже достаточно рассказал. Это — новая головоломка: выясните, почему у меня нет нужды что- либо вам еще говорить…

Игра 21.

Не протестуйте, я вам помогу… Что бы вы без меня делали? Но кстати, нужно быть честным — я был вдохновлен книгой Роуза Болла [BAL].

В начале игры у вас одна-единственная строка: Спраг-Грюнди… По прошествии некоторого времени она разбивается на много строк, и связанное с ними число Спрага-Грюнди есть Ним-сумма чисел Спрага-Грюнди для каждой строки. Следовательно, нужно вычислить числа Спрага-Грюнди для одной строки, и этого будет достаточно, Вот начало:

0 SG(0) = 0

Из 1 вы достигаете 0: SG(1) = 1.

Из 2 вы достигаете либо 1, либо 0. Поэтому SG(2) — наименьшее целое неотрицательное, отличное от 0 и 1; следовательно, SG(2) = 2.

Исходя из 3, вы можете получить либо одну строку с 2 спичками (SG = 2), либо одну строку с одной спичкой (SG = 1), либо две строки по одной спичке в каждой (удалив среднюю спичку). Но число SG(1, 1) есть Ним-сумма 1 в 1 и потому равно нулю. Следовательно, SG(3) равно трем. Таким же образом вы находите

0 1 2 3 1 4 3 2 1 4 2 6 4 1

Р К. Ги доказал, что начиная с 71, эта последовательность становится периодической с периодом 12. Я не представляю себе, для чего это может быть вам нужно — разве что, если это доставит вам удовольствие, чтобы передоказать его.

Задайте компьютеру таблицу первых чисел Спрага-Грюнди, снабдите его Ним-суммой. Остальное просто.

Игра 22.

Каждая вершина может быть связана с 5 другими, что создает 6 ? 5 = 30 связей. Но каждая из них считается дважды (связь между A и B и между B и A). Поэтому есть 15 отрезков, которые нужно провести. Если игра полностью сыграна и все пути пройдены, то у одного из игроков на чертеже должно быть 8 отрезков (у того, который начинает). Они связывают 16 вершин, и поскольку в игре участвует только 6 вершин, то имеется хотя бы одна вершина, из которой выходят три отрезка. Пусть B, C и D — достигаемые этими отрезками вершины (см. рис. 36). Либо этот игрок прошел один из путей связывающих эти вершины, и тогда он проиграл. Либо он ни одного из них не провел, и тогда их провел его противник и противник проиграл…

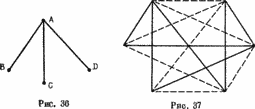
Может оказаться, что проведено 14 отрезков, не образующих треугольников (как показано на рис. 37).

В этой позиции можно быть уверенным, что кто начинал, тот и проиграет, поскольку нет возможности свести партию вничью. Число возможных комбинаций очень велико, и вы не можете ожидать, что компьютер перепробует все возможные комбинации, прежде чем принять решение. Нужно отказаться от комбинаторных соображений и играть эвристически. Первый ход, если его делает компьютер, не важен: все прямые равноценны. После этого у компьютера остается не более 14 возможных линий, и он их все исследует. Каждой из них он сопоставляет вес: О, если эта линия завершает треугольник из его линия, и он тем самым проигрывает; 1, если эта линия завершает треугольник для его противника, так как она оставляет противнику шанс проиграть; максимальный вес, если эта линия связывает еще не использованные вершины. Когда все линии испытаны таким образом, компьютер делает ход с наибольшим весом. Его стратегия оценит шкалу весов, которые вы будете выбирать.

Игра 23.

В этой игре вы не можете охарактеризовать ситуации числом спичек, оставшихся в кучке, потому что этого недостаточно; нужно еще знать, сколько спичек только что было взято, так как именно это определяет максимальное число спичек, которые вы можете взять. Поэтому нужно определить ситуацию парой

p: число спичек, оставшихся в кучке,

q: число спичек, которое только что было взято.

Положение 0 является выигрывающим, каково бы ни было число спичек, только что взятых, чтобы достичь этого состояния:

SG(0, q) = 0.

Исходя из 1, мы всегда проигрываем, поскольку обязаны взять единственную оставшуюся спичку:

SG(1, q) = 1.

Если у вас осталось две спички, то всегда можно одну взять и одну оставить, следовательно, SG(2, q) ? 1, или можно взять две и закончить игру:

SG(2, q) = 2.

Начиная с трех, выбор меняется.

Для 3, 1 ваш противник может взять 1 и оставить пару 2, 1, следовательно, SG(3, 1) ? 2, либо взять 2 и оставить пару 1, 2, так что SG(3, 1) ? 1. Но большее количество изымать нельзя. Наименьшее неотрицательное целое, отличное от 1 и 2, есть 0:

SG(3, 1) = 0.

Если вы оставляете 3, взяв больше, чем одну спичку, то противник может взять и 3, достигая 0 с SG (0, 3) = 0, и, следовательно,

SG(3, q > 1) = 3.

Все, что от вас здесь требуется — продолжить это изучение достаточно далеко, чтобы дать компьютеру список выигрывающих положений, — и тогда ваша программа будет непобедимой.

Игра 24.

Я много раз излагал нижеследующее различным программистам и каждый раз оставался в недоумении, видя, что они не считают это «очевидным».

Вы играете в «Гениального отгадчика», вы ищете неизвестную комбинацию; чтобы сделать это, вы предлагаете комбинации c₁, c₂, …, c_k. Для каждой из них вы получаете ответ о числе белых и черных шашек:

б₁, ч₁; б₂, ч₂; …; 6_k, ч_k.

Следующая предлагаемая комбинация должна быть такой, которая при сравнении с c₁ дает ч₁ черных и б₁ белых шашек; …; при сравнении с c_k она должна давать ч_k черных и б_k белых шашек. Почему? Вы ищете неизвестную комбинацию. Но эта комбинация дает при сравнении с комбинацией c_i именно ч_i черных и б_i белых шашек. Бесполезно искать решение вне множества комбинаций, обладающих этим свойством: там его не может быть[23].

Следовательно, у вас есть простая стратегия. Допустите, что вы уже каким-то образом выбрали x первых комбинаций, где x фиксировано. Компьютер располагает значениями ч_i, б_i для i от 1 до x. Вы предоставляете ему возможность перепробовать все комбинации и запоминать только те, которые дают при сравнении с уже испытанными комбинациями правильные значения черных и белых шашек.

Так как возможных комбинаций много, то нужно попытаться не перебирать их все заново при каждой следующей попытке. Вы можете, например, начать с первой позиции новой комбинации. Вы присваиваете ей первый цвет, а затем смотрите, сколько черных шашек он образует с уже испытанными комбинациями. Если он дает черную шашку с комбинацией, с которой ее не следует давать, то этот цвет нужно отбросить. Когда вы уже нашли подходящий цвет для этой позиции, переходите к следующей. Она может дать вам слишком много черных шашек, и это событие очень даже вероятно. Мало таких комбинаций, которые черных шашек не дают совсем, и больше таких, которые дают не более одной. То, что было зафиксировано для первого цвета, не может быть использовано для второго, Но заметьте, что у вас есть и другой случай для отбрасывания: если нужно получить три черных шашки при сравнении с некоторой комбинацией и если первая позиция никакого вклада не вносит, то необходимо, чтобы вторая позиция вносила свой вклад (предполагая, что есть 4 позиции). Действуя таким образом, вы достигаете в конце концов комбинации с правильным числом черных шашек. Тогда нужно проверить белые. Если они принимают нужные значения для всех предложенных комбинаций, то у вас готово новое предложение, и вы получите либо успех, либо новые элементы для сравнения.

Если испытание комбинации потерпело неудачу, то вы переходите к следующей, начиная, если это возможно, с последнего, отступая на одну позицию и испытывая следующий цвет на этой самой позиции.

Для экономии вычислений вы можете быть заинтересованы в том, чтобы сохранить некоторые результаты, полученные во время исследования одной позиции за другой. Но внимание! Когда вы возвращаетесь назад, нужно знать, как определить, что нужно сохранить, а что исключить. Используйте при необходимости изучение «гениального ответчика» (игра 6), чтобы выбрать наилучший способ определения белых и черных шашек.

Игра 25.

Как и при игре Сима, невозможно действовать из комбинаторных соображений, т. е. изучать при каждом ходе компьютера все окончания всех возможных партий. Поэтому нужно взвешивать различные ситуации и делать наилучший ход.

Я предоставляю вам выбор весов…

Игра 26.

Все то же самое. У вас 7 игровых положений. Поэтому ваша программа должна пробежаться по 7 столбцам и для каждого из них вычислить вес игрового положения. Ход определяется положением с наибольшим весом. Если есть два положения с одинаковым весом, предпочтительнее более высокое.

Чтобы определить веса игрового положения, нужно видеть, принадлежит ли оно отрезку из четырех игровых положений, уже содержащему 3 ваших шашки (тогда именно так и нужно играть: максимальный вес) или 3 шашки противника (максимальный вес минус 1). Если игровое положение находится на пересечении двух отрезков, содержащих по две шашки противника и ничего больше, то оно представляет очень большой интерес для хода. Продолжите этот анализ, и ваша программа будет носить ваш отличительный знак.

Совершенно ясно, что для каждого игрового положения нужно знать состояние всех проходящих через него отрезков. В этой игре есть 50 различных отрезков с 4 положениями. Выбор ясен:

— либо на каждом ходе вы определяете с помощью программы состояние всех отрезков, проходящих через точку;

— либо у вас есть таблица, задающая состояния всех отрезков. В этом случае нужно обновлять данные после каждого хода.

После всего этого вам нужно сделать еще один выбор. Пусть дано игровое положение, нужно узнать список проходящих через него отрезков;

— либо вы определяете его с помощью программы,

— либо вы его задаете с помощью таблицы. Поскольку она не меняется в течение игры, то эта таблица вычисляется раз и навсегда.

Поскольку одно и то же игровое поле может изучаться несколько раз, то, конечно, более выгодно устроить обращение к таблице. Но вам придется преодолеть две трудности: число отрезков, проходящих через данную точку, не постоянно, но меняется от точки к точке, таблицу очень неприятно распечатывать. Я написал верную программу, но я сделал немало ошибок при наборе таблицы и пришлось их исправлять,..

Остается способ вычисления состояния отрезка. Я принял следующее соглашение:

— поле, ход на которое невозможен, обозначается 0 (нулем);

— поле, ход на которое возможен, обозначается 1.

Так как нужно изучить отрезки, проходящие через игровое поле, то их наименьшее число 1, но может доходить и до 4. Поэтому нужно быть в состоянии выделять среди них сегмент, содержащий игровое поле и шашку +. Следовательно, придадим такой шашке значение 4. Может появиться отрезок, содержащий ·+++ со значением 13, отличающийся от сегмента с игровым полем и шашкой 0.

Поэтому я придаю такой шашке значение 13. В общем, можно взять в качестве значения отрезка сумму значений пометок на этом отрезке. Наконец, нужно задать таблицу, сопоставляющую вес каждому возможному значению отрезка.

В вашу программу входит тогда много данных, но взамен у вас отличное время ответа. Если у вашего компьютера память слишком мала, чтобы иметь возможность сохранить все данные, не храните их и проделывайте вычисления, когда это необходимо. Тогда вы потеряете время на ответ, и выигрыш в пространстве не обязательно будет слишком большим: ведь вы замените данные программой…

Оглавление книги