Книга: Программирование игр и головоломок

2. Игры с числами

2. Игры с числами

Головоломка 3.

Я нашел это упражнение в монографии, посвященной языку Пролог. Предложенное там решение действует методом проб и ошибок. Но задача решается намного проще.

Как всегда, полностью определим задачу. Искомое число представляется в десятичной системе последовательностью цифр

cnc_n?1…c₂5

Умножая на 5, получаем

5cnc_n?1…c₃c₂

Отсюда следует, что c₂ = 5. Все цифры c_i точно так же итеративно вычисляются справа налево, обыгрывая оставшееся от предыдущего умножения «в уме»: когда вы умножаете крайнее справа 5 на 5, вы получаете 5 единиц, что и дает c₂ = 5, и 2 «в уме». Тогда вы можете вычислить c₃ и новую цифру «в уме» и продолжать шаг за шагом. Остается маленькая задача о том, как узнать, когда следует остановиться. Изучите ее сами; как обычно, я не хотел бы сообщать вам все…

Вы можете также действовать слева направо:

5cnc_n?1…c₃c₂ : 5 = cnc_n?1…c₂5

Деля левую цифру на 5, вы получаете cn = 1. Имея cn, вы можете продолжать деление. И здесь тоже вам нужно будет принимать во внимание перенос результата, полученного при предыдущем делении, и нужно будет знать, когда остановиться. Эти два метода по существу равносильны.

Остальное оставляю исследовать вам.

Головоломка 4.

Обычно я бываю глубоко разочарован тем, что нахожу в книгах по информатике или по математике касательно квадратных корней. Чаще всего вам предлагают метод Ньютона: пусть вам нужно извлечь квадратный корень из числа x. Вы образуете возвратную последовательность u_i по правилу

u_i+1 = (u_i + (x/u_i))/2.

Вне всякого сомнения, вы можете взять u₀ = 1 в качестве начального значения. Эта последовательность очень быстро сходится к квадратному корню из x. Если, например, взять x = 50 и воспользоваться формулой

u_i+1 = целая_часть ((u_i + (x/u_i))/2),

чтобы иметь дело только с целыми числами, то в качестве последовательных значений и вы получите

u₀ = 1, u₁ = 25, u₂ = 13, u₃ = 8, u₅ = 7, u₆ = 7.

Чтобы использовать здесь этот алгоритм, вы должны написать программу целочисленного деления двух целых чисел большой длины.

Другой способ действия основан на том факте, что разность двух последовательных квадратов есть нечетное число:

(n + 1)? ? n? = 2n + 1,

так что последовательные разности являются последовательными нечетными числами. Поэтому можно видеть, что сумма нечетных чисел от 1 до 2k ? 1 включительно есть k?. Обратно, если вычитать из n последовательно возрастающие числа, пока это возможно (не допуская, чтобы результат становился отрицательным), тогда искомый квадратный корень есть к, если последнее нечетное вычитаемое равно 2k ? 1. Таким образом, для 50

50 ? 1 = 49,

49 ? 3 = 46,

46 ? 5 = 41,

41 ? 7 = 34,

34 ? 9 = 25,

25 ? 11 = 14,

14 ? 13 = 1.

Нельзя продолжать, не получая отрицательной разности. Последнее нечетное вычитаемое равно 13, поэтому корень есть (13 + 1)/2 = 7 (и остаток 1). Этот способ гораздо лучше подходит для распространения на случай очень больших чисел, потому что вам требуется реализовать только две операции:

— прибавить 2 к большому числу;

— вычесть одно большое число из другого.

Но число шагов цикла равно искомому квадратному корню, а он может оказаться весьма большим.

Можно обобщить предыдущий алгоритм, используя свойства десятичной записи чисел. Данное число разделяется на куски по две цифры, начиная справа; затем мы начинаем вычитать последовательные нечетные числа из крайнего слева куска:

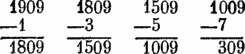
Если это нельзя продолжать дальше, то последнее вычитаемое число увеличивается на единицу, сдвигается на один шаг вправо, и следом за ней приписывается единица. Это — первое нечетное число, которое следует вычитать из предыдущего остатка.

В приведенном выше примере 7 + 1 = 8; приписывая 4, получаем 81 и продолжаем:

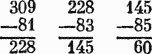
Поскольку продолжать дальше нельзя (последнее возможное вычитание из остатка — это крайнее справа), то последнее из вычитаемых чисел нужно увеличить на 1, а затем разделить на 2, чтобы получить корень. Последний остаток и есть остаток квадратного корня:

85 + 1 = 86, 86/2 = 43,

1909 = (43)² + 60.

Этот алгоритм достаточно прост для программирования при длинных числах, и он дает вполне разумное время вычисления.

У вас много возможностей представлять свои данные. Так как мы оперируем с кусками из двух цифр, то вы можете задавать свои данные таблицами целых чисел в интервале от 0 до 99.

Вы можете представлять свои целые числа как цепочки символов, где используются только числовые символы (цифры) от 0 до 9. Выбор способа зависит от ваших предпочтений и от возможностей вашей машины оперировать с таблицами и цепочками. Тщательно рассмотрите, какие операции нужно сделать. Вы ничем не ограничены: почему бы не запрограммировать и сравнить два разных решения?

Я предложил вам алгоритм без доказательства. Поэтому попытайтесь его проверить…

Я предложил вам алгоритм для десятичной системы счисления. Можно предложить похожий алгоритм для двоичной системы. Тогда не возникнет цикл вычитаний последовательных нечетных чисел из каждого куска, поскольку в куске есть только одно нечетное число: 1. Алгоритм упрощается: если можно вычесть нечетное число — мы его вычитаем, в противном случае мы не делаем ничего. Затем сдвигаем, добавляем 1 и приписываем 1 в конце… Этот алгоритм намного легче реализовать. Но тогда нужно сначала перейти к основанию 2, а затем преобразовать двоичный результат в десятичный. Вам следует посмотреть, что более эффективно…

Головоломка 5.

Аккуратно поставим задачу. То, что от вас требуется, — это не взятая глобально последовательность, а вот что: если начало последовательности выписано, то нужно найти следующее число. Возьмем пример, данный в головоломке 5: какое число следует за 50?

Есть ровно три возможности.

1. Число делится на 2. После однократного деления на 2 оно не будет иметь других делителей нуля, кроме 2, 3 и 5. Следовательно, это число — из последовательности. Так как 50 : 2 = 25, то полученное частное больше, чем 25. Наименьшее число последовательности, большее 25, есть 27. Таким образом, если следующее за 50 число делится на два, то оно равно 2 ? 27 = 54.

2. Оно делится на 3. То же рассуждение. 50 : 3 = 16,7. Первое число последовательности, большее 16,7, есть 18. Если следующее за 50 число делится на 3, то это число равно 3 ? 18 = 54.

3. Оно делится на 5. 50 : 5 = 10. Следующее за 10 равно 12,

5 ? 12 = 60.

Таким образом, у нас 3 кандидата: 54, 54, 60. Наименьшее из этих трех и есть искомое.

Мы получили 54, используя только уже вычисленную часть последовательности Хэмминга.

Я предложил вам идею решения на примере. Вам следует ее обобщить, показать, что это всегда верно, и составить хорошую программу для решения.

Головоломка 6.

Я предлагаю вам начать с образования различных числовых последовательностей, получаемых вычеркиванием чисел. Вот первые из них:

1 : 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

2 : 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35

3 : 5 7 11 13 17 19 23 25 28 31 35 37 41 43 47 49

На этом уровне можно поверить, что появляется возвратное соотношение: во второй последовательности нет четных чисел, в третьей — нет кратных трем. Образуем следующую: 25, кратное 5 содержится. Покажем механизм перехода от одной последовательности к другой последовательности

3 : 5 7 11 13 17 19 23 26 29 31 35 37 41 43 47 49

5 : 7 11 13 17 23 25 29 81 87 41 43 47

Если вы все это хорошо поняли, то вы теперь должны суметь обобщить. Обозначим черев g(i, j) число, стоящее в последовательности ранга i, которая начинается с g(i, 0). Число g(i, 0) = h(i) и есть счастливое число ранга i. Если вы можете построить g(i + 1, j), исходя ив g(i, …), то вы должны суметь решить задачу. Само собою разумеется, что таблица чисел g не должна участвовать в программе. Это — только промежуточное средство вычисления…

Головоломка 7.

Нужно попытаться сгруппировать эффект нескольких последовательных шагов. Нечетное p дает (3p + 1)/2, которое можно еще переписать в виде

3(p + 1)/2 ? 1,

что дает правило: добавить 1,

разделить на 2 и умножить на 3,

уменьшить на 1.

Предположим, что результат нечетен. За операцией «уменьшить на 1» сраву же следует операция «добавить 1», и в результате этих двух операций ничто не меняется. Отсюда следует новое правило:

добавить 1,

пока результат четен, делить его на 2 и умножать его на 3,

уменьшить на 1,

делить на 2, пока это возможно.

Составьте по этому правилу программу и заставьте ее перечислять все величины, полученные таким образом (все они будут нечетны. Заметьте, что только первое число в ряду может оказаться кратным трем).

Если вы замените 3 на m, то второе правило изменяется: пока результат четен, делить его на 2 и умножать его на m.

Вернемся к случаю числа 3. Наше правило можно переписать следующим образом: пусть k — некоторое нечетное число; тогда 2pk ? 1 дает (3pk ? 1)/2^q.

Назовем эту операцию переходом p, q.

Можете ли вы показать, что:

если n = 2 по модулю 3, то элемент, следующий за n, равен некоторому элементу, следующему за (2n ? 1)/3;

если n дает некоторое n при переходе p, q, где q > 1, то число (n ? 1)/2 порождает ту же последовательность, что и n, за исключением, быть может, нескольких первых членов.

Любое число вида n = 4k + 1 имеет непосредственно следующее n' < n.

Для того чтобы n допускало переход p, 1, необходимо и достаточно, чтобы n имело вид n = k2^p ? 1, где

k = 1 по модулю 4, если p нечетно,

k = 3 по модулю 4, если p четно.

Если вы хотите проверить о помощью программы, что это свойство выполняется для любого нечетного n в данном интервале от 3 до n, вы можете пробежать все нечетные числа в возрастающем порядке и проверить, что для каждого ив них это верно. Но вы можете сначала вычеркнуть из списка все нечетные числа, о которых вы знаете, что их поведение сводится к поведению последовательности, относящейся к меньшему нечетному числу, поскольку список нечетных чисел пробегается в возрастающем порядке, и этот случай уже был неучен. Таким образом, остается не больше чисел, чем уже было отмечено.

Но построить список априори, без вычеркиваний в более широком списке, так же трудно, как построить последовательность счастливых чисел…

Затем можно пытаться сделать еще один шаг: для любого не вычеркнутого n вычислить первый следующий за ним элемент. Он больше n (в противном случае n был бы вычеркнут). Если он содержится в интервале от 3 до N, то мы ничего не делаем (этот случай будет изучен ниже). Если же он больше N, то мы помещаем его в резерв. Таким образом, мы получим некоторый список чисел, больших N. Если для каждого числа из этого списка возвратная последовательность достигает 1, то мы сможем доказать, что это свойство выполняется для всех чисел, меньших N, и еще для некоторых других.

Конечно, это не доказывает общей теоремы: для любого n предложенная последовательность достигает 1. Но нужно присоединить к делу новую форму рассуждения, которая потребует серьезных размышлений и надежных логических оснований для того, чтобы оказалось возможным поправить дело…

Вот, наконец, последнее свойство, которое вы должны уметь доказывать: не существует пар p, q, где p и q — натуральные числа, для которых n дает n при переходе p, q. Это не означает, что не существует периодических последовательностей. Про них я сумел доказать только тот факт, что не может иметь места цикл

n дает n' при переходе p, q;

n' дает n при переходе p', q'.

Как бы то ни было, этого на сей раз недостаточно.

Но это полезно, чтобы увидеть, каким образом 3 играет существенную роль в этом деле…

Оглавление книги