Книга: Программирование игр и головоломок

3. Игры без стратегии

3. Игры без стратегии

Игра 6.

Единственная задача: считать белые шашки. На самом деле, черные можно получить, сравнивая шашку на шашкой в тайной комбинации и в комбинации, предложенной игроком.

Для подсчета белых шашек у вас есть много возможностей.

1. Во время подсчета черных шашек удалите из тайной комбинации и из комбинации, предложенной игроком, находящиеся в соответствии элементы (имеющие одинаковые значения и одинаковые места). Затем для каждого из элементов, оставшихся в предложенной комбинации, посмотрите, участвует ли он в тайной комбинации, и если да, то учтите его белой шашкой и удалите его из тайной комбинации.

Этот метод требует, чтобы вы создали копию тайной комбинации, Это стоит не слишком дорого…

2. Для каждого из возможных значений шашек (6, если есть 6 цветов) подсчитайте число шашек этого цвета в тайной комбинации и в предложенной комбинации. Меньшее из этих двух чисел равно сумме белых и черных шашек, отвечающих этому цвету (почему?).

Так как вы нуждаетесь в подсчете по цветам шашек тайной комбинации и так как эти величины не меняются в течение партии, то вам может оказаться полезным сделать этот подсчет до запрашивания первой комбинации игрока, а затем сохранять его в виде таблицы…

Игра 7.

Для программирования нет совершенно никаких трудностей. Действительно, от вас требуется принять только одно решение; как вы представите игру в вашей программе?

У вас много возможностей.

1. Никакого внутреннего представления игры. Скорость движения машин и интервалы между машинами суть постоянные величины, которые вы можете поместить в таблицу или каждый раз пересчитывать.

Вы можете задать себе с помощью маленькой таблицы положение крайней левой машины на каждой строке. Все остальное можно отсюда вывести. Но вам придется проделать немало вычислений к моменту вывода на экран.

2. Можно сохранять каждую строку в памяти в виде цепочки символов (за исключением, быть может, первых символов, крайних слева). Тогда вывод на экран очень прост. Передвижение машин влево можно получить, удаляя заданное число символов в начале цепочки и добавляя столько же символов справа, соблюдая условия правильного расположения стрелок на правильных местах.

Вам не нужно экономить ни время вычисления, ни объем памяти. Выберите решение, которое, как вам кажется, проще всего реализовать…

Игра 8.

Перемещение шадока почти не составляет проблемы: вы читаете данную в ответ цепочку символов. Если она содержит П, то абсцисса шадока увеличивается на 1, и т. д.

Перемещение многочисленных гиби немного более сложно. Для каждого из гиби нужно найти ближайший к нему цветок. Если у вас есть таблица, задающая положения цветов, то вы ее полностью перебираете и отыскиваете ближайший. Если у вас такой таблицы нет, то нужно вертеться кругами вокруг каждого из гиби, чтобы найти ближайший цветок. Первое решение кажется лучшим.

Но если у вас есть таблица цветов, то нужно, по ходу движения гиби, исключать один за другим уже сорванные цветки (как вы собираетесь это сделать?). Здесь есть и некоторое преимущество: цветок может быть сорван только одним из гиби. Как только это произошло, цветок больше не привлекает других гиби. Когда время сбора плодов истекает, вы знаете, сколько цветков исчезло, и вы случайным образом добавляете столько же цветков в игру.

Вам нужно еще решить, сохраняете ли вы в памяти образ игры (например, в форме цепочки символов или таблицы цепочек, по цепочке на каждую строчку, или двумерной таблицы, дающей содержание каждого поля) или же вы сохраняете только координаты активных элементов (шадока, гиби и цветов). Не принимайте решение наугад. Тщательно обдумайте преимущества и неудобства каждого решения как с точки зрения результатов, так и с точки зрения простоты программирования (что должно быть определяющим критерием).

Игра 9.

Мало что можно добавить. Единственная трудность — движение убийц. Они должны стремиться приблизиться к игроку, но это не всегда возможно. Вы легко можете определить направление наилучшего перемещения: это направление, которое уменьшает скачок координат убийцы и игрока. Если такое перемещение возможно, то убийца перемещается. Если оно невозможно, то следует испытать близкие перемещения,

Вот способ действовать: задайте таблицу, определяющую возможные перемещения, помеченные индексами от 1 до 8, Желательное перемещение соответствует некоторому элементу таблицы, скажем, элементу с номером k. Испытаем тогда перемещение k, затем, если оно невозможно, перемещения k ? 1 и k + 1, затем k ? 2 и k + 2… Когда индекс становится нулем, мы его заменяем на 8, Когда он становится больше восьми, мы заменяем его на 1, что сводится к организации таблицы по круговому списку. Внимание, это допустимо только в случае, если вы правильно упорядочили перемещения в таблице…

Как и в предыдущих играх, тщательно продумайте способ представления игры, задайте всю необходимую информацию для упрощения программирования. Не позволяйте себе увлечься оптимизацией времени вычислений или объема требуемой памяти. Эта игра должна легко поместиться на любом микрокомпьютере. Работайте аккуратно: если то, что вы запрограммировали, не удовлетворяет правилам игры, то ваша игра нечестная.

Игра 10.

Добавить нечего. Это проще, чем в случае убийц. Вы определяете направление перемещения, которое наилучшим образом приближает робота к игроку (перемещение, которое уменьшает скачки обеих координат). Вы перемещаете робота в этом направлении. Если он попадает в расщелину, то он исключается из игры. Если он попадает на поле другого робота, то он также исключается. Используйте генератор случайных чисел, чтобы решить, помещаете ли вы в углы новых роботов. Например, если случайное число меньше 0,7, то вы ставите нового робота; в противном случае вы не делаете ничего. Это означает, что есть 7 шансов из 10 увидеть появление нового робота…

Игра 11.

Никаких особенных трудностей, если не считать тех, которые связаны с рисунком дороги и положением препятствий. У вас много способов представить игру. Если вы используете таблицу, то факт перемещения фигуры очевидно обязывает вас производить сдвиги. Если вы используете цепочки символов, то дело упрощается. Вы можете, например, состыковывать (конкатенировать) различные строчки (вначале — пробелы, 4 знака (точка, звездочка, 0), код окончания строки) в единую строку, которую вы выводите на экран кусок за куском. Чтобы сдвинуть фигуру, вы убираете некоторое количество кусков в начале (определяемое скоростью) и добавляете столько же в конце. Но это неприемлемо, если ваш компьютер не допускает длинных цепочек (счастливы обладатели LSE1).

Чтобы заставить дорогу повернуть, вы изменяете на i число пробелов в начале. Но не выбирайте случайным образом одно из трех чисел: ?1, 0, 1. (Технически это легко. Вы выбираете случайным образом число в интервале (0, 1), скажем x, а затем берете целую часть от (3 * x), уменьшенную на 1.) Если вы сделаете так, то дорога останется приблизительно прямой с маленькими колебаниями влево или вправо. Задайте фактор поворота принимающий значения ?1, 0 или 1. На каждой новой строке вы увеличиваете на t число пробелов в начале. Чтобы изменить t, вы выбираете случайное число. Вы надаете постоянную величину a. Если случайное число меньше a, то вы уменьшаете t на 1, и если это действие дает вам ?2, то вы полагаете t равным 1. Если, напротив, случайное число больше, чем 1 ? a, то вы увеличиваете t нa 1 и если получаете 2, то заменяете его на ?1. Параметр a вы подберете экспериментально.

Для размещения тяжелых грузовиков вы можете случайным образом выбирать целое число в интервале длины, большей 4. Если оно примет значения 1, 2, 3 или 4, то вы помещаете грузовик в соответствующий ряд, а если оно примет большее значение, то препятствия нет. Чем больше выбранный исходный интервал, тем меньше шансов для появления грузовика. Подберите этот параметр экспериментально.

Игра 12.

Итак, мы покончили с «маленькими играми». Все предыдущие требовали лишь немного умения программировать и немного ловкости. С другой стороны, они требовали большой тщательности, и только хорошие программисты могли сделать из них что-нибудь красивое и приятное. Ну, а в этой игре, по моему мнению, нужно действовать более мощными методами.

Тщательно проанализируйте способ создания комбинации, исходя из 6 шашек. Начало всегда одно и то же.

Вы выбираете две шашки, скажем a и b, и соединяете их одной из операций:

a + b, a ? b, a * b, a : b.

Сложение возможно всегда. Что касается вычитания, то с ним дела обстоят так же, если договориться, что мы всегда вычитаем меньшее из большего (это относится к правильному наименованию чисел, или — что то же — к взятию той из двух операций a ? b или b — a, которая дает положительный результат). Заметим, однако, что если a = b, то знак «?» выбирать нельзя.

a * b можно вычислять только тогда, когда ни один из двух сомножителей не равен 1.

a : b ориентировано (как и вычитание). Число b не должно быть равно 1. Остаток при делении должен быть нулевым.

Все это не очень трудно запрограммировать. Вы случайным образом выбираете две шашки. Затем вы случайным образом выбираете знак операции, а если его нельзя использовать — вы повторяете розыгрыш знака. В конце концов вы всегда получите хороший знак…

Теперь вы получили промежуточный результат. Вы можете решить остановиться, а затем выбрать случайным образом недостающие шашки, которые не участвовали в счете:

7 * 75 = 525 8 3 1 10;

вы выводите на экран

1 3 7 8 10 75 найдено: 525.

Вы можете выбрать новую шашку и скомбинировать ее с предыдущим результатом

525 ? 8 = 517,

Вы снова получите промежуточный результат.

Вы можете выбрать две шашки и скомбинировать их:

3 * 7 = 21.

Тогда вы получите два промежуточных результата:

7 * 75 = 525; 3 * 7 = 21

Если у вас два промежуточных результата, то появляется много возможностей:

— все 6 шашек уже выбраны. Вы комбинируете между собой два промежуточных результата и получаете вашу окончательную комбинацию;

— даже если не все 6 шашек использованы, вы можете скомбинировать между собой два промежуточных результата и снова получить один-единственный результат.

Но вы можете также выбрать новую шашку и скомбинировать ее с одним из двух промежуточных результатов. Вы снова получите два промежуточных результата.

Таким образом, вы получаете то, что называется конечным автоматом. Есть четыре возможных состояния:

начальное состояние, состояние ОДИН, в котором у вас есть один (и притом единственный) промежуточный результат.

состояние ДВА, в котором у вас есть два промежуточных результата,

конечное состояние, в котором у вас есть результат, который вы рассматриваете как достигнутую цель. В вычислениях участвуют три операции.

Т2: выбрать случайным образом две шашки и соединить их случайным образом выбранным знаком, чтобы получить промежуточный результат;

Т1: случайным образом выбрать шашку и соединить ее случайным знаком с промежуточным результатом;

Т0: соединить два промежуточных результата между собой случайным образом выбранным знаком.

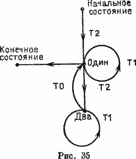
Рисунок 35 дает граф этого автомата, где стрелки показывают операции, которые нужно выполнить, чтобы перейти от одного состояния к другому. Ваша программа должна реализовать этот автомат, причем переходы должны выбираться случайным образом, если это возможно.

Вы теперь знаете все. Конечные автоматы часто встречаются в программировании. Запомните этот пример, он имеет очень широкую область применения…

Игра 13.

Проблема наиболее длинного пути взятия является типичной возвратной задачей. Когда лиса находится в некотором положении, нужно испытать 4 возможных направления и для каждого из них увидеть, есть ли курица и свободно ли следующее за ней поле. Это легко!

Если вы не обнаружили никакого возможного взятия, то все закончено.

Если вы обнаружили возможное взятие, то результат есть наиболее длинное взятие, возможное при этом новом исходном положении, увеличенное на 1.

Но вы можете также действовать итеративным способом. Вы делаете первое взятие и продолжаете дальнейшие исследования, исходя из этого поля прибытия. Нужно испытать все возможности. Вы снова получаете, таким образом, тип задач, известный по головоломке 8. Упорядочьте четыре направления перемещения. Вы исходите из некоторого положения с направлением перемещения i = 1.

Если все четыре направления испытаны, то все закончено.

В противном случае вы смотрите, возможно ли взятие в направлении i:

— если невозможно, то вы увеличиваете i на 1 и возвращаетесь для нового цикла;

— если возможно, то вы выполняете это взятие, оказываетесь в новом положении и начинаете заново, исходя из него.

Внимание: нужно иметь возможность отменять сделанные вами взятия, потому что они происходят в рамках исследования… Это требует некоторой ловкости. По этой причине рассматриваемая игра — не из самых легких.

Остальное вы исследуете совершенно самостоятельно.

Игра 14.

Ничего нового с точки зрения программирования, за исключением того, что нужно исследовать восемь направлений перемещения вместо четырех.

Оглавление книги