Книга: Этюды для программистов
Комментарии к алгоритму Тоома—Кука
Комментарии к алгоритму Тоома—Кука
Мы почти не обосновывали и не объясняли алгоритм; вам придется кое в чем поверить на слово. Причина отсутствия объяснений кроется в том, что они крайне длинны и математичны, и у нас просто не хватило бы места. Изложение алгоритма в большой степени опирается на монографию Кнута; если вы хотите ознакомиться с алгоритмом подробнее, обратитесь к этой книге. Мы все же дадим некоторые комментарии, возможно способствующие лучшему пониманию.
1. (Структура алгоритма.) Наша версия алгоритма отличается от описанной у Кнута в основном структурой циклов. На рис. 22.1 представлена общая схема верхнего уровня алгоритма Тоома—Кука[32].
begin
long integer [n, u], [n, v];
integer K, Q, R, q [0: 10], r [0: 10];
long integer stack C, U, V, W;
control stack code;
integer k, p, s, t, i, j;
long integer X, Y, Z, w;
control A;
Шаг 1;
Шаг 2;
while code не пуст do
while k > 1 do
шаг 5; шаг 6; шаг 7; шаг 8;
end;
шаг 9;
pop code into A; while А = интерполировать do
шаг 11;
for i=1 to 2t do шаг 13;
for i=2t ? 1 downto 1 do шаг 15;
шаг 16;
end;
if A = стоп then return [m, w];
if A = сохранить then шаг 18; else abort;
end; * главного цикла *
end; * алгоритма Тоома—Кука *
Рисунок 22.1. Управляющая схема алгоритма Тоома—Кука.
2. (Таблицы размеров.) Значения массивов, вычисленные на шаге 2, показаны в табл. 22.1; число в колонке nk равно наибольшему числу битов, которое может быть обработано алгоритмом при K = k. Очевидно, что предельное значение 10 для K не является очень серьезным ограничением. При желании этот предел можно повысить.
| Таблица 22.1. Значения q, r и n | |||
| k | qk | rk | nk |
| 0 | 16 | 4 | |
| 1 | 16 | 4 | 32 |
| 2 | 64 | 4 | 80 |
| 3 | 256 | 4 | 320 |
| 4 | 1024 | 8 | 1280 |
| 5 | 8192 | 8 | 9216 |
| 6 | 65536 | 16 | 73728 |
| 7 | 1048576 | 16 | 1114112 |
| 8 | 16777216 | 16 | 17825792 |
| 9 | 268435456 | 32 | 285212672 |
| 10 | 8589934592 | 32 | 8858370038 |
3. (Глубина стеков в первом цикле.) Максимальная глубина стеков U и V на шагах с 5-го по 8-й равна 2(rK?1 + 1). Глубина стека С может возрастать до
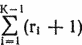
4. (Глубина стеков во втором цикле.) Общая глубина стека W может достигать
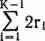
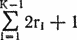
5. (Размер исходных данных.) Для любого числа битов n в диапазоне ni?1 + 1 ? n ? ni алгоритм Тоома—Кука требует одинакового времени вычислений. Таким образом, сложность вычислений весьма негладко зависит от размера исходных данных. Поэтому при выполнении длинных вычислений имеет смысл подбирать число битов вблизи верхнего конца одного из диапазонов для n. Учитывайте, что для представления одной десятичной цифры требуется примерно 3? бита.
6. (Как умножить два 32-разрядных числа?) На шаге 9 требуется умножить два 32-разрядных числа, получив 64-разрядное произведение, причем оба сомножителя обязательно положительны. На многих ЭВМ имеется аппаратная возможность такого умножения, но результат нельзя получить, пользуясь языками высокого уровня. Ну и, конечно, некоторые ЭВМ не имеют подобней аппаратуры. Поэтому для выполнения этого умножения нужно написать подпрограмму, причем она должна быть эффективной, поскольку время работы алгоритма определяется главным образом временем умножения 32-разрядных чисел. Вероятно, достаточно хорошим методом будет разбиение чисел на части и моделирование ручного способа умножения. Тем не менее если нужно получить произведение uv и число и записано в виде u1·216 + u0, a v — в виде v1·216 + v0, то произведением будет
(232 + 216)u1v1 + 216(u1 ? u0)(v0 ? v1) + (216 + 1)u0v0.
Вычисление по этой формуле выполняется при помощи только 16-битовых вычитаний и умножений, а также некоторых сдвигов и сложений. Обратите внимание, что одно умножение сэкономлено.
- Комментарии
- Комментарии (comments)
- 1.2.2. Комментарии и встроенная документация
- Как создавать комментарии к файлам?
- Строки кода и комментарии
- Комментарии в программе
- Комментарии к примеру простой системы "производитель
- Комментарии по поводу реализации объекта порогового барьера
- Комментарии по поводу функций управления очередью с точки зрения производительности
- Комментарии по поводу многоступенчатого конвейера
- Комментарии по поводу клиент-серверного процессора командной строки
- Комментарии по поводу многопоточных моделей




