Книга: Этюды для программистов

8 Тезей, или Автоматическое построение лабиринтов

8

Тезей,

или Автоматическое построение лабиринтов

Тезей должен был найти выход из Критского лабиринта или погибнуть от руки Минотавра. Но что поразительно: найти вход в лабиринт — задача не менее трудная.

Здесь не представляется возможным описать все мыслимые лабиринты, да это и не требуется. Мы займемся простыми лабиринтами, построенными на прямоугольнике m?n, где m, n — положительные целые числа. Внутри и на границах прямоугольника поставлены стенки по ребрам покрывающей его единичной квадратной сетки. Чтобы построить из прямоугольника лабиринт, выбьем одну единичную стенку на одной из сторон прямоугольника (получится вход в лабиринт); выбьем одну единичную стенку на противоположной стороне (получится выход) и еще удалим какое-то число строго внутренних стенок. Говорят, что лабиринт имеет решение, если между входом и выходом внутри лабиринта есть путь в виде ломаной, не имеющей общих точек со стенками. Решение единственно, если любые два таких пути проходят через одни и те же внутренние ячейки сетки. На рис. 8.1 приведен пример лабиринта 6?6.

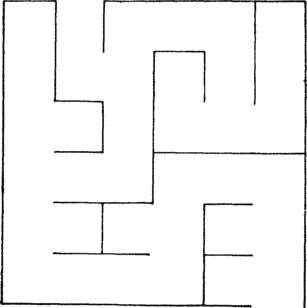
Рисунок 8.1. Пример лабиринта.

Тема. Напишите программу, которая по исходным данным m и n строит прямоугольный лабиринт m?n (проверьте, допустимы ли заданные тип). Предусмотрите, чтобы программа при каждом обращении к ней порождала разные лабиринты. Лабирипг должен иметь единственное решение, и, чтобы получившийся лабиринт был интересным, все ячейки должны быть соединены с основным путем, дающим решение. Если в вашем распоряжении имеется хорошее графическое устройство, используйте его для изображения лабиринтов, в противном случае придумайте систему обозначений для записи лабиринтов или выводите лабиринты на АЦПУ.

Указания исполнителю. Теоретически нельзя удовлетворить требованию, чтобы любые два лабиринта (даже при одинаковых m и n) были различны, поскольку существует лишь конечное число лабиринтов любого наперед заданного размера, а программу можно вызвать большее число раз. Однако число лабиринтов какого-нибудь размера очень велико, и поэтому вероятность повторения лабиринта можно сделать очень маленькой. Практически это достигается, если программа будет производить «случайный» выбор различных вариантов, опираясь на какое-либо доступное ей, но неуправляемое значение (обычно берут дату и время вызова программы). Варианты, между которыми выбирает программа, это, например, положение входа и выхода и положение хотя бы нескольких внутренних разрушаемых стенок. При отладке разумно будет отключить механизм случайного выбора, чтобы изменения результата работы вызывались только изменениями самой программы.

Один из возможных подходов к решению таков. Выбираем вход; затем, начав от него, добавляем по одной ячейке к главному пути-решению, пока он не достигнет выходной стороны. После этого удаляем некоторые внутренние стенки так, чтобы все клетки оказались соединенными с главным путем. Чтобы главный путь не получился прямым коридором, следует при его построении предусмотреть случайные повороты. Программа должна также следить за тем, чтобы при построении главного пути или при открытии боковых ячеек не нарушалась единственность решения. Наблюдательный читатель заметит, что определение единственности решения не годится в случае, когда путь заходит в боковой тупик и затем возвращается. Вы можете попробовать разработать в том же духе формально корректное определение.

Инструментовка. Программу можно написать почти на любом из процедурных языков. Используйте эту программу для сравнения языков с точки зрения управляющих структур, встроенных структур данных и эффективности выполнения.

Длительность исполнения. Одному исполнителю на 3 недели.

Оглавление книги