Книга: Этюды для программистов

Как можно быстро умножать?

Алгоритм быстрого умножения Тоома—Кука, описываемый Кнутом, зиждется на четырех основных идеях[31]. Вот первая из них. Пусть нам известен способ выполнения некоторой операции над исходными данными размера n за время T(n). Если эту операцию удастся разбить на r частей, выполнение каждой из которых займет менее чем T(n)/r шагов, то такое разбиение позволит улучшить общее время, если, конечно, считать, что вспомогательные организационные расходы не сведут экономию на нет. Пусть, далее, каждая из r частей есть применение того же алгоритма к исходным данным длины n/r и каждая часть может быть разбита аналогичным образом. Тогда можно продолжать это разбиение, пока мы не получим столь короткие исходные данные, что вычисления для них станут тривиальными и займут лишь небольшой фиксированный отрезок времени. Этот принцип разделяй и властвуй обычно дает выигрыш во времени работы алгоритма по крайней мере в log n раз; так, классический метод умножения требует времени n?, и его можно свести к

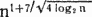
Остальные три идеи касаются чисел и действий над многочленами. Во-первых, заметим, что, если число U имеет длину n битов и записывается в двоичном виде как

u_n?1u_n?2…u₂u₁u₀,

причем n делится на r + 1, то U можно также записать в виде

U_r2^rn/(r+1) + U_r?12^(r?1)n/(r+1) + … + U₁2^n/(r+1) + U₀,

где каждое U_i есть блок из n/(r + 1) битов исходного представления U. Фактически U = U(2^{n/(r + 1)}), где многочлен U(x) есть

U_rx^r + U_r?1x^r?1 + … + U₁x + U₀.

Во-вторых, мы видим, что если U и V — два n-разрядных числа, записанных в виде такого многочлена, то их произведение W дается формулой

W = UV = U(2^{n/(r + 1)})V(2^{n/(r + 1)}) = W(2^{n/(r + 1)})

и если бы мы смогли найти хотя бы коэффициенты W(х), то вычислить W по W было бы сравнительно просто; для этого понадобились бы только сдвиги, сложения и умножения чисел из n/r битов. В-третьих, к счастью, W(х) — многочлен степени 2r и его можно найти с помощью интерполяции его значений в точках 0, 1, 2, …, 2r?1, 2r. Эти значения равны просто U(0), V(0), U(1), V(1), …, U(2r), V(2r). Более того, для вычисления всех этих многочленов и интерполяции требуется умножать числа только из n/r битов. Представляется, что эти действия подпадают под принцип «разделяй и властвуй».

Алгоритм Тоома—Кука весьма сложен, поэтому мы не будем подробно объяснять его; за этим можно обратиться к книге Кнута. Все же необходимо сообщить основные идеи и обозначения. Длинные числа должны быть как-то представлены; будем писать [p, u] для обозначения числа u из p битов. Вероятно, внутреннее представление [p, u] будет некоторой разновидностью списка или цепочки. Кроме основного алгоритма нам понадобятся подпрограммы для сложения и вычитания длинных чисел (используйте стандартный ручной метод сложения слева направо), умножения длинного числа на короткое (небольшое) число, деления длинного числа на короткое, сдвига длинного числа путем приписывания нулей справа и для разбиения длинного числа [p, u] на более короткие длинные числа [p/(r + 1), u_r], [p/(r + 1), u_r?1], …, [p/(r + 1), u₀], как описано выше. Кроме подпрограмм, работающих непосредственно с числами, алгоритм использует четыре стека для хранения промежуточных частичных результатов и несколько временных переменных, поэтому требуются подпрограммы для выполнения некоторых действий над стеком, а также подпрограммы для выделения и освобождения памяти под длинные числа. При написании всяческих вспомогательных подпрограмм черновой работы может оказаться предостаточно.

Оглавление книги